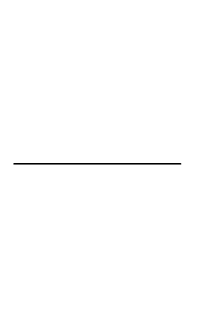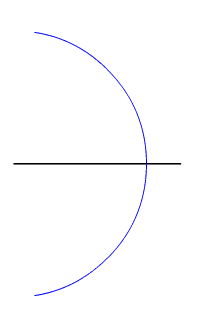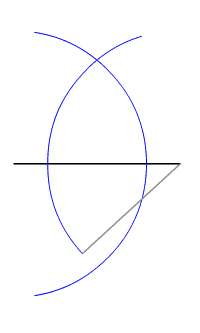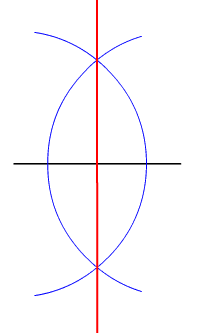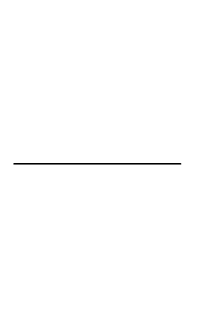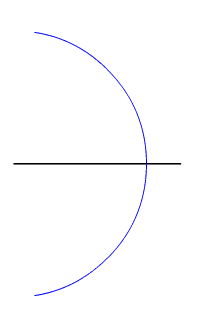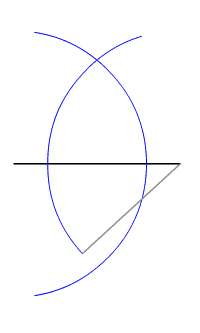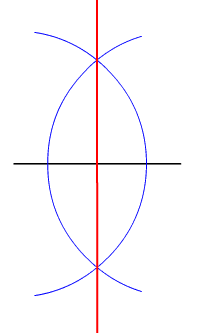A point is said to be equidistant from a set of objects if the

distance Distance is a numerical or occasionally qualitative measurement of how far apart objects or points are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria (e.g. "two counties over"). ...

s between that point and each object in the set are equal. In two-dimensional

Euclidean geometry Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry: the ''Elements''. Euclid's approach consists in assuming a small set of intuitively appealing axioms ...

, the locus of points equidistant from two given (different) points is their

perpendicular bisector In geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a ''bisector''. The most often considered types of bisectors are the ''segment bisector'' (a line that passes through ...

. In three dimensions, the locus of points equidistant from two given points is a plane, and generalising further, in

n-dimensional space In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coordi ...

the locus of points equidistant from two points in ''n''-space is an (''n''−1)-space. For a

triangle A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices ''A'', ''B'', and ''C'' is denoted \triangle ABC. In Euclidean geometry, any three points, when non- colli ...

the circumcentre is a point equidistant from each of the three vertices. Every non-degenerate triangle has such a point. This result can be generalised to

cyclic polygon In geometry, the circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius. Not every polyg ...

s: the circumcentre is equidistant from each of the vertices. Likewise, the incentre of a triangle or any other

tangential polygon In Euclidean geometry, a tangential polygon, also known as a circumscribed polygon, is a convex polygon that contains an inscribed circle (also called an ''incircle''). This is a circle that is tangent to each of the polygon's sides. The dual pol ...

is equidistant from the points of tangency of the polygon's sides with the circle. Every point on a perpendicular bisector of the side of a triangle or other polygon is equidistant from the two vertices at the ends of that side. Every point on the bisector of an angle of any polygon is equidistant from the two sides that emanate from that angle. The center of a rectangle is equidistant from all four vertices, and it is equidistant from two opposite sides and also equidistant from the other two opposite sides. A point on the

axis of symmetry Axial symmetry is symmetry around an axis; an object is axially symmetric if its appearance is unchanged if rotated around an axis.

of a

kite A kite is a tethered heavier than air flight, heavier-than-air or lighter-than-air craft with wing surfaces that react against the air to create Lift (force), lift and Drag (physics), drag forces. A kite consists of wings, tethers and anchors. ...

is equidistant between two sides. The center of a

circle A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is const ...

is equidistant from every point on the circle. Likewise the center of a

sphere A sphere () is a Geometry, geometrical object that is a solid geometry, three-dimensional analogue to a two-dimensional circle. A sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three ...

is equidistant from every point on the sphere. A

parabola In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves. One descri ...

is the set of points in a plane equidistant from a fixed point (the

focus Focus, or its plural form foci may refer to: Arts * Focus or Focus Festival, former name of the Adelaide Fringe arts festival in South Australia Film *''Focus'', a 1962 TV film starring James Whitmore * ''Focus'' (2001 film), a 2001 film based ...

) and a fixed line (the directrix), where distance from the directrix is measured along a line perpendicular to the directrix. In shape analysis, the topological skeleton or medial axis of a

shape A shape or figure is a graphical representation of an object or its external boundary, outline, or external surface, as opposed to other properties such as color, texture, or material type. A plane shape or plane figure is constrained to lie on ...

is a thin version of that shape that is equidistant from its boundaries. In

parallel lines In geometry, parallel lines are coplanar straight lines that do not intersect at any point. Parallel planes are planes in the same three-dimensional space that never meet. '' Parallel curves'' are curves that do not touch each other or inter ...

(lines that never intersect) are equidistant in the sense that the distance of any point on one line from the nearest point on the other line is the same for all points. In

hyperbolic geometry In mathematics, hyperbolic geometry (also called Lobachevskian geometry or Bolyai–Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with: :For any given line ''R'' and point ''P' ...

the set of points that are equidistant from and on one side of a given line form a hypercycle (which is a curve not a line).

References

{{reflist Elementary geometry

See also

References