Energy Cascade on:
[Wikipedia]
[Google]
[Amazon]
 In
In
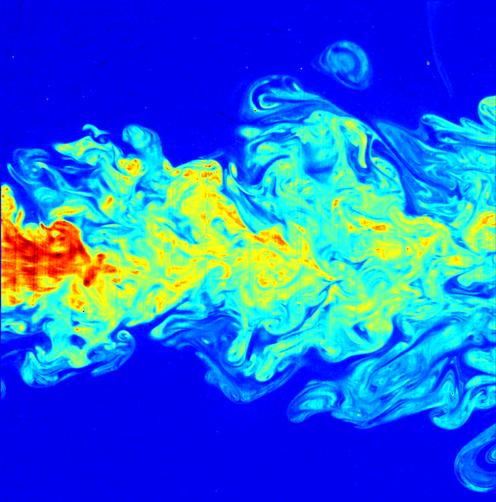
 The largest motions, or eddies, of turbulence contain most of the
The largest motions, or eddies, of turbulence contain most of the
 In
In continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the deformation of and transmission of forces through materials modeled as a ''continuous medium'' (also called a ''continuum'') rather than as discrete particles.
Continuum mec ...
, an energy cascade involves the transfer of energy from large scales of motion to the small scales (called a direct energy cascade) or a transfer of energy from the small scales to the large scales (called an inverse energy cascade). This transfer of energy between different scales requires that the dynamics of the system is nonlinear
In mathematics and science, a nonlinear system (or a non-linear system) is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathe ...
. Strictly speaking, a cascade requires the energy transfer to be local in scale (only between fluctuations of nearly the same size), evoking a cascading waterfall from pool to pool without long-range transfers across the scale domain.
This concept plays an important role in the study of well-developed turbulence
In fluid dynamics, turbulence or turbulent flow is fluid motion characterized by chaotic changes in pressure and flow velocity. It is in contrast to laminar flow, which occurs when a fluid flows in parallel layers with no disruption between ...
. It was memorably expressed in this poem by Lewis F. Richardson in the 1920s. Energy cascades are also important for wind wave
In fluid dynamics, a wind wave, or wind-generated water wave, is a surface wave that occurs on the free surface of bodies of water as a result of the wind blowing over the water's surface. The contact distance in the direction of the wind is ...
s in the theory of wave turbulence.
Consider for instance turbulence generated by the air flow around a tall building: the energy-containing eddies generated by flow separation
In fluid dynamics, flow separation or boundary layer separation is the detachment of a boundary layer from a surface into a wake.
A boundary layer exists whenever there is relative movement between a fluid and a solid surface with viscous fo ...
have sizes of the order of tens of meters. Somewhere downstream, dissipation
In thermodynamics, dissipation is the result of an irreversible process that affects a thermodynamic system. In a dissipative process, energy ( internal, bulk flow kinetic, or system potential) transforms from an initial form to a final form, wh ...
by viscosity
Viscosity is a measure of a fluid's rate-dependent drag (physics), resistance to a change in shape or to movement of its neighboring portions relative to one another. For liquids, it corresponds to the informal concept of ''thickness''; for e ...
takes place, for the most part, in eddies
In fluid dynamics, an eddy is the swirling of a fluid and the reverse current created when the fluid is in a turbulent flow regime. The moving fluid creates a space devoid of downstream-flowing fluid on the downstream side of the object. Fluid ...
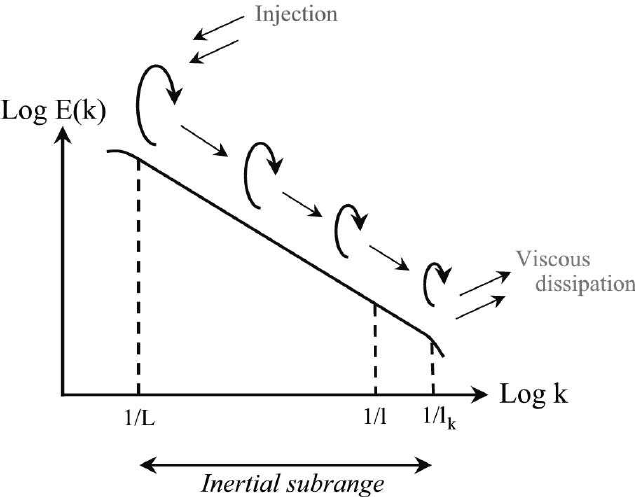
at the Kolmogorov microscales: of the order of a millimetre for the present case. At these intermediate scales, there is neither a direct forcing of the flow nor a significant amount of viscous dissipation, but there is a net nonlinear transfer of energy from the large scales to the small scales.
This intermediate range of scales, if present, is called the inertial subrange. The dynamics at these scales is described by use of self-similarity
In mathematics, a self-similar object is exactly or approximately similar to a part of itself (i.e., the whole has the same shape as one or more of the parts). Many objects in the real world, such as coastlines, are statistically self-similar ...
, or by assumptions – for turbulence closure – on the statistical
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a s ...
properties of the flow in the inertial subrange. A pioneering work was the deduction by Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov ( rus, Андре́й Никола́евич Колмого́ров, p=ɐnˈdrʲej nʲɪkɐˈlajɪvʲɪtɕ kəlmɐˈɡorəf, a=Ru-Andrey Nikolaevich Kolmogorov.ogg, 25 April 1903 – 20 October 1987) was a Soviet ...
in the 1940s of the expected wavenumber
In the physical sciences, the wavenumber (or wave number), also known as repetency, is the spatial frequency of a wave. Ordinary wavenumber is defined as the number of wave cycles divided by length; it is a physical quantity with dimension of ...
spectrum in the turbulence inertial subrange.
Spectra in the inertial subrange of turbulent flow
 The largest motions, or eddies, of turbulence contain most of the
The largest motions, or eddies, of turbulence contain most of the kinetic energy
In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion.
In classical mechanics, the kinetic energy of a non-rotating object of mass ''m'' traveling at a speed ''v'' is \fracmv^2.Resnick, Rober ...
, whereas the smallest eddies are responsible for the viscous dissipation of turbulence kinetic energy. Kolmogorov hypothesized that when these scales are well separated, the intermediate range of length scales would be statistically isotropic, and that its characteristics in equilibrium would depend only on the rate at which kinetic energy is dissipated at the small scales. Dissipation is the friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and material elements sliding against each other. Types of friction include dry, fluid, lubricated, skin, and internal -- an incomplete list. The study of t ...
al conversion of mechanical energy
In physical sciences, mechanical energy is the sum of macroscopic potential and kinetic energies. The principle of conservation of mechanical energy states that if an isolated system is subject only to conservative forces, then the mechanical ...
to thermal energy
The term "thermal energy" is often used ambiguously in physics and engineering. It can denote several different physical concepts, including:
* Internal energy: The energy contained within a body of matter or radiation, excluding the potential en ...
. The dissipation rate, , may be written down in terms of the fluctuating rates of strain in the turbulent flow and the fluid's kinematic viscosity, . It has dimensions of energy per unit mass per second. In equilibrium, the production of turbulence kinetic energy at the large scales of motion is equal to the dissipation of this energy at the small scales.
Energy spectrum of turbulence
The energy spectrum of turbulence, ''E''(''k''), is related to the mean turbulence kinetic energy per unit mass as : where ''u''''i'' are the components of the fluctuating velocity, the overbar denotes an ensemble average, summation over ''i'' is implied, and ''k'' is thewavenumber
In the physical sciences, the wavenumber (or wave number), also known as repetency, is the spatial frequency of a wave. Ordinary wavenumber is defined as the number of wave cycles divided by length; it is a physical quantity with dimension of ...
. The energy spectrum, ''E''(''k''), thus represents the contribution to turbulence kinetic energy by wavenumbers from ''k'' to ''k'' + d''k''. The largest eddies have low wavenumber, and the small eddies have high wavenumbers.
Since diffusion goes as the Laplacian
In mathematics, the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a scalar function on Euclidean space. It is usually denoted by the symbols \nabla\cdot\nabla, \nabla^2 (where \nabla is th ...
of velocity, the dissipation rate may be written in terms of the energy spectrum as:
:
with ν the kinematic viscosity
Viscosity is a measure of a fluid's rate-dependent drag (physics), resistance to a change in shape or to movement of its neighboring portions relative to one another. For liquids, it corresponds to the informal concept of ''thickness''; for e ...
of the fluid. From this equation, it may again be observed that dissipation is mainly associated with high wavenumbers (small eddies) even though kinetic energy is associated mainly with lower wavenumbers (large eddies).
Energy spectrum in the inertial subrange
The transfer of energy from the low wavenumbers to the high wavenumbers is the energy cascade. This transfer brings turbulence kinetic energy from the large scales to the small scales, at which viscous friction dissipates it. In the intermediate range of scales, the so-called inertial subrange, Kolmogorov's hypotheses lead to the following universal form for the energy spectrum: : An extensive body of experimental evidence supports this result, over a vast range of conditions. Experimentally, the value is observed. The result was first stated by independently by Alexander Obukhov in 1941. Obukhov's result is equivalent to a Fourier transform of Kolmogorov's 1941 result for the turbulent structure function.Spectrum of pressure fluctuations
The pressure fluctuations in a turbulent flow may be similarly characterized. The mean-square pressure fluctuation in a turbulent flow may be represented by a pressure spectrum, (''k''): : For the case of turbulence with no mean velocity gradient (isotropic turbulence), the spectrum in the inertial subrange is given by : where ''ρ'' is the fluid density, and ''α'' = 1.32 ''C''2 = 2.97. A mean-flow velocity gradient (shear flow
In solid mechanics, shear flow is the shear stress over a distance in a thin-walled structure.Higdon, Ohlsen, Stiles and Weese (1960), ''Mechanics of Materials'', article 4-9 (2nd edition), John Wiley & Sons, Inc., New York. Library of Congress CCN ...
) creates an additional, additive contribution to the inertial subrange pressure spectrum which varies as ''k''−11/3; but the ''k''−7/3 behavior is dominant at higher wavenumbers.
Spectrum of turbulence-driven disturbances at a free liquid surface
Pressure fluctuations below the free surface of a liquid can drive fluctuating displacements of the liquid surface, which at small wavelengths are modulated by surface tension. This free-surface–turbulence interaction may also be characterized by awavenumber
In the physical sciences, the wavenumber (or wave number), also known as repetency, is the spatial frequency of a wave. Ordinary wavenumber is defined as the number of wave cycles divided by length; it is a physical quantity with dimension of ...
spectrum. If ''δ'' is the instantaneous displacement of the surface from its average position, the mean squared displacement may be represented with a displacement spectrum ''G''(''k'') as:
:
A three dimensional form of the pressure spectrum may be combined with the Young–Laplace equation
In physics, the Young–Laplace equation () is an equation that describes the capillary pressure difference sustained across the interface between two static fluids, such as water and air, due to the phenomenon of surface tension or wall tensi ...
to show that:
:
Experimental observation of this ''k''−19/3 law has been obtained by optical measurements of the surface of turbulent free liquid jets.
Notes
References
* * * * *External links
* {{ scholarpedia , title = Cascade and scaling , curator = G. Falkovich , urlname = Cascade_and_scaling Turbulence Water waves