Elongated Square Dipyramid

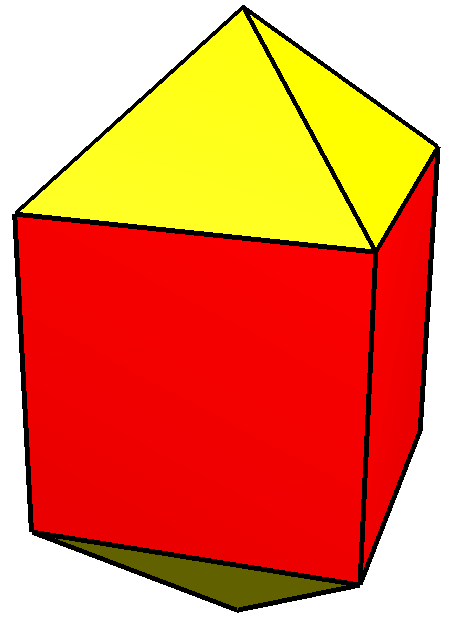
In geometry, the elongated square bipyramid (or elongated octahedron) is the polyhedron constructed by attaching two equilateral square pyramids onto a cube's faces that are opposite each other. It can also be seen as 4 lunes (squares with triangles on opposite sides) linked together with squares to squares and triangles to triangles. It is also been named the pencil cube or 12-faced pencil cube due to its shape.

A zircon crystal is an example of an elongated square bipyramid.

Construction

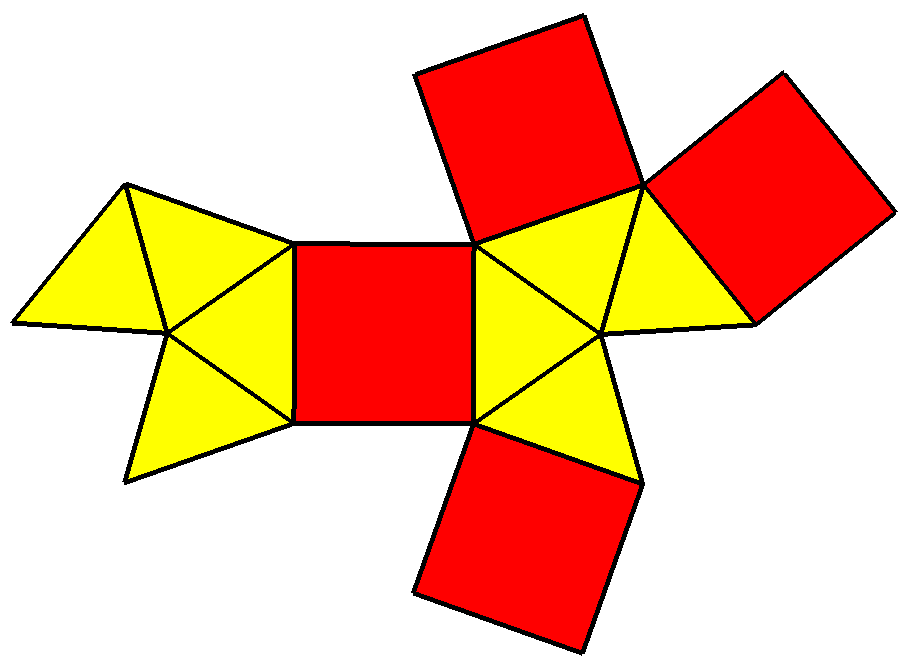
The elongated square bipyramid is constructed by attaching two equilateral square pyramids onto the faces of a cube that are opposite each other, a process known as elongation. This construction involves the removal of those two squares and replacing them with those pyramids, resulting in eight equilateral triangles and four squares as their faces.. A convex polyhedron in which all of its faces are regular is a Johnson solid, and the elongated square bipyramid is one of them, denoted as $J_$, the fifteenth Johnson solid.

Properties

Given that $a$ is the edge length of an elongated square bipyramid. The height of an elongated square pyramid can be calculated by adding the height of two equilateral square pyramids and a cube. The height of a cube is the same as the given edge length $a$, and the height of an equilateral square pyramid is $(1/\sqrt)a$. Therefore, the height of an elongated square bipyramid is:
$a + 2 \cdot \fraca = \left(1 + \sqrt\right)a \approx 2.414a.$
Its surface area can be calculated by adding all the area of eight equilateral triangles and four squares:
$\left(4 + 2\sqrt\right)a^2 \approx 7.464a^2.$
Its volume is obtained by slicing it into two equilateral square pyramids and a cube, and then adding them:
$\left(1 + \frac\right)a^3 \approx 1.471a^3.$
Its dihedral angle can be obtained in a similar way as the elongated square pyramid, by adding the angle of square pyramids and a cube:
* The dihedral angle of an elongated square bipyramid between two adjacent triangles is the dihedral angle of an equilateral triangle between its lateral faces, $\arccos(-1/3) \approx 109.47^\circ$
* The dihedral angle of an elongated square bipyramid between two adjacent squares is the dihedral angle of a cube between those, $\pi/2$
* The dihedral angle of an equilateral square pyramid between square and triangle is $\arctan \left(\sqrt\right) \approx 54.74^\circ$. Therefore, the dihedral angle of an elongated square bipyramid between triangle-to-square, on the edge where the equilateral square pyramids attach the cube, is $\arctan\left(\sqrt\right) + \frac \approx 144.74^\circ.$

The elongated square bipyramid has the dihedral symmetry, the dihedral group $D_$ of order eight: it has an axis of symmetry passing through the apices of square pyramids and the center of a cube, and its appearance is symmetrical by reflecting across a horizontal plane. It is symmetrical by reflecting over three mutually orthogonal planes.

Related polyhedra and honeycombs

The elongated square bipyramid is dual to the square bifrustum, which has eight trapezoidals and two squares.

A special kind of elongated square bipyramid ''without'' all regular faces allows a self-tessellation of Euclidean space. The triangles of this elongated square bipyramid are ''not'' regular; they have edges in the ratio 2::.
:

It can be considered a transitional phase between the cubic and rhombic dodecahedral honeycombs. Here, the cells are colored white, red, and blue based on their orientation in space. The square pyramid ''caps'' have shortened isosceles triangle faces, with six of these pyramids meeting together to form a cube. The dual of this honeycomb is composed of two kinds of octahedra (regular octahedra and triangular antiprisms), formed by superimposing octahedra into the cuboctahedra of the rectified cubic honeycomb. Both honeycombs have a symmetry of ,3,4.

Cross-sections of the honeycomb, through cell centers, produce a chamfered square tiling, with flattened horizontal and vertical hexagons, and squares on the perpendicular polyhedra.

With regular faces, the elongated square bipyramid can form a tessellation of space with tetrahedra and octahedra. (The octahedra can be further decomposed into square pyramids.) This honeycomb can be considered an elongated version of the tetrahedral-octahedral honeycomb.

References

External links

*

{{Johnson solids navigator

Johnson solids
Bipyramids