elongated dodecahedron on:
[Wikipedia]
[Google]
[Amazon]
 In
In Fedorov's five parallelohedra in R³
/ref> is a convex
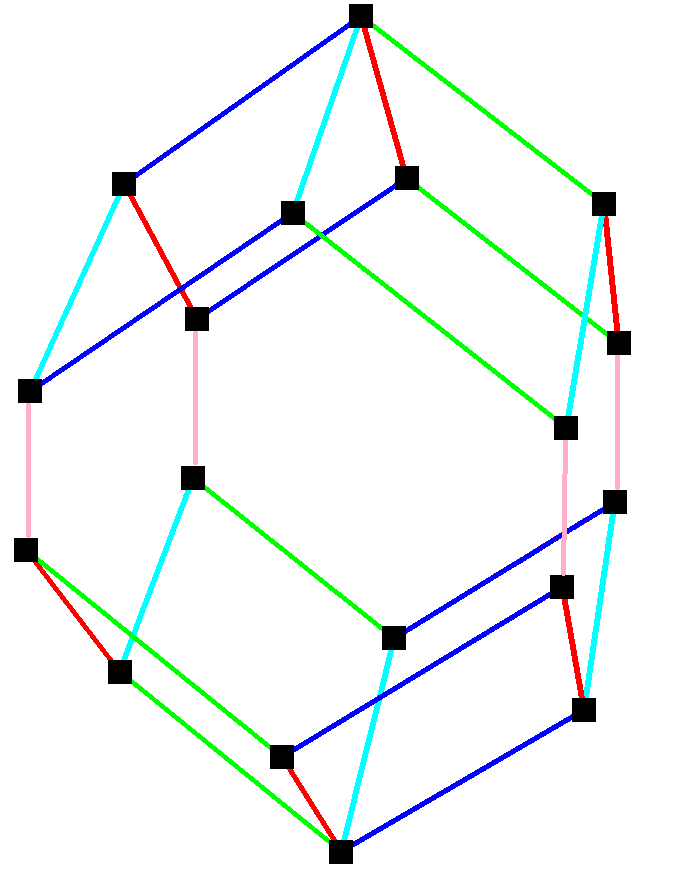
Uniform space-filling using only rhombo-hexagonal dodecahedra
Elongated dodecahedron
VRML Model Space-filling polyhedra Zonohedra
geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, the elongated dodecahedron, extended rhombic dodecahedron, rhombo-hexagonal dodecahedron or hexarhombic dodecahedron/ref> is a convex
dodecahedron
In geometry, a dodecahedron (; ) or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three Kepler–Po ...
with 8 rhombic and 4 hexagon
In geometry, a hexagon (from Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.
Regular hexagon
A regular hexagon is de ...
al faces. The hexagons can be made equilateral, or regular depending on the shape of the rhombi. It can be seen as constructed from a rhombic dodecahedron
In geometry, the rhombic dodecahedron is a Polyhedron#Convex_polyhedra, convex polyhedron with 12 congruence (geometry), congruent rhombus, rhombic face (geometry), faces. It has 24 edge (geometry), edges, and 14 vertex (geometry), vertices of 2 ...
elongated by a square prism.Parallelohedron
Along with the rhombic dodecahedron, it is aspace-filling polyhedron
In geometry, a space-filling polyhedron is a polyhedron that can be used to fill all of three-dimensional space via translations, rotations and/or reflections, where ''filling'' means that; taken together, all the instances of the polyhedron c ...
, one of the five types of parallelohedron
In geometry, a parallelohedron or Fedorov polyhedron is a convex polyhedron that can be Translation (geometry), translated without rotations to fill Euclidean space, producing a Honeycomb (geometry), honeycomb in which all copies of the polyhed ...
identified by Evgraf Fedorov
Evgraf Stepanovich Fedorov (, – 21 May 1919) was a Russian mathematician, crystallographer and mineralogist.
Fedorov was born in the Russian city of Orenburg. His father was a topographical engineer. The family later moved to Saint Petersb ...
that tile space face-to-face by translations. It has 5 sets of parallel edges, called zones or belts.
: 
Tessellation
* It cantesselate
A tessellation or tiling is the covering of a surface, often a plane (mathematics), plane, using one or more geometric shapes, called ''tiles'', with no overlaps and no gaps. In mathematics, tessellation can be generalized to high-dimensiona ...
all space by translations.
* It is the Wigner–Seitz cell for certain body-centered tetragonal lattices.
This is related to the rhombic dodecahedral honeycomb with an elongation of zero. Projected normal to the elongation direction, the honeycomb looks like a square tiling
In geometry, the square tiling, square tessellation or square grid is a regular tiling of the Euclidean plane consisting of four squares around every vertex. John Horton Conway called it a quadrille.
Structure and properties
The square tili ...
with the rhombi
In plane Euclidean geometry, a rhombus (: rhombi or rhombuses) is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The rhom ...
projected into square
In geometry, a square is a regular polygon, regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal si ...
s.
Variations
The expanded dodecahedra can be distorted into cubic volumes, with the honeycomb as a half-offset stacking of cubes. It can also be made concave by adjusting the 8 corners downward by the same amount as the centers are moved up. The elongated dodecahedron can be constructed as a contraction of a uniformtruncated octahedron
In geometry, the truncated octahedron is the Archimedean solid that arises from a regular octahedron by removing six pyramids, one at each of the octahedron's vertices. The truncated octahedron has 14 faces (8 regular hexagon, hexagons and 6 Squa ...
, where square faces are reduced to single edges and regular hexagonal faces are reduced to 60 degree rhombic faces (or pairs of equilateral triangles). This construction alternates square and rhombi on the 4-valence vertices, and has half the symmetry, D2h symmetry, order 8.
See also
* Trapezo-rhombic dodecahedron *Elongated gyrobifastigium
In geometry, the elongated gyrobifastigium or gabled rhombohedron is a space-filling octahedron with 4 rectangles and 4 right-angled pentagonal faces.
Name
The first name is from the regular-faced gyrobifastigium but Elongation (geometry), elon ...
References
* ''rhombo-hexagonal dodecahedron'', p169 * H.S.M. Coxeter, ''Regular Polytopes'', Third edition, (1973), Dover edition, p. 257External links
* * {{mathworld , urlname = ElongatedDodecahedron , title = Elongated dodecahedronUniform space-filling using only rhombo-hexagonal dodecahedra
Elongated dodecahedron
VRML Model Space-filling polyhedra Zonohedra