Elastic pendulum on:
[Wikipedia]
[Google]
[Amazon]
In
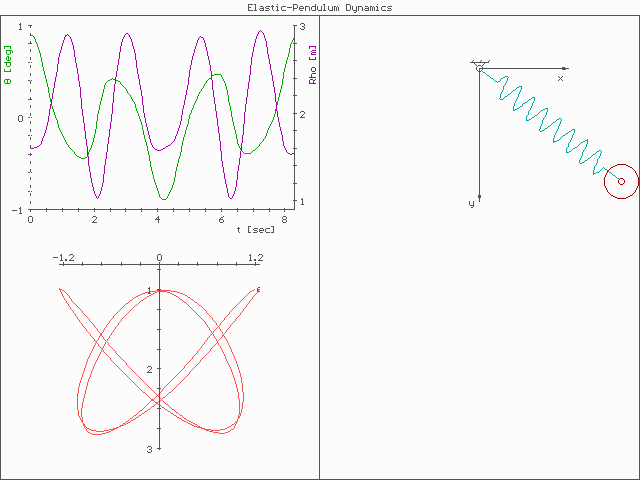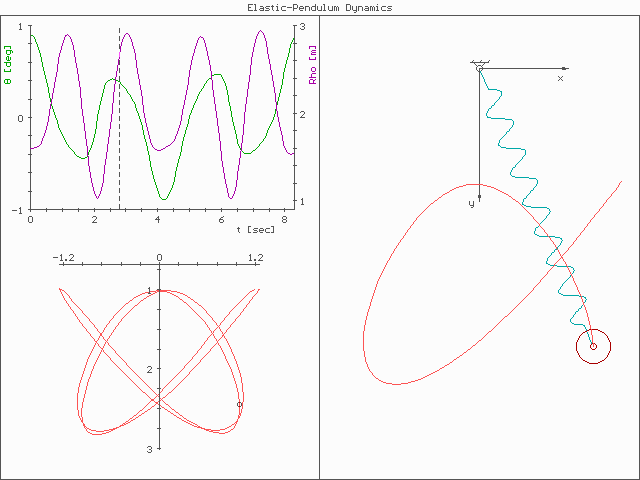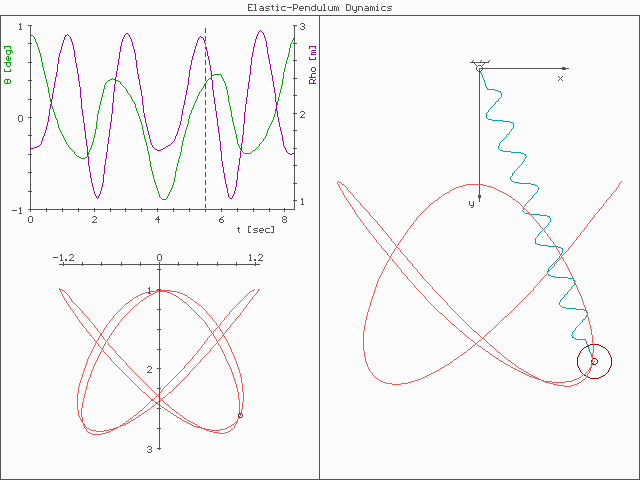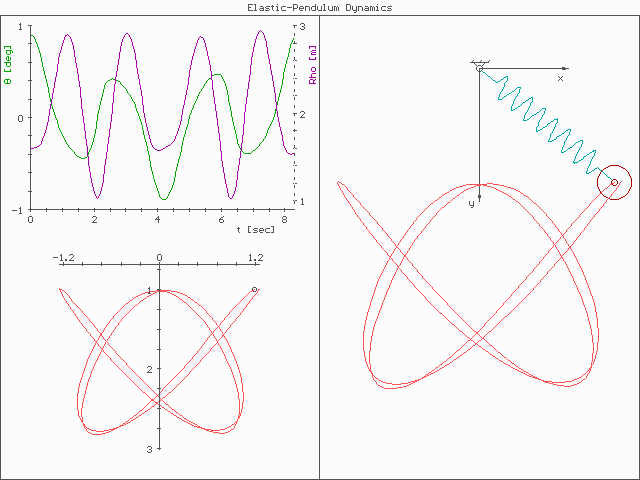 The system is much more complex than a simple pendulum, as the properties of the spring add an extra dimension of freedom to the system. For example, when the spring compresses, the shorter radius causes the spring to move faster due to the conservation of
The system is much more complex than a simple pendulum, as the properties of the spring add an extra dimension of freedom to the system. For example, when the spring compresses, the shorter radius causes the spring to move faster due to the conservation of
"Oscillations of an elastic pendulum"
(interactive animation), Wolfram Demonstrations Project, published February 19, 2019. * Holovatsky V., Holovatskyi I., Holovatska Ya., Struk Ya. Oscillations of the resonant elastic pendulum. Physics and Educational Technology, 2023, 1, 10–17, https://doi.org/10.32782/pet-2023-1-2 http://journals.vnu.volyn.ua/index.php/physics/article/view/1093 {{Chaos theory Chaotic maps Dynamical systems Mathematical physics Pendulums
physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
and mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, in the area of dynamical systems
In mathematics, a dynamical system is a system in which a Function (mathematics), function describes the time dependence of a Point (geometry), point in an ambient space, such as in a parametric curve. Examples include the mathematical models ...
, an elastic pendulum (also called spring pendulum or swinging spring) is a physical system
A physical system is a collection of physical objects under study. The collection differs from a set: all the objects must coexist and have some physical relationship.
In other words, it is a portion of the physical universe chosen for analys ...
where a piece of mass is connected to a spring so that the resulting motion contains elements of both a simple pendulum
A pendulum is a device made of a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate i ...
and a one-dimensional spring-mass system. For specific energy values, the system demonstrates all the hallmarks of chaotic behavior and is sensitive to initial conditions
In mathematics and particularly in dynamic systems, an initial condition, in some contexts called a seed value, is a value of an evolving variable at some point in time designated as the initial time (typically denoted ''t'' = 0). Fo ...
.At very low and very high energy
Energy () is the physical quantity, quantitative physical property, property that is transferred to a physical body, body or to a physical system, recognizable in the performance of Work (thermodynamics), work and in the form of heat and l ...
, there also appears to be regular motion. The motion of an elastic pendulum is governed by a set of coupled ordinary differential equation
In mathematics, an ordinary differential equation (ODE) is a differential equation (DE) dependent on only a single independent variable (mathematics), variable. As with any other DE, its unknown(s) consists of one (or more) Function (mathematic ...
s.This behavior suggests a complex interplay between energy states and system dynamics
System dynamics (SD) is an approach to understanding the nonlinear behaviour of complex systems over time using stocks, flows, internal feedback loops, table functions and time delays.
Overview
System dynamics is a methodology and mathematical ...
.
Analysis and interpretation
 The system is much more complex than a simple pendulum, as the properties of the spring add an extra dimension of freedom to the system. For example, when the spring compresses, the shorter radius causes the spring to move faster due to the conservation of
The system is much more complex than a simple pendulum, as the properties of the spring add an extra dimension of freedom to the system. For example, when the spring compresses, the shorter radius causes the spring to move faster due to the conservation of angular momentum
Angular momentum (sometimes called moment of momentum or rotational momentum) is the rotational analog of Momentum, linear momentum. It is an important physical quantity because it is a Conservation law, conserved quantity – the total ang ...
. It is also possible that the spring has a range that is overtaken by the motion of the pendulum, making it practically neutral to the motion of the pendulum.
Lagrangian
The spring has the rest length and can be stretched by a length . The angle of oscillation of the pendulum is . The Lagrangian is: : where is thekinetic energy
In physics, the kinetic energy of an object is the form of energy that it possesses due to its motion.
In classical mechanics, the kinetic energy of a non-rotating object of mass ''m'' traveling at a speed ''v'' is \fracmv^2.Resnick, Rober ...
and is the potential energy
In physics, potential energy is the energy of an object or system due to the body's position relative to other objects, or the configuration of its particles. The energy is equal to the work done against any restoring forces, such as gravity ...
.
Hooke's law
In physics, Hooke's law is an empirical law which states that the force () needed to extend or compress a spring by some distance () scales linearly with respect to that distance—that is, where is a constant factor characteristic of ...
is the potential energy of the spring itself:
:
where is the spring constant.
The potential energy from gravity
In physics, gravity (), also known as gravitation or a gravitational interaction, is a fundamental interaction, a mutual attraction between all massive particles. On Earth, gravity takes a slightly different meaning: the observed force b ...
, on the other hand, is determined by the height of the mass. For a given angle and displacement, the potential energy is:
:
where is the gravitational acceleration
In physics, gravitational acceleration is the acceleration of an object in free fall within a vacuum (and thus without experiencing drag (physics), drag). This is the steady gain in speed caused exclusively by gravitational attraction. All bodi ...
.
The kinetic energy is given by:
:
where is the velocity
Velocity is a measurement of speed in a certain direction of motion. It is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of physical objects. Velocity is a vector (geometry), vector Physical q ...
of the mass. To relate to the other variables, the velocity is written as a combination of a movement along and perpendicular to the spring:
:
So the Lagrangian becomes:
:
:
Equations of motion
With twodegrees of freedom
In many scientific fields, the degrees of freedom of a system is the number of parameters of the system that may vary independently. For example, a point in the plane has two degrees of freedom for translation: its two coordinates; a non-infinite ...
, for and , the equations of motion can be found using two Euler-Lagrange equations:
:
:
For :
:
isolated:
:
And for :
:
isolated:
:
These can be further simplified by scaling length and time . Expressing the system in terms of and results in nondimensional
Dimensionless quantities, or quantities of dimension one, are quantities implicitly defined in a manner that prevents their aggregation into unit of measurement, units of measurement. ISBN 978-92-822-2272-0. Typically expressed as ratios that a ...
equations of motion. The one remaining dimensionless parameter characterizes the system.
:
:
The elastic pendulum is now described with two coupled ordinary differential equations
In mathematics, an ordinary differential equation (ODE) is a differential equation (DE) dependent on only a single independent variable. As with any other DE, its unknown(s) consists of one (or more) function(s) and involves the derivatives ...
. These can be solved numerically. Furthermore, one can use analytical methods to study the intriguing phenomenon of order-chaos-order in this system for various values of the parameter and initial conditions and .
There is also a second example : Double Elastic Pendulum . See
See also
*Double pendulum
In physics and mathematics, in the area of dynamical systems, a double pendulum, also known as a chaotic pendulum, is a pendulum with another pendulum attached to its end, forming a simple physical system that exhibits rich dynamical systems, dy ...
* Duffing oscillator
* Pendulum (mathematics)
A pendulum is a body suspended from a fixed support such that it freely swings back and forth under the influence of gravity. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to ...
* Spring-mass system
References
Further reading
* *External links
* Holovatsky V., Holovatska Y. (2019"Oscillations of an elastic pendulum"
(interactive animation), Wolfram Demonstrations Project, published February 19, 2019. * Holovatsky V., Holovatskyi I., Holovatska Ya., Struk Ya. Oscillations of the resonant elastic pendulum. Physics and Educational Technology, 2023, 1, 10–17, https://doi.org/10.32782/pet-2023-1-2 http://journals.vnu.volyn.ua/index.php/physics/article/view/1093 {{Chaos theory Chaotic maps Dynamical systems Mathematical physics Pendulums