Elastic Map

Elastic maps provide a tool for nonlinear dimensionality reduction. By their construction, they are a system of elastic springs embedded in the data
space. This system approximates a low-dimensional manifold. The elastic coefficients of this system allow the switch from completely unstructured k-means clustering (zero elasticity) to the estimators located closely to linear PCA manifolds (for high bending and low stretching modules). With some intermediate values of the elasticity coefficients, this system effectively approximates non-linear principal manifolds. This approach is based on a mechanical analogy between principal manifolds, that are passing through "the middle" of the data distribution, and elastic membranes and plates. The method was developed by A.N. Gorban
A.Y. Zinovyev
and A.A. Pitenko in 1996–1998.

Energy of elastic map

Let $$ be a data set in a finite-dimensional Euclidean space. Elastic map is represented by a set of nodes $_j$ in the same space. Each datapoint $s \in$ has a ''host node'', namely the closest node $_j$ (if there are several closest nodes then one takes the node with the smallest number). The data set $$ is divided into classes $K_j=\$.

The ''approximation energy'' D is the distortion
: $D=\frac\sum_^k \sum_\, s-_j\, ^2$,
which is the energy of the springs with unit elasticity which connect each data point with its host node. It is possible to apply weighting factors to the terms of this sum, for example to reflect the standard deviation of the probability density function of any subset of data points $\$.

On the set of nodes an additional structure is defined. Some pairs of nodes, $(_i,_j)$, are connected by ''elastic edges''. Call this set of pairs $E$. Some triplets of nodes, $(_i,_j,_k)$, form ''bending ribs''. Call this set of triplets $G$.
: The stretching energy is $U_=\frac\lambda \sum_ \, _i -_j\, ^2$,
: The bending energy is $U_G=\frac\mu \sum_ \, _i -2_j+_k\, ^2$,
where $\lambda$ and $\mu$ are the stretching and bending moduli respectively. The stretching energy is sometimes referred to as the ''membrane'', while the bending energy is referred to as the ''thin plate'' term.

For example, on the 2D rectangular grid the elastic edges are just vertical and horizontal edges (pairs of closest vertices) and the bending ribs are the vertical or horizontal triplets of consecutive (closest) vertices.
: The total energy of the elastic map is thus $U=D+U_E+U_G.$
The position of the nodes $\$ is determined by the mechanical equilibrium of the elastic map, i.e. its location is such that it minimizes the total energy $U$.

Expectation-maximization algorithm

For a given splitting of dataset $$ in classes $K_j$, minimization of the quadratic functional $U$ is a linear problem with the sparse matrix of coefficients. Therefore, similar to principal component analysis or k-means, a splitting method is used:
* For given $\$ find $\$;
* For given $\$ minimize $U$ and find $\$;
* If no change, terminate.

This expectation-maximization algorithm guarantees a local minimum of $U$. For improving the approximation various additional methods are proposed. For example, the ''softening'' strategy is used. This strategy
starts with a rigid grids (small length, small bending and large elasticity modules
$\lambda$ and $\mu$ coefficients) and finishes with soft grids (small $\lambda$ and $\mu$). The training goes in several epochs, each epoch with its own grid rigidness. Another adaptive strategy is ''growing net'': one starts from a small number of nodes and gradually adds new nodes. Each epoch goes with its own number of nodes.

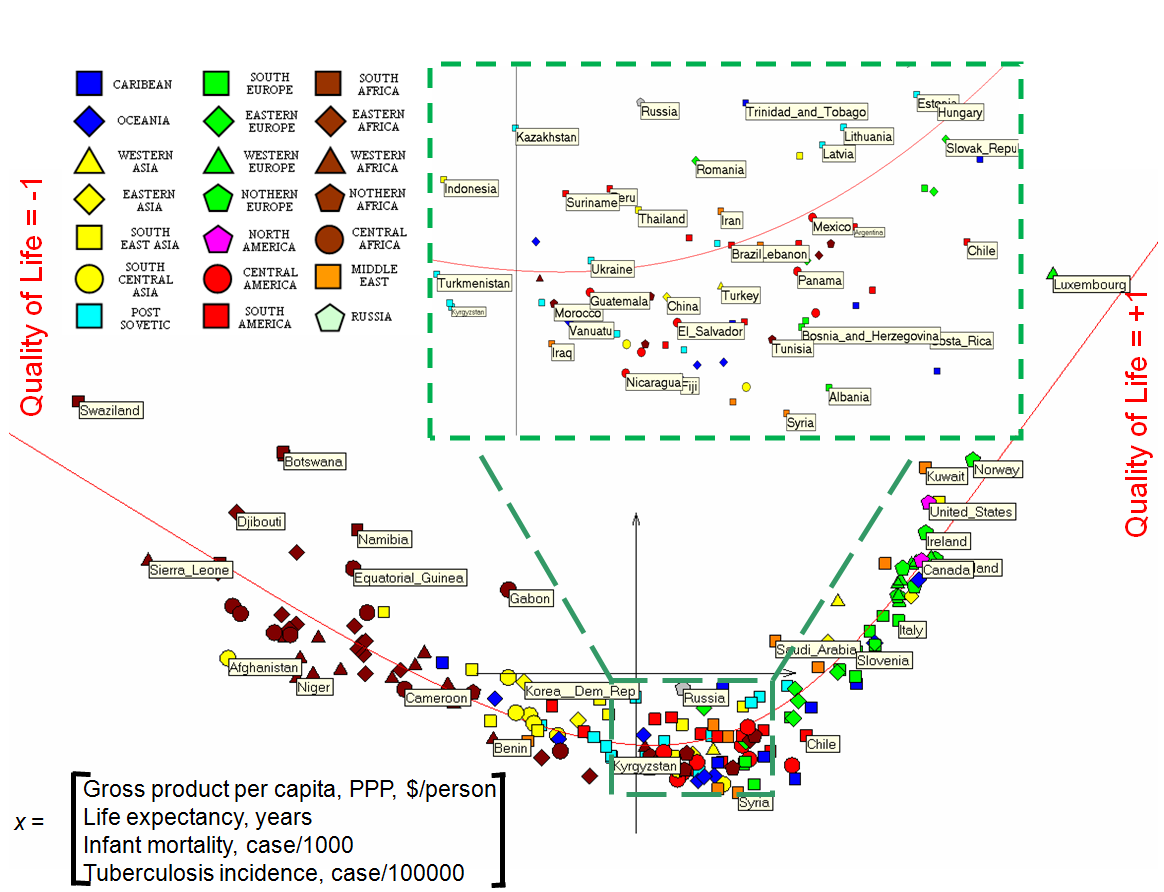
Applications

Most important applications of the method and free software are in bioinformatics for exploratory data analysis and visualisation of multidimensional data, for data visualisation in economics, social and political sciences, as an auxiliary tool for data mapping in geographic informational systems and for visualisation of data of various nature.

The method is applied in quantitative biology for reconstructing the curved surface of a tree leaf from a stack of light microscopy images. This reconstruction is used for quantifying the geodesic distances between trichomes and their patterning, which is a marker of the capability of a plant to resist to pathogenes.

Recently, the method is adapted as a support tool in the decision process underlying the selection, optimization, and management of financial portfolios.

The method of elastic maps has been systematically tested and compared with several machine learning methods on the applied problem of identification of the flow regime of a gas-liquid flow in a pipe. There are various regimes: Single phase water or air flow, Bubbly flow, Bubbly-slug flow, Slug flow, Slug-churn flow, Churn flow, Churn-annular flow, and Annular flow. The simplest and most common method used to identify the flow regime is visual observation. This approach is, however, subjective and unsuitable for relatively high gas and liquid flow rates. Therefore, the machine learning methods are proposed by many authors. The methods are applied to differential pressure data collected during a calibration process. The method of elastic maps provided a 2D map, where the area of each regime is represented. The comparison with some other machine learning methods is presented in Table 1 for various pipe diameters and pressure.

Here, ANN stands for the backpropagation artificial neural networks, SVM stands for the support vector machine, SOM for the self-organizing maps. The hybrid technology was developed for engineering applications. In this technology, elastic maps are used in combination with Principal Component Analysis (PCA), Independent Component Analysis (ICA) and backpropagation ANN.

The textbookM. Resta
Computational Intelligence Paradigms in Economic and Financial Decision Making
Series Intelligent Systems Reference Library, Volume 99, Springer International Publishing, Switzerland 2016. provides a systematic comparison of elastic maps and self-organizing maps (SOMs) in applications to economic and financial decision-making.

References

{{reflist

Data mining
Dimension reduction