duoantiprism on:
[Wikipedia]
[Google]
[Amazon]
In
 The regular skew polyhedron, , exists in 4-space as the n2 square faces of a ''n-n duoprism'', using all 2n2 edges and n2 vertices. The 2''n'' ''n''-gonal faces can be seen as removed. (skew polyhedra can be seen in the same way by a n-m duoprism, but these are not ''regular''.)
The regular skew polyhedron, , exists in 4-space as the n2 square faces of a ''n-n duoprism'', using all 2n2 edges and n2 vertices. The 2''n'' ''n''-gonal faces can be seen as removed. (skew polyhedra can be seen in the same way by a n-m duoprism, but these are not ''regular''.)
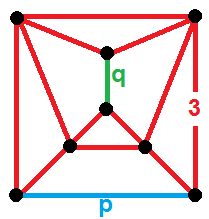 Like the
Like the
geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
of 4 dimensions or higher, a double prism or duoprism is a polytope
In elementary geometry, a polytope is a geometric object with flat sides ('' faces''). Polytopes are the generalization of three-dimensional polyhedra to any number of dimensions. Polytopes may exist in any general number of dimensions as an ...
resulting from the Cartesian product
In mathematics, specifically set theory, the Cartesian product of two sets and , denoted , is the set of all ordered pairs where is an element of and is an element of . In terms of set-builder notation, that is
A\times B = \.
A table c ...
of two polytopes, each of two dimensions or higher. The Cartesian product of an -polytope and an -polytope is an -polytope, where and are dimensions of 2 (polygon
In geometry, a polygon () is a plane figure made up of line segments connected to form a closed polygonal chain.
The segments of a closed polygonal chain are called its '' edges'' or ''sides''. The points where two edges meet are the polygon ...
) or higher.
The lowest-dimensional duoprisms exist in 4-dimensional space as 4-polytope
In geometry, a 4-polytope (sometimes also called a polychoron, polycell, or polyhedroid) is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: Vertex (geometry), vertices, Edge (geo ...
s being the Cartesian product of two polygons in 2-dimensional Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
. More precisely, it is the set
Set, The Set, SET or SETS may refer to:
Science, technology, and mathematics Mathematics
*Set (mathematics), a collection of elements
*Category of sets, the category whose objects and morphisms are sets and total functions, respectively
Electro ...
of points:
:
where and are the sets of the points contained in the respective polygons. Such a duoprism is convex
Convex or convexity may refer to:
Science and technology
* Convex lens, in optics
Mathematics
* Convex set, containing the whole line segment that joins points
** Convex polygon, a polygon which encloses a convex set of points
** Convex polytop ...
if both bases are convex, and is bounded by prismatic cells.
Nomenclature
Four-dimensional duoprisms are considered to be prismatic 4-polytopes. A duoprism constructed from tworegular polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either ''convex ...
s of the same edge length is a uniform duoprism.
A duoprism made of ''n''-polygons and ''m''-polygons is named by prefixing 'duoprism' with the names of the base polygons, for example: a ''triangular-pentagonal duoprism'' is the Cartesian product of a triangle and a pentagon.
An alternative, more concise way of specifying a particular duoprism is by prefixing with numbers denoting the base polygons, for example: 3,5-duoprism for the triangular-pentagonal duoprism.
Other alternative names:
* q-gonal-p-gonal prism
* q-gonal-p-gonal double prism
* q-gonal-p-gonal hyperprism
The term ''duoprism'' is coined by George Olshevsky, shortened from ''double prism''. John Horton Conway
John Horton Conway (26 December 1937 – 11 April 2020) was an English mathematician. He was active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory. He also made contributions to many b ...
proposed a similar name proprism
In geometry of 4 dimensions or higher, a proprism is a polytope resulting from the Cartesian product of two or more polytopes, each of two dimensions or higher. The term was coined by John Horton Conway for ''product prism''. The dimension of the s ...
for ''product prism'', a Cartesian product of two or more polytopes of dimension at least two. The duoprisms are proprisms formed from exactly two polytopes.
Example 16-16 duoprism
Geometry of 4-dimensional duoprisms
A 4-dimensionaluniform
A uniform is a variety of costume worn by members of an organization while usually participating in that organization's activity. Modern uniforms are most often worn by armed forces and paramilitary organizations such as police, emergency serv ...
duoprism is created by the product of a regular ''n''-sided polygon
In geometry, a polygon () is a plane figure made up of line segments connected to form a closed polygonal chain.
The segments of a closed polygonal chain are called its '' edges'' or ''sides''. The points where two edges meet are the polygon ...
and a regular ''m''-sided polygon with the same edge length. It is bounded by ''n'' ''m''-gonal prisms and ''m'' ''n''-gonal prisms. For example, the Cartesian product of a triangle and a hexagon is a duoprism bounded by 6 triangular prisms and 3 hexagonal prisms.
*When ''m'' and ''n'' are identical, the resulting duoprism is bounded by 2''n'' identical ''n''-gonal prisms. For example, the Cartesian product of two triangles is a duoprism bounded by 6 triangular prisms.
*When ''m'' and ''n'' are identically 4, the resulting duoprism is bounded by 8 square prisms (cubes
A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It i ...
), and is identical to the tesseract
In geometry, a tesseract or 4-cube is a four-dimensional hypercube, analogous to a two-dimensional square and a three-dimensional cube. Just as the perimeter of the square consists of four edges and the surface of the cube consists of six ...
.
The ''m''-gonal prisms are attached to each other via their ''m''-gonal faces, and form a closed loop. Similarly, the ''n''-gonal prisms are attached to each other via their ''n''-gonal faces, and form a second loop perpendicular to the first. These two loops are attached to each other via their square faces, and are mutually perpendicular.
As ''m'' and ''n'' approach infinity, the corresponding duoprisms approach the duocylinder
The duocylinder, also called the double cylinder or the bidisc, is a geometric object embedded in 4-dimensional Euclidean space, defined as the Cartesian product of two disks of respective radii ''r''1 and ''r''2:
:D = \left\
It is similar t ...
. As such, duoprisms are useful as non-quadric
In mathematics, a quadric or quadric surface is a generalization of conic sections (ellipses, parabolas, and hyperbolas). In three-dimensional space, quadrics include ellipsoids, paraboloids, and hyperboloids.
More generally, a quadric hype ...
approximations of the duocylinder.
Nets
Perspective projections
A cell-centered perspective projection makes a duoprism look like atorus
In geometry, a torus (: tori or toruses) is a surface of revolution generated by revolving a circle in three-dimensional space one full revolution about an axis that is coplanarity, coplanar with the circle. The main types of toruses inclu ...
, with two sets of orthogonal cells, p-gonal and q-gonal prisms.
The p-q duoprisms are identical to the q-p duoprisms, but look different in these projections because they are projected in the center of different cells.
Orthogonal projections
Vertex-centered orthogonal projections of p-p duoprisms project into nsymmetry for odd degrees, and for even degrees. There are n vertices projected into the center. For 4,4, it represents the A3 Coxeter plane of thetesseract
In geometry, a tesseract or 4-cube is a four-dimensional hypercube, analogous to a two-dimensional square and a three-dimensional cube. Just as the perimeter of the square consists of four edges and the surface of the cube consists of six ...
. The 5,5 projection is identical to the 3D rhombic triacontahedron
The rhombic triacontahedron, sometimes simply called the triacontahedron as it is the most common thirty-faced polyhedron, is a convex polyhedron with 30 rhombus, rhombic face (geometry), faces. It has 60 edge (geometry), edges and 32 vertex ...
.
Related polytopes
 The regular skew polyhedron, , exists in 4-space as the n2 square faces of a ''n-n duoprism'', using all 2n2 edges and n2 vertices. The 2''n'' ''n''-gonal faces can be seen as removed. (skew polyhedra can be seen in the same way by a n-m duoprism, but these are not ''regular''.)
The regular skew polyhedron, , exists in 4-space as the n2 square faces of a ''n-n duoprism'', using all 2n2 edges and n2 vertices. The 2''n'' ''n''-gonal faces can be seen as removed. (skew polyhedra can be seen in the same way by a n-m duoprism, but these are not ''regular''.)
Duoantiprism
 Like the
Like the antiprism
In geometry, an antiprism or is a polyhedron composed of two Parallel (geometry), parallel Euclidean group, direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway po ...
s as alternated prism
PRISM is a code name for a program under which the United States National Security Agency (NSA) collects internet communications from various U.S. internet companies. The program is also known by the SIGAD . PRISM collects stored internet ...
s, there is a set of 4-dimensional duoantiprisms: 4-polytopes
In geometry, a 4-polytope (sometimes also called a polychoron, polycell, or polyhedroid) is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: vertices, edges, faces (polygons), ...
that can be created by an alternation operation applied to a duoprism. The alternated vertices create nonregular tetrahedral cells, except for the special case, the ''4-4 duoprism'' (tesseract
In geometry, a tesseract or 4-cube is a four-dimensional hypercube, analogous to a two-dimensional square and a three-dimensional cube. Just as the perimeter of the square consists of four edges and the surface of the cube consists of six ...
) which creates the uniform (and regular) 16-cell
In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the ...
. The 16-cell is the only convex uniform duoantiprism.
The duoprisms , t0,1,2,3, can be alternated into , ht0,1,2,3, the "duoantiprisms", which cannot be made uniform in general. The only convex uniform solution is the trivial case of p=q=2, which is a lower symmetry construction of the tesseract
In geometry, a tesseract or 4-cube is a four-dimensional hypercube, analogous to a two-dimensional square and a three-dimensional cube. Just as the perimeter of the square consists of four edges and the surface of the cube consists of six ...
, t0,1,2,3, with its alternation as the 16-cell
In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the ...
, , ss.
The only nonconvex uniform solution is p=5, q=5/3, ht0,1,2,3, , constructed from 10 pentagonal antiprism
In geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of ten triangles fo ...
s, 10 pentagrammic crossed-antiprism
In geometry, the pentagrammic crossed-antiprism is one in an infinite set of nonconvex antiprisms formed by triangle sides and two regular star polygon caps, in this case two pentagrams.
It differs from the pentagrammic antiprism by having oppos ...
s, and 50 tetrahedra, known as the great duoantiprism (gudap).http://www.polychora.com/12GudapsMovie.gif Animation of cross sections
Ditetragoltriates
Also related are the ditetragoltriates or octagoltriates, formed by taking theoctagon
In geometry, an octagon () is an eight-sided polygon or 8-gon.
A '' regular octagon'' has Schläfli symbol and can also be constructed as a quasiregular truncated square, t, which alternates two types of edges. A truncated octagon, t is a ...
(considered to be a ditetragon or a truncated square) to a p-gon. The ''octagon'' of a p-gon can be clearly defined if one assumes that the octagon is the convex hull of two perpendicular rectangle
In Euclidean geometry, Euclidean plane geometry, a rectangle is a Rectilinear polygon, rectilinear convex polygon or a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that a ...
s; then the p-gonal ditetragoltriate is the convex hull of two p-p duoprisms (where the p-gons are similar but not congruent, having different sizes) in perpendicular orientations. The resulting polychoron is isogonal and has 2p p-gonal prisms and p2 rectangular trapezoprisms (a cube
A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It i ...
with ''D2d'' symmetry) but cannot be made uniform. The vertex figure is a triangular bipyramid
A triangular bipyramid is a hexahedron with six triangular faces constructed by attaching two tetrahedra face-to-face. The same shape is also known as a triangular dipyramid or trigonal bipyramid. If these tetrahedra are regular, all faces of a t ...
.
Double antiprismoids
Like the duoantiprisms as alternated duoprisms, there is a set of p-gonal double antiprismoids created by alternating the 2p-gonal ditetragoltriates, creating p-gonal antiprisms and tetrahedra while reinterpreting the non-corealmic triangular bipyramidal spaces as two tetrahedra. The resulting figure is generally not uniform except for two cases: thegrand antiprism
In geometry, the grand antiprism or pentagonal double antiprismoid is a uniform 4-polytope (4-dimensional uniform polytope) bounded by 320 cells: 20 pentagonal antiprisms, and 300 tetrahedra. It is an anomalous, non-Wythoffian uniform 4-polyto ...
and its conjugate, the pentagrammic double antiprismoid (with p = 5 and 5/3 respectively), represented as the alternation of a decagonal or decagrammic ditetragoltriate. The vertex figure is a variant of the sphenocorona.
k22 polytopes
The 3-3 duoprism, -122, is first in a dimensional series of uniform polytopes, expressed byCoxeter
Harold Scott MacDonald "Donald" Coxeter (9 February 1907 – 31 March 2003) was a British-Canadian geometer and mathematician. He is regarded as one of the greatest geometers of the 20th century.
Coxeter was born in England and educated ...
as k22 series. The 3-3 duoprism is the vertex figure for the second, the birectified 5-simplex. The fourth figure is a Euclidean honeycomb, 222, and the final is a paracompact hyperbolic honeycomb, 322, with Coxeter group 2,2,3 . Each progressive uniform polytope
In geometry, a uniform polytope of dimension three or higher is a vertex-transitive polytope bounded by uniform Facet (mathematics), facets. Here, "vertex-transitive" means that it has symmetries taking every vertex to every other vertex; the sam ...
is constructed from the previous as its vertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a general -polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connected ed ...
.
See also
*Polytope
In elementary geometry, a polytope is a geometric object with flat sides ('' faces''). Polytopes are the generalization of three-dimensional polyhedra to any number of dimensions. Polytopes may exist in any general number of dimensions as an ...
and 4-polytope
In geometry, a 4-polytope (sometimes also called a polychoron, polycell, or polyhedroid) is a four-dimensional polytope. It is a connected and closed figure, composed of lower-dimensional polytopal elements: Vertex (geometry), vertices, Edge (geo ...
*Convex regular 4-polytope
In mathematics, a regular 4-polytope or regular polychoron is a regular four-dimensional polytope. They are the four-dimensional analogues of the regular polyhedra in three dimensions and the regular polygons in two dimensions.
There are six co ...
*Duocylinder
The duocylinder, also called the double cylinder or the bidisc, is a geometric object embedded in 4-dimensional Euclidean space, defined as the Cartesian product of two disks of respective radii ''r''1 and ''r''2:
:D = \left\
It is similar t ...
*Tesseract
In geometry, a tesseract or 4-cube is a four-dimensional hypercube, analogous to a two-dimensional square and a three-dimensional cube. Just as the perimeter of the square consists of four edges and the surface of the cube consists of six ...
Notes
References
*''Regular Polytopes'', H. S. M. Coxeter, Dover Publications, Inc., 1973, New York, p. 124. *Coxeter
Harold Scott MacDonald "Donald" Coxeter (9 February 1907 – 31 March 2003) was a British-Canadian geometer and mathematician. He is regarded as one of the greatest geometers of the 20th century.
Coxeter was born in England and educated ...
, ''The Beauty of Geometry: Twelve Essays'', Dover Publications, 1999, (Chapter 5: Regular Skew Polyhedra in three and four dimensions and their topological analogues)
** Coxeter, H. S. M. ''Regular Skew Polyhedra in Three and Four Dimensions.'' Proc. London Math. Soc. 43, 33-62, 1937.
* John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ''The Symmetries of Things'' 2008, {{ISBN, 978-1-56881-220-5 (Chapter 26)
* N.W. Johnson: ''The Theory of Uniform Polytopes and Honeycombs'', Ph.D. Dissertation, University of Toronto, 1966
Uniform 4-polytopes