Drainage equation on:
[Wikipedia]
[Google]
[Amazon]
A drainage equation is an equation describing the relation between depth and spacing of parallel subsurface drains, depth of the watertable, depth and  A well known
A well known
In
For the derivation of the equation Hooghoudt used the law of Darcy, the summation of circular potential functions and, for the determination of the influence of the impermeable layer, de method of
Hooghoudt published tables for the determination of the equivalent depth (d), because the function (F) in d = F (L,Di-Dd,r) consists of long series of terms. ''Determining:''
*the discharge rate (Q) from the recharge rate (R) in a
''Determining:''
*the discharge rate (Q) from the recharge rate (R) in a
One would not want the water table to be too shallow to avoid crop yield depression nor too deep to avoid drought conditions. This is a subject of drainage research. The figure shows that a seasonal average depth of the water table shallower than 70 cm causes a yield depression
The figure was made with the SegReg program for segmented regression.
Image:SlopingLandDrains.jpg, Geometry of drains in sloping land used in the theory
Image:SandTankDrains.jpg, Corroboration with drainage experiments in a sloping sand tank
Image:Entrance resistance.jpg, Definition of entrance resistance
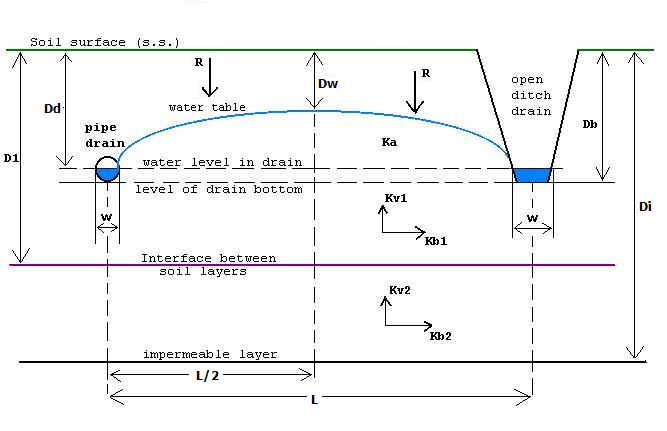
 The drainage formula can be amplified to account for (see figure on the right):
*the additional energy associated with the incoming percolation water ( recharge), see groundwater energy balance
*multiple soil layers
*
The drainage formula can be amplified to account for (see figure on the right):
*the additional energy associated with the incoming percolation water ( recharge), see groundwater energy balance
*multiple soil layers
*
or from
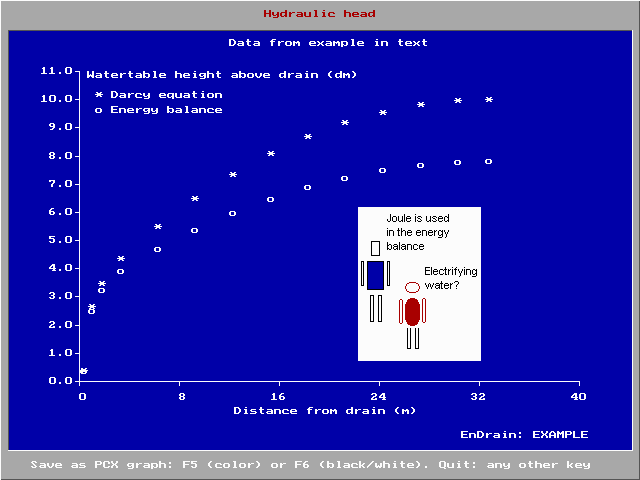
/ref> It shows that incorporation of the incoming energy associated with the recharge leads to a somewhat deeper watertable, water table.
Drainage Hooghoudt's equation calculator
{{DEFAULTSORT:Drainage Equation Drainage Hydrology Hydraulic engineering Soil Soil science Soil physics Agricultural soil science
hydraulic conductivity
In science and engineering, hydraulic conductivity (, in SI units of meters per second), is a property of porous materials, soils and Rock (geology), rocks, that describes the ease with which a fluid (usually water) can move through the porosity, ...
of the soils. It is used in drainage
Drainage is the natural or artificial removal of a surface's water and sub-surface water from an area with excess water. The internal drainage of most agricultural soils can prevent severe waterlogging (anaerobic conditions that harm root gro ...
design.
steady-state
In systems theory, a system or a process is in a steady state if the variables (called state variables) which define the behavior of the system or the process are unchanging in time. In continuous time, this means that for those properties ''p'' ...
drainage equation is the Hooghoudt drain spacing equation. Its original publication is in Dutch. The equation was introduced in the USA by van Schilfgaarde.
Hooghoudt's equation
Hooghoudt's equation can be written as:. :Q L2 = 8 Kb d (Dd - Dw) + 4 Ka (Dd - Dw)2 where: * Q =steady state
In systems theory, a system or a process is in a steady state if the variables (called state variables) which define the behavior of the system or the process are unchanging in time. In continuous time, this means that for those properties ''p' ...
drainage discharge rate (m/day)
* Ka = hydraulic conductivity
In science and engineering, hydraulic conductivity (, in SI units of meters per second), is a property of porous materials, soils and Rock (geology), rocks, that describes the ease with which a fluid (usually water) can move through the porosity, ...
of the soil above drain level (m/day)
* Kb = hydraulic conductivity
In science and engineering, hydraulic conductivity (, in SI units of meters per second), is a property of porous materials, soils and Rock (geology), rocks, that describes the ease with which a fluid (usually water) can move through the porosity, ...
of the soil below drain level (m/day)
* Di = depth of the impermeable layer below drain level (m)
* Dd = depth of the drains (m)
* Dw = steady state depth of the watertable midway between the drains (m)
* L = spacing between the drains (m)
* d = equivalent depth, a function of L, (Di-Dd), and r
* r = drain radius (m)
''Steady (equilibrium) state condition'' In
steady state
In systems theory, a system or a process is in a steady state if the variables (called state variables) which define the behavior of the system or the process are unchanging in time. In continuous time, this means that for those properties ''p' ...
, the level of the water table remains constant and the discharge rate (Q) equals the rate of groundwater recharge
Groundwater recharge or deep drainage or deep percolation is a hydrologic process, where water moves downward from surface water to groundwater. Recharge is the primary method through which water enters an aquifer. This process usually occurs in ...
(R), i.e. the amount of water entering the groundwater
Groundwater is the water present beneath Earth's surface in rock and Pore space in soil, soil pore spaces and in the fractures of stratum, rock formations. About 30 percent of all readily available fresh water in the world is groundwater. A unit ...
through the watertable per unit of time. By considering a long-term (e.g. seasonal) average depth of the water table (Dw) in combination with the long-term average recharge rate (R), the net storage of water in that period of time is negligibly small and the steady state condition is satisfied: one obtains a dynamic equilibrium
In chemistry, a dynamic equilibrium exists once a reversible reaction occurs. Substances initially transition between the reactants and products at different rates until the forward and backward reaction rates eventually equalize, meaning the ...
.
''Derivation of the equation'' For the derivation of the equation Hooghoudt used the law of Darcy, the summation of circular potential functions and, for the determination of the influence of the impermeable layer, de method of
mirror image
A mirror image (in a plane mirror) is a reflection (physics), reflected duplication of an object that appears almost identical, but is reversed in the direction perpendicular to the mirror surface. As an optical phenomenon, optical effect, it r ...
s and superposition. Hooghoudt published tables for the determination of the equivalent depth (d), because the function (F) in d = F (L,Di-Dd,r) consists of long series of terms.
water balance
The law of water balance states that the inflows to any water system or area is equal to its outflows plus change in storage during a time interval. In hydrology, a water balance equation can be used to describe the flow of water in and out of ...
as detailed in the article: hydrology (agriculture)
Agricultural hydrology is the study of water balance components intervening in farm water, agricultural water management, especially in irrigation and drainage.
Water balance components
The water balance components can be grouped into componen ...
*the permissible long term average depth of the water table (Dw) on the basis of ''agricultural drainage criteria''
*the soil's hydraulic conductivity
In science and engineering, hydraulic conductivity (, in SI units of meters per second), is a property of porous materials, soils and Rock (geology), rocks, that describes the ease with which a fluid (usually water) can move through the porosity, ...
(Ka and Kb) by measurements
*the depth of the bottom of the aquifer
An aquifer is an underground layer of water-bearing material, consisting of permeability (Earth sciences), permeable or fractured rock, or of unconsolidated materials (gravel, sand, or silt). Aquifers vary greatly in their characteristics. The s ...
(Di)
the design drain spacing (L) can be found from the equation in dependence of the drain depth (Dd) and drain radius (r).
''Drainage criteria'' One would not want the water table to be too shallow to avoid crop yield depression nor too deep to avoid drought conditions. This is a subject of drainage research. The figure shows that a seasonal average depth of the water table shallower than 70 cm causes a yield depression
The figure was made with the SegReg program for segmented regression.
Equivalent depth
In 1991 aclosed-form expression
In mathematics, an expression or equation is in closed form if it is formed with constants, variables, and a set of functions considered as ''basic'' and connected by arithmetic operations (, and integer powers) and function composition. ...
was developed for the equivalent depth (d) that can replace the Hooghoudt tables:
:d = πL / 8
where:
*x = 2π (Di − Dd) / L
*F(x) = Σ 4e−2nx / n (1 − e−2nx), with n = 1, 3, 5, . . .
Extended use
Theoretically, Hooghoudt's equation can also be used for ''sloping land''. The theory on drainage of sloping land is corroborated by the results of sand tank experiments. In addition, the ''entrance resistance'' encountered by the water upon entering the drains can be accounted for.Amplification
 The drainage formula can be amplified to account for (see figure on the right):
*the additional energy associated with the incoming percolation water ( recharge), see groundwater energy balance
*multiple soil layers
*
The drainage formula can be amplified to account for (see figure on the right):
*the additional energy associated with the incoming percolation water ( recharge), see groundwater energy balance
*multiple soil layers
*anisotropic
Anisotropy () is the structural property of non-uniformity in different directions, as opposed to isotropy. An anisotropic object or pattern has properties that differ according to direction of measurement. For example, many materials exhibit ver ...
hydraulic conductivity, the vertical conductivity (Kv) being different from the horizontal (Kh)
*drains of different dimensions with any width (W)
Computer program
The amplified drainage equation uses an hydraulic equivalent of Joule's law in electricity. It is in the form of a differential equation that cannot be solved analytically (i.e. in a closed form) but the solution requires anumerical method
In numerical analysis, a numerical method is a mathematical tool designed to solve numerical problems. The implementation of a numerical method with an appropriate convergence check in a programming language is called a numerical algorithm.
Mathem ...
for which a computer program
A computer program is a sequence or set of instructions in a programming language for a computer to Execution (computing), execute. It is one component of software, which also includes software documentation, documentation and other intangibl ...
is indispensable.
The availability of a computer program also helps in quickly assessing various alternatives and performing a sensitivity analysis
Sensitivity analysis is the study of how the uncertainty in the output of a mathematical model or system (numerical or otherwise) can be divided and allocated to different sources of uncertainty in its inputs. This involves estimating sensitivity ...
.
The blue figure shows an example of results of a computer aided calculation with the amplified drainage equation using the EnDrain program.The free computer program EnDrain can be downloaded from web page or from
/ref> It shows that incorporation of the incoming energy associated with the recharge leads to a somewhat deeper watertable, water table.
References
External links
Drainage Hooghoudt's equation calculator
{{DEFAULTSORT:Drainage Equation Drainage Hydrology Hydraulic engineering Soil Soil science Soil physics Agricultural soil science