Dixon elliptic functions

In mathematics, the Dixon elliptic functions sm and cm are two elliptic functions (doubly periodic meromorphic functions on the complex plane) that map from each regular hexagon in a hexagonal tiling to the whole complex plane. Because these functions satisfy the identity $\operatorname^3 z + \operatorname^3 z = 1$, as real functions they parametrize the cubic Fermat curve $x^3 + y^3 = 1$, just as the trigonometric functions sine and cosine parametrize the unit circle $x^2 + y^2 = 1$.

They were named sm and cm by Alfred Dixon in 1890, by analogy to the trigonometric functions sine and cosine and the Jacobi elliptic functions sn and cn; Göran Dillner described them earlier in 1873.

Definition

The functions sm and cm can be defined as the solutions to the initial value problem:

:$\frac \operatorname z = -\operatorname^2 z,\ \frac \operatorname z = \operatorname^2 z,\ \operatorname(0) = 1,\ \operatorname(0) = 0$

Or as the inverse of the Schwarz–Christoffel mapping from the complex unit disk to an equilateral triangle, the Abelian integral:

:$z = \int_0^ \frac = \int_^1 \frac$

which can also be expressed using the hypergeometric function:
:$\operatorname^(z) = z\; _2F_1\bigl(\tfrac13, \tfrac23; \tfrac43; z^3\bigr)$

Parametrization of the cubic Fermat curve

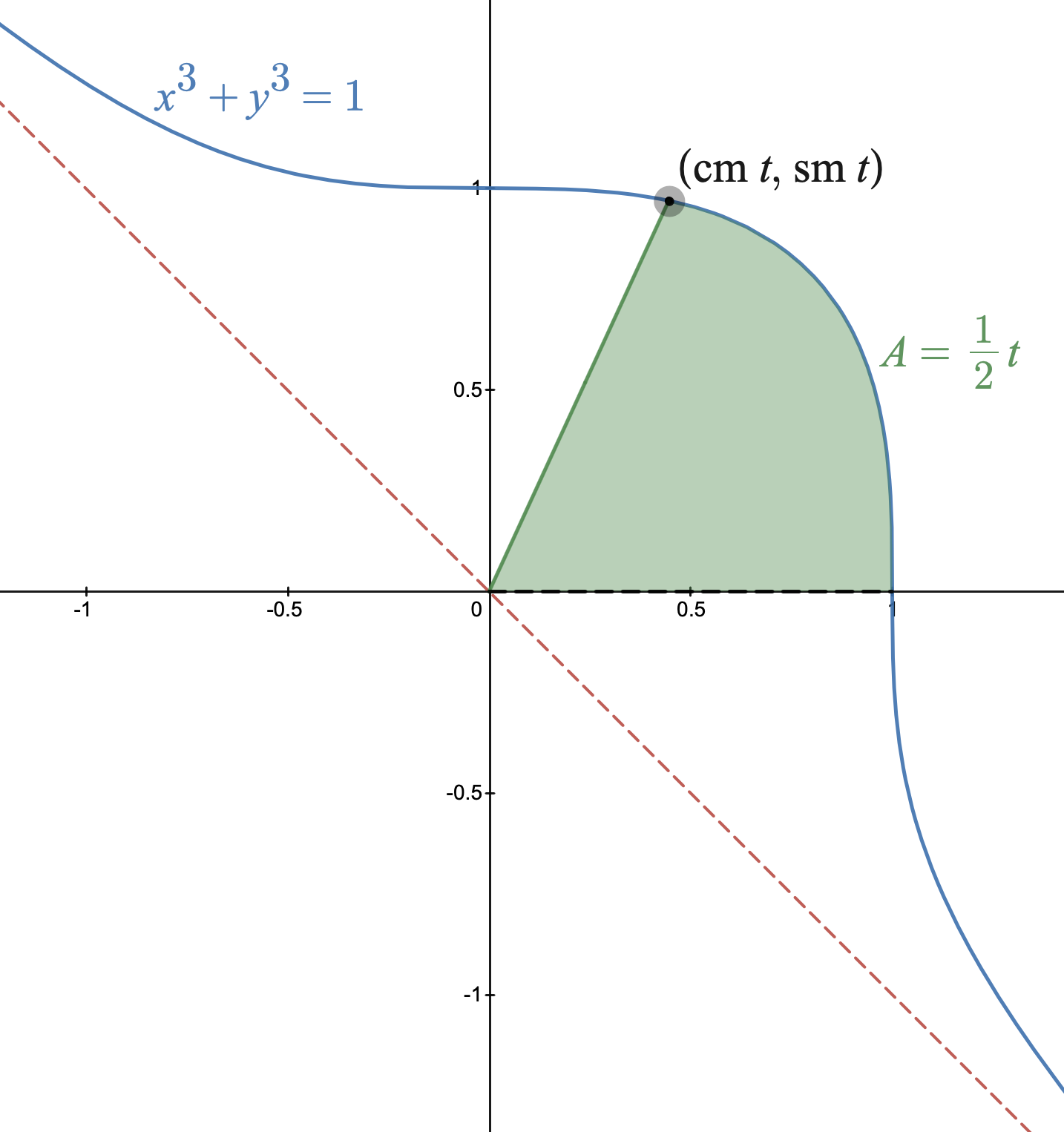
Both sm and cm have a period along the real axis of $\pi_3 = \Beta\bigl( \tfrac13, \tfrac13\bigr) = \tfrac\Gamma^3\bigl(\tfrac\bigr)\approx 5.29991625$ with $\Beta$ the beta function and $\Gamma$ the gamma function:

:\begin \tfrac13\pi_3 &= \int_^0 \frac = \int_0^1 \frac = \int_1^\infty \frac \\ mu&\approx 1.76663875 \end

They satisfy the identity $\operatorname^3 z + \operatorname^3 z = 1$. The parametric function $t \mapsto (\operatorname t,\, \operatorname t),$ t \in \bigl pi_3, \tfrac23\pi_3\bigr/math> parametrizes the cubic Fermat curve $x^3 + y^3 = 1,$ with $\tfrac12 t$ representing the signed area lying between the segment from the origin to $(1,\, 0)$, the segment from the origin to $(\operatorname t,\, \operatorname t)$, and the Fermat curve, analogous to the relationship between the argument of the trigonometric functions and the area of a sector of the unit circle. To see why, apply Green's theorem:

:$A = \tfrac 12 \int_0^t (x\mathop -y\mathop) = \tfrac 12 \int_0^t (\operatorname^3 t + \operatorname^3 t)\mathop = \tfrac 12 \int_0^t dt = \tfrac12 t.$

Notice that the area between the $x + y = 0$ and $x^3 + y^3 = 1$ can be broken into three pieces, each of area $\tfrac16\pi_3$:

:\begin
\tfrac12\pi_3 &= \int_^\infty \bigl((1 - x^3)^ + x\bigr)\mathop \\ mu\tfrac16\pi_3 &= \int_^0 \bigl((1 - x^3)^ + x\bigr)\mathop = \int_0^1 (1 - x^3)^ \mathop.
\end

Symmetries

The function $\operatorname z$ has zeros at the complex-valued points $z = \tfrac1\sqrt\pi_3i(a + b\omega)$ for any integers $a$ and $b$, where $\omega$ is a cube root of unity, $\omega = \exp \tfrac23 i \pi = -\tfrac12 + \tfrac\sqrt2i$ (that is, $a + b\omega$ is an Eisenstein integer). The function $\operatorname z$ has zeros at the complex-valued points $z = \tfrac13\pi_3 + \tfrac1\sqrt\pi_3i(a + b\omega)$. Both functions have poles at the complex-valued points $z = -\tfrac13\pi_3 + \tfrac1\sqrt\pi_3i(a + b\omega)$.

On the real line, $\operatornamex=0\leftrightarrow x\in\pi_3\mathbb$, which is analogous to $\sin x=0\leftrightarrow x\in\pi\mathbb$.

Fundamental reflections, rotations, and translations

: $\operatorname \bar = \overline$
: $\operatorname \bar = \overline$
: $\operatorname( - z ) = \frac = \operatorname \bigl(z + \tfrac13\pi_3\bigr)$
: $\operatorname( - z ) = -\frac = \frac = \operatorname \bigl(z + \tfrac13\pi_3\bigr)$
: $\operatorname \omega z = \operatorname z = \operatorname \omega^2 z$
: $\operatorname \omega z = \omega \operatorname z = \omega^2 \operatorname \omega^2 z$
: $\operatorname\bigl( z + \pi_3(a + b\omega) \bigr) = \operatorname z$
: $\operatorname\bigl( z + \pi_3(a + b\omega) \bigr) = \operatorname z,$ where $a + b\omega$ is any Eisenstein integer.

Specific values

Identities

Sum and difference

The Dixon elliptic functions satisfy the argument sum and difference identities:

\begin
\operatorname( u + v ) &= \frac

\\ mu\operatorname( u - v ) &= \frac

\\ mu\operatorname( u + v ) &= \frac

\\ mu\operatorname( u - v ) &= \frac

\end

Multiplication

Duplication identities can't be derived fron sum identity beause it will result $0/0$, so they instead should be derived from difference and reflexion identities.

\begin
\operatorname( 2u ) &= \frac

\\ mu\operatorname( 2u ) &= \frac

\\ mu\operatorname( 3u ) &= \frac

\\ mu\operatorname( 3u ) &= \frac

\\ mu\operatorname( nu ) &= \frac

\\ mu\operatorname( nu ) &= \frac

\end

Other expressions

Power series expansion

The coefficients $c_n$ and $s_n$ of the power series expansions

:\begin
\operatorname z &= c_0 + c_1z^3 + c_2z^6 + c_3z^ + \cdots + c_nz^ + \cdots \\ mu\operatorname z &= s_0z + s_1z^4 + s_2z^7 + s_3z^ + \cdots + s_nz^ + \cdots
\end

satisfy the recurrence $c_0 = s_0 = 1,$

:\begin
c_n &= -\frac\sum_^ s_ks_ \\ mus_n &= \frac\sum_^n c_kc_
\end

These recurrences result in:

:\begin
\operatorname z &= 1 - \fracz^3 + \fracz^6 - \fracz^ + \fracz^ - \fracz^ + \cdots \\ mu\operatorname z &= z -\fracz^4 + \fracz^7 - \fracz^ + \fracz^ - \fracz^ + \cdots
\end

Weierstrass elliptic function

The equianharmonic Weierstrass elliptic function $\wp(z) = \wp\bigl(z; 0, \tfrac1\bigr),$ with lattice $\Lambda = \pi_3\mathbb \oplus \pi_3\omega\mathbb$ a scaling of the Eisenstein integers, can be defined as:

:$\wp(z) = \frac + \sum_\!\left(\frac 1 - \frac 1 \right)$

The function $\wp(z)$ solves the differential equation:

:$\wp'(z)^2 = 4\wp(z)^3 - \tfrac1$

We can also write it as the inverse of the integral:

:$z = \int_^ \frac$

In terms of $\wp(z)$, the Dixon elliptic functions can be written:

: $\operatorname z = \frac,\ \operatorname z = \frac$

Likewise, the Weierstrass elliptic function $\wp(z) = \wp\bigl(z; 0, \tfrac1\bigr)$ can be written in terms of Dixon elliptic functions:

: $\wp'(z) = \frac,\ \wp(z) = \frac$

Jacobi elliptic functions

The Dixon elliptic functions can also be expressed using Jacobi elliptic functions, which was first observed by Cayley. Let $k = e^$, $\theta = 3^ e^$, $s = \operatorname (u,k)$, $c = \operatorname (u,k)$, and $d = \operatorname (u,k)$. Then, let

: $\xi(u) = \frac$, $\eta(u) = \frac$.

Finally, the Dixon elliptic functions are as so:

: $\operatorname (z) = \xi \left(\frac\right)$, $\operatorname (z) = \eta \left(\frac\right)$.

Generalized trigonometry

Several definitions of generalized trigonometric functions include the usual trigonometric sine and cosine as an $n = 2$ case, and the functions sm and cm as an $n = 3$ case.

For example, defining $\pi_n = \Beta\bigl(\tfrac1n, \tfrac1n\bigr)$ and $\sin_n z,\,\cos_n z$ the inverses of an integral:

:$z = \int_0^ \frac = \int_^1 \frac$

The area in the positive quadrant under the curve $x^n + y^n = 1$ is

:$\int_0^ (1 - x^n)^\mathop = \frac$.

Applications

The Dixon elliptic functions are conformal maps from an equilateral triangle to a disk, and are therefore helpful for constructing polyhedral conformal map projections involving equilateral triangles, for example projecting the sphere onto a triangle, hexagon, tetrahedron, octahedron, or icosahedron.Adams (1925), Cox (1935), Magis (1938), Lee (1973), Lee (1976), McIlroy (2011), Chapling (2016).

See also

* Eisenstein integer
* Elliptic function
** Abel elliptic functions
** Jacobi elliptic functions
** Lemniscate elliptic functions
** Weierstrass elliptic function
* Lee conformal world in a tetrahedron
* Schwarz–Christoffel mapping

External links

* Desmos plots:
** Real-valued Dixon elliptic functions https://www.desmos.com/calculator/5s4gdcnxh2.
** Parametrizing the cubic Fermat curve, https://www.desmos.com/calculator/elqqf4nwas
* On-Line Encyclopedia of Integer Sequences pages:
** “Coefficient of x^(3n+1)/(3n+1)! in the Maclaurin expansion of the Dixon elliptic function sm(x,0).” https://oeis.org/A104133
** “Coefficient of x^(3n)/(3n)! in the Maclaurin expansion of the Dixon elliptic function cm(x,0).” https://oeis.org/A104134
** “Pi(3): fundamental real period of the Dixonian elliptic functions sm(z) and cm(z).” https://oeis.org/A197374
* Mathematics Stack Exchange discussions:
** “On $x^3+y^3=z^3$, the Dixonian elliptic functions, and the Borwein cubic theta functions”, https://math.stackexchange.com/questions/2090523/
** “doubly periodic functions as tessellations (other than parallelograms)”, https://math.stackexchange.com/questions/35671/

Notes

References

* O. S. Adams (1925). ''Elliptic functions applied to conformal world maps'' (No. 297). US Government Printing Office. ftp://ftp.library.noaa.gov/docs.lib/htdocs/rescue/cgs_specpubs/QB275U35no1121925.pdf
* R. Bacher & P. Flajolet (2010) “Pseudo-factorials, elliptic functions, and continued fractions” ''The Ramanujan journal'' 21(1), 71–97. https://arxiv.org/pdf/0901.1379.pdf
* A. Cayley (1882) “Reduction of $\int dx / (1 - x^3)^$ to elliptic integrals”. ''Messenger of Mathematics'' 11, 142–143. https://gdz.sub.uni-goettingen.de/id/PPN599484047_0011?tify=
* F. D. Burgoyne (1964) “Generalized trigonometric functions”. ''Mathematics of Computation'' 18(86), 314–316. https://www.jstor.org/stable/2003310
* A. Cayley (1883) “On the elliptic function solution of the equation ”, ''Proceedings of the Cambridge Philosophical Society'' 4, 106–109. https://archive.org/details/proceedingsofcam4188083camb/page/106/
* R. Chapling (2016) “Invariant Meromorphic Functions on the Wallpaper Groups”. https://arxiv.org/pdf/1608.05677
* J. F. Cox (1935) “Répresentation de la surface entière de la terre dans une triangle équilatéral”, ''Bulletin de la Classe des Sciences, Académie Royale de Belgique 5e'', 21, 66–71.
* G. Dillner (1873) “Traité de calcul géométrique supérieur”, Chapter 16, ''Nova acta Regiae Societatis Scientiarum Upsaliensis, Ser. III'' 8, 94–102. https://archive.org/details/novaactaregiaeso38kung/page/94/
*
* A. Dixon (1894) ''The elementary properties of the elliptic functions''. MacMillian. https://archive.org/details/elempropellipt00dixorich/
*
* A. Gambini, G. Nicoletti, & D. Ritelli (2021) “Keplerian trigonometry”. ''Monatshefte für Mathematik'' 195(1), 55–72. https://doi.org/10.1007/s00605-021-01512-0
* R. Grammel (1948) “Eine Verallgemeinerung der Kreis-und Hyperbelfunktionen”. ''Archiv der Mathematik'' 1(1), 47–51. https://doi.org/10.1007/BF02038206
* J. C. Langer & D. A. Singer (2014) “The Trefoil”. ''Milan Journal of Mathematics'' 82(1), 161-182. https://case.edu/artsci/math/langer/jlpreprints/Trefoil.pdf
* M. Laurent (1949) “Tables de la fonction elliptique de Dixon pour l’intervalle 0-0, 1030”. ''Bulletin de l’Académie Royale des Sciences de Belgique Classe des Sciences'', 35, 439–450.
* L. P. Lee (1973) “The Conformal Tetrahedric Projection with some Practical Applications”. ''The Cartographic Journal'', 10(1), 22-28. https://doi.org/10.1179/caj.1973.10.1.22
* L. P. Lee (1976)
Conformal Projections Based on Elliptic Functions
'. University of Toronto Press. ''Cartographica'' Monograph No. 16.
* E. Lundberg (1879) “Om hypergoniometriska funktioner af komplexa variabla”. Manuscript, 1879. Translation by Jaak Peetre “On hypergoniometric functions of complex variables”. https://web.archive.org/web/20161024183030/http://www.maths.lth.se/matematiklu/personal/jaak/hypergf.ps
* J. Magis (1938) “Calcul du canevas de la représentation conforme de la sphère entière dans un triangle équilatéral”. ''Bulletin Géodésique'' 59(1), 247–256. http://doi.org/10.1007/BF03029866
* M. D. McIlroy (2011) “Wallpaper maps”. ''Dependable and Historic Computing''. Springer. 358–375. https://link.springer.com/chapter/10.1007/978-3-642-24541-1_27
* W. P. Reinhardt & P. L. Walker (2010) “Weierstrass Elliptic and Modular Functions”, ''NIST Digital Library of Mathematical Functions'', §23.5(v). https://dlmf.nist.gov/23.5#v
* P. L. Robinson (2019) “The Dixonian elliptic functions”. https://arxiv.org/abs/1901.04296
* H. A. Schwarz (1869) “Ueber einige Abbildungsaufgaben”. ''Crelles Journal'' 1869(70), 105–120. http://doi.org/10.1515/crll.1869.70.105
* B. R. Seth & F. P. White (1934) “Torsion of beams whose cross-section is a regular polygon of n sides”. ''Mathematical Proceedings of the Cambridge Philosophical Society'', 30(2), 139. http://doi.org/10.1017/s0305004100016558 
* D. Shelupsky (1959) “A generalization of the trigonometric functions”. ''The American Mathematical Monthly'' 66(10), 879–884. https://www.jstor.org/stable/2309789
{{refend

Complex analysis