Distance Sampling on:
[Wikipedia]
[Google]
[Amazon]
Distance sampling is a widely used group of closely related methods for estimating the
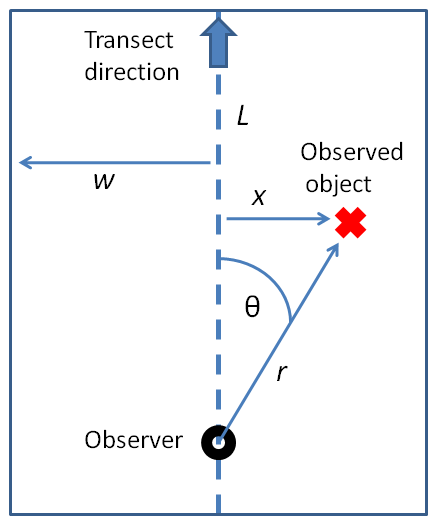 A common approach to distance sampling is the use of line transects. The observer traverses a straight line (placed randomly or following some planned distribution). Whenever they observe an object of interest (e.g., an animal of the type being surveyed), they record the distance from their current position to the object (''r''), as well as the angle of the detection to the transect line (''θ''). The distance of the object to the transect can then be calculated as ''x'' = ''r'' * sin(''θ''). These distances ''x'' are the detection distances that will be analyzed in further modeling.
Objects are detected out to a pre-determined maximum detection distance ''w''. Not all objects within ''w'' will be detected, but a fundamental assumption is that all objects at zero distance (i.e., on the line itself) are detected. Overall detection probability is thus expected to be 1 on the line, and to decrease with increasing distance from the line. The distribution of the observed distances is used to estimate a "detection function" that describes the probability of detecting an object at a given distance. Given that various basic assumptions hold, this function allows the estimation of the average probability ''P'' of detecting an object given that is within width ''w'' of the line. Object density can then be estimated as , where ''n'' is the number of objects detected and ''a'' is the size of the region covered (total length of the transect (''L'') multiplied by 2''w'').
In summary, modeling how detectability drops off with increasing distance from the transect allows estimating how many objects there are in total in the area of interest, based on the number that were actually observed.
The survey methodology for point transects is slightly different. In this case, the observer remains stationary, the survey ends not when the end of the transect is reached but after a pre-determined time, and measured distances to the observer are used directly without conversion to transverse distances. Detection function types and fitting are also different to some degree.
A common approach to distance sampling is the use of line transects. The observer traverses a straight line (placed randomly or following some planned distribution). Whenever they observe an object of interest (e.g., an animal of the type being surveyed), they record the distance from their current position to the object (''r''), as well as the angle of the detection to the transect line (''θ''). The distance of the object to the transect can then be calculated as ''x'' = ''r'' * sin(''θ''). These distances ''x'' are the detection distances that will be analyzed in further modeling.
Objects are detected out to a pre-determined maximum detection distance ''w''. Not all objects within ''w'' will be detected, but a fundamental assumption is that all objects at zero distance (i.e., on the line itself) are detected. Overall detection probability is thus expected to be 1 on the line, and to decrease with increasing distance from the line. The distribution of the observed distances is used to estimate a "detection function" that describes the probability of detecting an object at a given distance. Given that various basic assumptions hold, this function allows the estimation of the average probability ''P'' of detecting an object given that is within width ''w'' of the line. Object density can then be estimated as , where ''n'' is the number of objects detected and ''a'' is the size of the region covered (total length of the transect (''L'') multiplied by 2''w'').
In summary, modeling how detectability drops off with increasing distance from the transect allows estimating how many objects there are in total in the area of interest, based on the number that were actually observed.
The survey methodology for point transects is slightly different. In this case, the observer remains stationary, the survey ends not when the end of the transect is reached but after a pre-determined time, and measured distances to the observer are used directly without conversion to transverse distances. Detection function types and fitting are also different to some degree.
 The drop-off of detectability with increasing distance from the transect line is modeled using a detection function g(''y'') (here ''y'' is distance from the line). This function is fitted to the distribution of detection ranges represented as a
The drop-off of detectability with increasing distance from the transect line is modeled using a detection function g(''y'') (here ''y'' is distance from the line). This function is fitted to the distribution of detection ranges represented as a
Bibliography of > 1400 scientific publications using the method
Environmental statistics Demography Sampling techniques
density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...
and/or abundance of population
Population is a set of humans or other organisms in a given region or area. Governments conduct a census to quantify the resident population size within a given jurisdiction. The term is also applied to non-human animals, microorganisms, and pl ...
s. The main methods are based on line transects or point transects.Buckland, S. T., Anderson, D. R., Burnham, K. P. and Laake, J. L. (1993). ''Distance Sampling: Estimating Abundance of Biological Populations''. London: Chapman and Hall. In this method of sampling, the data collected are the distances of the objects being surveyed from these randomly placed lines or points, and the objective is to estimate the average density of the objects within a region.
Basic line transect methodology
 A common approach to distance sampling is the use of line transects. The observer traverses a straight line (placed randomly or following some planned distribution). Whenever they observe an object of interest (e.g., an animal of the type being surveyed), they record the distance from their current position to the object (''r''), as well as the angle of the detection to the transect line (''θ''). The distance of the object to the transect can then be calculated as ''x'' = ''r'' * sin(''θ''). These distances ''x'' are the detection distances that will be analyzed in further modeling.
Objects are detected out to a pre-determined maximum detection distance ''w''. Not all objects within ''w'' will be detected, but a fundamental assumption is that all objects at zero distance (i.e., on the line itself) are detected. Overall detection probability is thus expected to be 1 on the line, and to decrease with increasing distance from the line. The distribution of the observed distances is used to estimate a "detection function" that describes the probability of detecting an object at a given distance. Given that various basic assumptions hold, this function allows the estimation of the average probability ''P'' of detecting an object given that is within width ''w'' of the line. Object density can then be estimated as , where ''n'' is the number of objects detected and ''a'' is the size of the region covered (total length of the transect (''L'') multiplied by 2''w'').
In summary, modeling how detectability drops off with increasing distance from the transect allows estimating how many objects there are in total in the area of interest, based on the number that were actually observed.
The survey methodology for point transects is slightly different. In this case, the observer remains stationary, the survey ends not when the end of the transect is reached but after a pre-determined time, and measured distances to the observer are used directly without conversion to transverse distances. Detection function types and fitting are also different to some degree.
A common approach to distance sampling is the use of line transects. The observer traverses a straight line (placed randomly or following some planned distribution). Whenever they observe an object of interest (e.g., an animal of the type being surveyed), they record the distance from their current position to the object (''r''), as well as the angle of the detection to the transect line (''θ''). The distance of the object to the transect can then be calculated as ''x'' = ''r'' * sin(''θ''). These distances ''x'' are the detection distances that will be analyzed in further modeling.
Objects are detected out to a pre-determined maximum detection distance ''w''. Not all objects within ''w'' will be detected, but a fundamental assumption is that all objects at zero distance (i.e., on the line itself) are detected. Overall detection probability is thus expected to be 1 on the line, and to decrease with increasing distance from the line. The distribution of the observed distances is used to estimate a "detection function" that describes the probability of detecting an object at a given distance. Given that various basic assumptions hold, this function allows the estimation of the average probability ''P'' of detecting an object given that is within width ''w'' of the line. Object density can then be estimated as , where ''n'' is the number of objects detected and ''a'' is the size of the region covered (total length of the transect (''L'') multiplied by 2''w'').
In summary, modeling how detectability drops off with increasing distance from the transect allows estimating how many objects there are in total in the area of interest, based on the number that were actually observed.
The survey methodology for point transects is slightly different. In this case, the observer remains stationary, the survey ends not when the end of the transect is reached but after a pre-determined time, and measured distances to the observer are used directly without conversion to transverse distances. Detection function types and fitting are also different to some degree.
Detection function
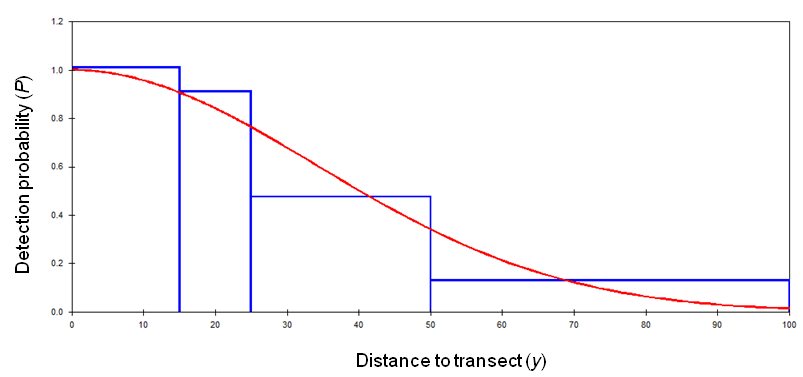
 The drop-off of detectability with increasing distance from the transect line is modeled using a detection function g(''y'') (here ''y'' is distance from the line). This function is fitted to the distribution of detection ranges represented as a
The drop-off of detectability with increasing distance from the transect line is modeled using a detection function g(''y'') (here ''y'' is distance from the line). This function is fitted to the distribution of detection ranges represented as a probability density function
In probability theory, a probability density function (PDF), density function, or density of an absolutely continuous random variable, is a Function (mathematics), function whose value at any given sample (or point) in the sample space (the s ...
(PDF). The PDF is a histogram
A histogram is a visual representation of the frequency distribution, distribution of quantitative data. To construct a histogram, the first step is to Data binning, "bin" (or "bucket") the range of values— divide the entire range of values in ...
of collected distances and describes the probability that an object at distance ''y'' will be detected by an observer on the center line, with detections on the line itself (''y'' = 0) assumed to be certain (''P'' = 1).
By preference, g(''y'') is a robust function that can represent data with unclear or weakly defined distribution characteristics, as is frequently the case in field data. Several types of functions are commonly used, depending on the general shape of the detection data's PDF:
Here ''w'' is the overall detection truncation distance and ''a'', ''b'' and ''σ'' are function-specific parameters. The half-normal and hazard-rate functions are generally considered to be most likely to represent field data that was collected under well-controlled conditions. Detection probability appearing to increase or remain constant with distance from the transect line may indicate problems with data collection or survey design.
Covariates
Series expansions
A frequently used method to improve the fit of the detection function to the data is the use of series expansions. Here, the function is split into a "key" part (of the type covered above) and a "series" part; i.e., g(''y'') = key(''y'') + series(''y'') The series generally takes the form of apolynomial
In mathematics, a polynomial is a Expression (mathematics), mathematical expression consisting of indeterminate (variable), indeterminates (also called variable (mathematics), variables) and coefficients, that involves only the operations of addit ...
(e.g. a Hermite polynomial
In mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence.
The polynomials arise in:
* signal processing as Hermitian wavelets for wavelet transform analysis
* probability, such as the Edgeworth series, as well a ...
) and is intended to add flexibility to the form of the key function, allowing it to fit more closely to the data PDF. While this can improve the precision of density/abundance estimates, its use is only defensible if the data set is of sufficient size and quality to represent a reliable estimate of detection distance distribution. Otherwise there is a risk of overfitting
In mathematical modeling, overfitting is "the production of an analysis that corresponds too closely or exactly to a particular set of data, and may therefore fail to fit to additional data or predict future observations reliably". An overfi ...
the data and allowing non-representative characteristics of the data set to bias the fitting process.
Assumptions and sources of bias
Since distance sampling is a comparatively complex survey method, the reliability of model results depends on meeting a number of basic assumptions. The most fundamental ones are listed below. Data derived from surveys that violate one or more of these assumptions can frequently, but not always, be corrected to some extent before or during analysis.Software implementations
A project group at theUniversity of St Andrews
The University of St Andrews (, ; abbreviated as St And in post-nominals) is a public university in St Andrews, Scotland. It is the List of oldest universities in continuous operation, oldest of the four ancient universities of Scotland and, f ...
maintains a suite of packages for use with R as well as a standalone program for Windows.
References
Further reading
* El-Shaarawi (ed) 'Encyclopedia of Environmetrics', Wiley-Blackwell, 2012 {{ISBN, 978-0-47097-388-2, six volume set.External links
Bibliography of > 1400 scientific publications using the method
Environmental statistics Demography Sampling techniques