Discrete tomographyHerman, G. T. and Kuba, A., Discrete Tomography: Foundations, Algorithms, and Applications, Birkhäuser Boston, 1999 Herman, G. T. and Kuba, A., Advances in Discrete Tomography and Its Applications, Birkhäuser Boston, 2007 focuses on the problem of reconstruction of

binary image A binary image is a digital image that consists of pixels that can have one of exactly two colors, usually black and white. Each pixel is stored as a single bit — i.e. either a 0 or 1. A binary image can be stored in memory as a bitmap: a p ...

s (or finite subsets of the

integer lattice In mathematics, the -dimensional integer lattice (or cubic lattice), denoted , is the lattice (group), lattice in the Euclidean space whose lattice points are tuple, -tuples of integers. The two-dimensional integer lattice is also called the s ...

) from a small number of their

projection Projection or projections may refer to: Physics * Projection (physics), the action/process of light, heat, or sound reflecting from a surface to another in a different direction * The display of images by a projector Optics, graphics, and carto ...

s. In general,

tomography Tomography is imaging by sections or sectioning that uses any kind of penetrating wave. The method is used in radiology, archaeology, biology, atmospheric science, geophysics, oceanography, plasma physics, materials science, cosmochemistry, ast ...

deals with the problem of determining shape and dimensional information of an object from a set of projections. From the mathematical point of view, the object corresponds to a

function Function or functionality may refer to: Computing * Function key, a type of key on computer keyboards * Function model, a structured representation of processes in a system * Function object or functor or functionoid, a concept of object-orie ...

and the problem posed is to reconstruct this function from its

integral In mathematics, an integral is the continuous analog of a Summation, sum, which is used to calculate area, areas, volume, volumes, and their generalizations. Integration, the process of computing an integral, is one of the two fundamental oper ...

s or sums over subsets of its

domain A domain is a geographic area controlled by a single person or organization. Domain may also refer to: Law and human geography * Demesne, in English common law and other Medieval European contexts, lands directly managed by their holder rather ...

. In general, the tomographic

inversion Inversion or inversions may refer to: Arts * ''Inversion'' (artwork), a 2005 temporary sculpture in Houston, Texas * Inversion (music), a term with various meanings in music theory and musical set theory * ''Inversions'' (novel) by Iain M. Bank ...

problem may be continuous or discrete. In continuous tomography both the domain and the range of the function are continuous and line integrals are used. In discrete tomography the domain of the function may be either discrete or continuous, and the range of the function is a finite set of real, usually nonnegative numbers. In continuous tomography when a large number of projections is available, accurate reconstructions can be made by many different algorithms. It is typical for discrete tomography that only a few projections (line sums) are used. In this case, conventional techniques all fail. A special case of discrete tomography deals with the problem of the reconstruction of a binary image from a small number of projections. The name ''discrete tomography'' is due to Larry Shepp, who organized the first meeting devoted to this topic (

DIMACS The Center for Discrete Mathematics and Theoretical Computer Science (DIMACS) is a collaboration between Rutgers University, Princeton University, and the research firms AT&T, Bell Labs, Applied Communication Sciences, and NEC. It was founded in ...

Mini-Symposium on Discrete Tomography, September 19, 1994,

Rutgers University Rutgers University ( ), officially Rutgers, The State University of New Jersey, is a Public university, public land-grant research university consisting of three campuses in New Jersey. Chartered in 1766, Rutgers was originally called Queen's C ...

Theory

Discrete tomography has strong connections with other mathematical fields, such as

number theory Number theory is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic functions. Number theorists study prime numbers as well as the properties of mathematical objects constructed from integers (for example ...

,R.J. Gardner, P. Gritzmann, Discrete tomography: determination of finite sets by X-rays, Trans. Amer. Math. Soc. 349 (1997), no. 6, 2271-2295.L. Hajdu, R. Tijdeman
Algebraic aspects of discrete tomography
J. reine angew. Math. 534 (2001), 119-128.A. Alpers, R. Tijdeman, The Two-Dimensional Prouhet-Tarry-Escott Problem, Journal of Number Theory, 123 (2), pp. 403-412, 200

discrete mathematics Discrete mathematics is the study of mathematical structures that can be considered "discrete" (in a way analogous to discrete variables, having a bijection with the set of natural numbers) rather than "continuous" (analogously to continuous f ...

,S. Brunetti, A. Del Lungo, P. Gritzmann, S. de Vries
On the reconstruction of binary and permutation matrices under (binary) tomographic constraints
Theoret. Comput. Sci. 406 (2008), no. 1-2, 63-71.A. Alpers, P. Gritzmann, On Stability, Error Correction, and Noise Compensation in Discrete Tomography, SIAM Journal on Discrete Mathematics 20 (1), pp. 227-239, 200

/ref>P. Gritzmann, B. Langfeld, On the index of Siegel grids and its application to the tomography of quasicrystals. European J. Combin. 29 (2008), no. 8, 1894-1909.

computational complexity theory In theoretical computer science and mathematics, computational complexity theory focuses on classifying computational problems according to their resource usage, and explores the relationships between these classifications. A computational problem ...

R.J. Gardner, P. Gritzmann, D. Prangenberg
On the computational complexity of reconstructing lattice sets from their X-rays
Discrete Math. 202 (1999), no. 1-3, 45-71.C. Dürr, F. Guiñez, M. Matamala
Reconstructing 3-Colored Grids from Horizontal and Vertical Projections Is NP-hard
ESA 2009: 776-787. and

combinatorics Combinatorics is an area of mathematics primarily concerned with counting, both as a means and as an end to obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many ...

.H.J. Ryser, Matrices of zeros and ones, Bull. Amer. Math. Soc. 66 1960 442-464.D. Gale
A theorem on flows in networks
Pacific J. Math. 7 (1957), 1073-1082.E. Barcucci, S. Brunetti, A. Del Lungo, M. Nivat
Reconstruction of lattice sets from their horizontal, vertical and diagonal X-rays
Discrete Mathematics 241(1-3): 65-78 (2001). In fact, a number of discrete tomography problems were first discussed as combinatorial problems. In 1957,

H. J. Ryser Herbert John Ryser (July 28, 1923 – July 12, 1985) was a professor of mathematics, widely regarded as one of the major figures in combinatorics in the 20th century.David Gale David Gale (December 13, 1921 – March 7, 2008) was an American mathematician and economist. He was a professor emeritus at the University of California, Berkeley, affiliated with the departments of mathematics, economics, and industrial ...

found the same consistency conditions, but in connection with the network flow problem. Another result of Ryser's is the definition of the switching operation by which discrete sets having the same projections can be transformed into each other. The problem of reconstructing a binary image from a small number of projections generally leads to a large number of solutions. It is desirable to limit the class of possible solutions to only those that are typical of the class of the images which contains the image being reconstructed by using a priori information, such as convexity or connectedness.

Theorems

* Reconstructing (finite) planar lattice sets from their 1-dimensional X-rays is an

NP-hard In computational complexity theory, a computational problem ''H'' is called NP-hard if, for every problem ''L'' which can be solved in non-deterministic polynomial-time, there is a polynomial-time reduction from ''L'' to ''H''. That is, assumi ...

problem if the X-rays are taken from

m\geq 3

lattice directions (for

m=2

the problem is in P). * The reconstruction problem is highly unstable for

m\geq 3

(meaning that a small perturbation of the X-rays may lead to completely different reconstructions) and stable for

m=2

, see.A. Alpers, P. Gritzmann, L. Thorens
Stability and Instability in Discrete Tomography
Lecture Notes in Computer Science 2243; Digital and Image Geometry (Advanced Lectures), G. Bertrand, A. Imiya, R. Klette (Eds.), pp. 175-186, Springer-Verlag, 2001.A. Alpers, S. Brunetti
On the Stability of Reconstructing Lattice Sets from X-rays Along Two Directions
Lecture Notes in Computer Science 3429; Digital Geometry for Computer Imagery, E. Andres, G. Damiand, P. Lienhardt (Eds.), pp. 92-103, Springer-Verlag, 2005.B. van Dalen
Stability results for uniquely determined sets from two directions in discrete tomography
Discrete Mathematics 309(12): 3905-3916 (2009). * Coloring a grid using

k

colors with the restriction that each row and each column has a specific number of cells of each color is known as the

(k-1)

−atom problem in the discrete tomography community. The problem is NP-hard for

k \geq 3

, see. For further results, see

Algorithms

Among the reconstruction methods one can find

algebraic reconstruction technique frame, Animated sequence of reconstruction steps, one iteration. The algebraic reconstruction technique (ART) is an iterative reconstruction technique used in computed tomography. It reconstructs an image from a series of angular projections (a ...

s (e.g., DART or K. J. Batenburg, and J. Sijbers, "Generic iterative subset algorithms for discrete tomography", Discrete Applied Mathematics, vol. 157, no. 3, pp. 438-451, 2009),

greedy algorithm A greedy algorithm is any algorithm that follows the problem-solving heuristic of making the locally optimal choice at each stage. In many problems, a greedy strategy does not produce an optimal solution, but a greedy heuristic can yield locally ...

s (see P. Gritzmann, S. de Vries, M. Wiegelmann
Approximating binary images from discrete X-rays
SIAM J. Optim. 11 (2000), no. 2, 522-546. for approximation guarantees), and

Monte Carlo algorithm In computing, a Monte Carlo algorithm is a randomized algorithm whose output may be incorrect with a certain (typically small) probability. Two examples of such algorithms are the Karger–Stein algorithm and the Monte Carlo algorithm for mini ...

Applications

Various algorithms have been applied in

image processing An image or picture is a visual representation. An image can be two-dimensional, such as a drawing, painting, or photograph, or three-dimensional, such as a carving or sculpture. Images may be displayed through other media, including a pr ...

, Batenburg, Joost; Sijbers, Jan - DART: A practical reconstruction algorithm for discrete tomography - In: IEEE transactions on image processing, Vol. 20, Nr. 9, p. 2542-2553, (2011).

medicine Medicine is the science and Praxis (process), practice of caring for patients, managing the Medical diagnosis, diagnosis, prognosis, Preventive medicine, prevention, therapy, treatment, Palliative care, palliation of their injury or disease, ...

, three-dimensional statistical data security problems, computer tomograph assisted engineering and design,

electron microscopy An electron microscope is a microscope that uses a beam of electrons as a source of illumination. It uses electron optics that are analogous to the glass lenses of an optical light microscope to control the electron beam, for instance focusing i ...

S. Bals, K. J. Batenburg, J. Verbeeck, J. Sijbers, and G. Van Tendeloo, "Quantitative 3D reconstruction of catalyst particles for bamboo-like carbon-nanotubes", Nano Letters, Vol. 7, Nr. 12, p. 3669-3674, (2007) Batenburg J., S. Bals, Sijbers J., C. Kubel, P.A. Midgley, J.C. Hernandez, U. Kaiser, E.R. Encina, E.A. Coronado, and G. Van Tendeloo, "3D imaging of nanomaterials by discrete tomography", Ultramicroscopy, Vol. 109, p. 730-740, (2009) and

materials science Materials science is an interdisciplinary field of researching and discovering materials. Materials engineering is an engineering field of finding uses for materials in other fields and industries. The intellectual origins of materials sci ...

, including the 3DXRD microscope.A. Alpers, H.F. Poulsen, E. Knudsen, G.T. Herman, A Discrete Tomography Algorithm for Improving the Quality of 3DXRD Grain Maps, Journal of Applied Crystallography 39, pp. 582-588, 200

L. Rodek, H.F. Poulsen, E. Knudsen, G.T. Herman
A stochastic algorithm for reconstruction of grain maps of moderately deformed specimens based on X-ray diffraction
Journal of Applied Crystallography 40:313-321, 2007.K. J. Batenburg, J. Sijbers, H. F. Poulsen, and E. Knudsen, "DART: A Robust Algorithm for Fast Reconstruction of 3D Grain Maps", Journal of Applied Crystallography, vol. 43, pp. 1464-1473, 2010 A form of discrete tomography also forms the basis of

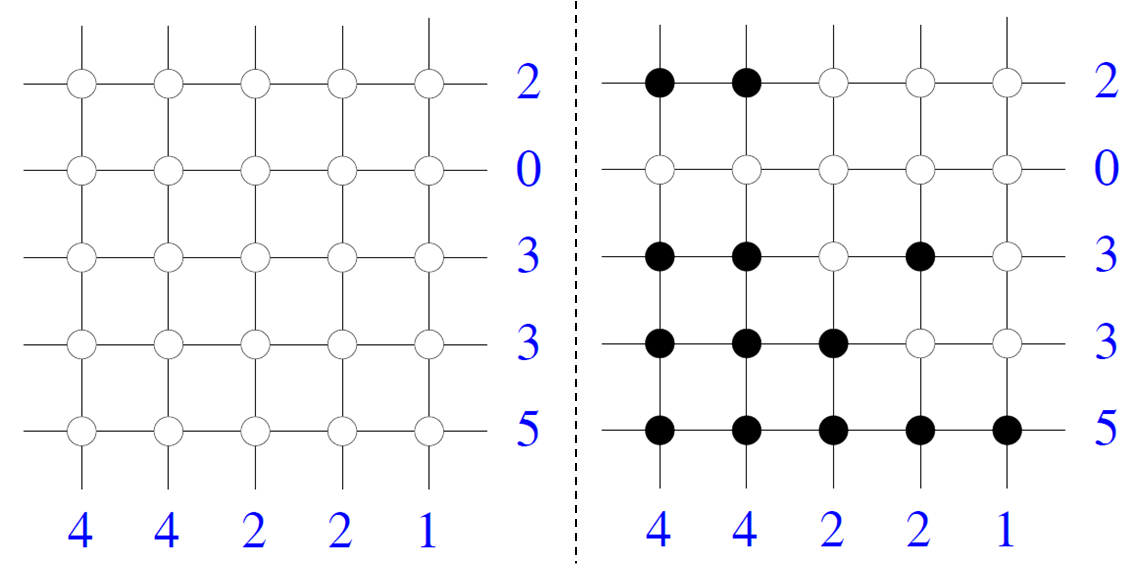
nonogram Nonograms, also known as Hanjie, Paint by Numbers, Griddlers, Pic-a-Pix, and Picross, are picture logic puzzles in which cells in a grid must be colored or left blank according to numbers at the edges of the grid to reveal a hidden picture. In ...

s, a type of

logic puzzle A logic puzzle is a puzzle deriving from the mathematics, mathematical field of deductive reasoning, deduction. History The logic puzzle was first produced by Charles Lutwidge Dodgson, who is better known under his pen name Lewis Carroll, the a ...

in which information about the rows and columns of a digital image is used to reconstruct the image.

References

External links

Euro DT (a Discrete Tomography Wiki site for researchers)

Tomography applet by Christoph Dürr

PhD thesis on discrete tomography (2012): Tomographic segmentation and discrete tomography for quantitative analysis of transmission tomography data
{{Authority control Applied mathematics Digital geometry