Derived Row on:
[Wikipedia]
[Google]
[Amazon]
In
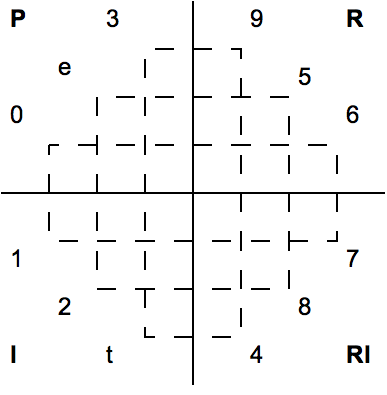
 P represents the original trichord, RI, retrograde and inversion, R retrograde, and I inversion.
The entire row, if B=0, is:
*0, 11, 3, 4, 8, 7, 9, 5, 6, 1, 2, 10.
For instance, the third trichord:
*9, 5, 6
is the first trichord:
*0, 11, 3
backwards:
*3, 11, 0
and transposed 6
*3+6, 11+6, 0+6 = 9, 5, 6 mod 12.
Combinatoriality is often a result of derived rows. For example, the Op. 24 row is all-combinatorial, P0 being hexachordally combinatorial with P6, R0, I5, and RI11.
P represents the original trichord, RI, retrograde and inversion, R retrograde, and I inversion.
The entire row, if B=0, is:
*0, 11, 3, 4, 8, 7, 9, 5, 6, 1, 2, 10.
For instance, the third trichord:
*9, 5, 6
is the first trichord:
*0, 11, 3
backwards:
*3, 11, 0
and transposed 6
*3+6, 11+6, 0+6 = 9, 5, 6 mod 12.
Combinatoriality is often a result of derived rows. For example, the Op. 24 row is all-combinatorial, P0 being hexachordally combinatorial with P6, R0, I5, and RI11.
music
Music is generally defined as the The arts, art of arranging sound to create some combination of Musical form, form, harmony, melody, rhythm or otherwise Musical expression, expressive content. Exact definition of music, definitions of mu ...
using the twelve-tone technique
The twelve-tone technique—also known as dodecaphony, twelve-tone serialism, and (in British usage) twelve-note composition—is a method of musical composition first devised by Austrian composer Josef Matthias Hauer, who published his "law ...
, derivation is the construction of a row through segments. A derived row is a tone row
In music, a tone row or note row (german: Reihe or '), also series or set, is a non-repetitive ordering of a set of pitch-classes, typically of the twelve notes in musical set theory of the chromatic scale, though both larger and smaller sets ...
whose entirety of twelve tones is constructed from a segment or portion of the whole, the generator. Anton Webern
Anton Friedrich Wilhelm von Webern (3 December 188315 September 1945), better known as Anton Webern (), was an Austrian composer and conductor whose music was among the most radical of its milieu in its sheer concision, even aphorism, and ste ...
often used derived rows in his pieces. A partition is a segment created from a set through partitioning.
Derivation
Rows may be derived from a sub- set of any number ofpitch class
In music, a pitch class (p.c. or pc) is a set of all pitches that are a whole number of octaves apart; for example, the pitch class C consists of the Cs in all octaves. "The pitch class C stands for all possible Cs, in whatever octave positi ...
es that is a divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer m that may be multiplied by some integer to produce n. In this case, one also says that n is a multiple of m. An integer n is divisible or evenly divisible by ...
of 12, the most common being the first three pitches or a trichord
In music theory, a trichord () is a group of three different pitch classes found within a larger group. A trichord is a contiguous three-note set from a musical scale or a twelve-tone row.
In musical set theory there are twelve trichords g ...
. This segment may then undergo transposition, inversion
Inversion or inversions may refer to:
Arts
* , a French gay magazine (1924/1925)
* ''Inversion'' (artwork), a 2005 temporary sculpture in Houston, Texas
* Inversion (music), a term with various meanings in music theory and musical set theory
* ...
, retrograde, or any combination to produce the other parts of the row (in this case, the other three segments).
One of the side effects of derived rows is invariance
Invariant and invariance may refer to:
Computer science
* Invariant (computer science), an expression whose value doesn't change during program execution
** Loop invariant, a property of a program loop that is true before (and after) each iterat ...
. For example, since a segment may be equivalent to the generating segment inverted and transposed, say, 6 semitone
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically.
It is defined as the interval between two adjacent no ...
s, when the entire row is inverted and transposed six semitones the generating segment will now consist of the pitch classes of the derived segment.
Here is a row derived from a trichord
In music theory, a trichord () is a group of three different pitch classes found within a larger group. A trichord is a contiguous three-note set from a musical scale or a twelve-tone row.
In musical set theory there are twelve trichords g ...
taken from Webern
Anton Friedrich Wilhelm von Webern (3 December 188315 September 1945), better known as Anton Webern (), was an Austrian composer and conductor whose music was among the most radical of its milieu in its sheer concision, even aphorism, and stea ...
's Concerto, Op. 24:
:
Partition and mosaic
The opposite is partitioning, the use of methods to create segments from entire sets, most often through registral difference. In music using thetwelve-tone technique
The twelve-tone technique—also known as dodecaphony, twelve-tone serialism, and (in British usage) twelve-note composition—is a method of musical composition first devised by Austrian composer Josef Matthias Hauer, who published his "law ...
a partition is "a collection of disjunct, unordered pitch-class sets that comprise an aggregate
Aggregate or aggregates may refer to:
Computing and mathematics
* collection of objects that are bound together by a root entity, otherwise known as an aggregate root. The aggregate root guarantees the consistency of changes being made within the ...
". It is a method of creating segments from sets, most often through registral difference, the opposite of derivation used in derived rows.
More generally, in musical set theory partitioning is the division of the domain of pitch class sets into types, such as transpositional type, see equivalence class
In mathematics, when the elements of some set S have a notion of equivalence (formalized as an equivalence relation), then one may naturally split the set S into equivalence classes. These equivalence classes are constructed so that elements ...
and cardinality
In mathematics, the cardinality of a set is a measure of the number of elements of the set. For example, the set A = \ contains 3 elements, and therefore A has a cardinality of 3. Beginning in the late 19th century, this concept was generalized ...
.
Partition is also an old name for types of compositions in several parts; there is no fixed meaning, and in several cases the term was reportedly interchanged with various other terms.
A cross-partition is, "a two-dimensional configuration of pitch classes whose columns are realized as chords, and whose rows are differentiated from one another by registral, timbral, or other means.": "...more accurately described by ''permutation'' rather than ''rotation''. Permutations, of course, include the set of possible rotations." This allows, "''slot-machine'' transformations that reorder the vertical trichords but keep the pitch classes in their columns."
A mosaic is "a partition that divides the aggregate into segments of equal size", according to Martino (1961). "Kurth 1992 and Mead 1988 use ''mosaic'' and ''mosaic class'' in the way that I use ''partition'' and ''mosaic''", are used here. However later, he says that, "the DS determines the number of distinct partitions in a ''mosaic'', which is the set of partitions related by transposition and inversion."
Inventory
The first useful characteristic of a partition, an inventory, is the set classes produced by the union of the constituentpitch class
In music, a pitch class (p.c. or pc) is a set of all pitches that are a whole number of octaves apart; for example, the pitch class C consists of the Cs in all octaves. "The pitch class C stands for all possible Cs, in whatever octave positi ...
sets of a partition. For trichord
In music theory, a trichord () is a group of three different pitch classes found within a larger group. A trichord is a contiguous three-note set from a musical scale or a twelve-tone row.
In musical set theory there are twelve trichords g ...
s and hexachord
In music, a hexachord (also hexachordon) is a six-note series, as exhibited in a scale ( hexatonic or hexad) or tone row. The term was adopted in this sense during the Middle Ages and adapted in the 20th century in Milton Babbitt's serial theor ...
s combined see Alegant 1993, Babbitt 1955, Dubiel 1990, Mead 1994, Morris and Alegant 1988, Morris 1987, and Rouse 1985.
Degree of symmetry
The second useful characteristic of a partition, the degree of symmetry (DS), "specifies the number of operations that preserve the unordered pcsets of a partition; it tells the extent to which that partition's pitch-class sets map into (or onto) each other under transposition or inversion."References
Sources * {{Twelve-tone technique Twelve-tone technique