Dehn Twist

In geometric topology, a branch of mathematics, a Dehn twist is a certain type of self-homeomorphism of a surface (two-dimensional manifold).

Definition

Suppose that ''c'' is a simple closed curve in a closed, orientable surface ''S''. Let ''A'' be a tubular neighborhood of ''c''. Then ''A'' is an annulus, homeomorphic to the Cartesian product of a circle and a unit interval ''I'':

:$c \subset A \cong S^1 \times I.$

Give ''A'' coordinates (''s'', ''t'') where ''s'' is a complex number of the form $e^$ with \theta \in , 2\pi and .

Let ''f'' be the map from ''S'' to itself which is the identity outside of ''A'' and inside ''A'' we have

:$f(s, t) = \left(se^, t\right).$

Then ''f'' is a Dehn twist about the curve ''c''.

Dehn twists can also be defined on a non-orientable surface ''S'', provided one starts with a 2-sided simple closed curve ''c'' on ''S''.

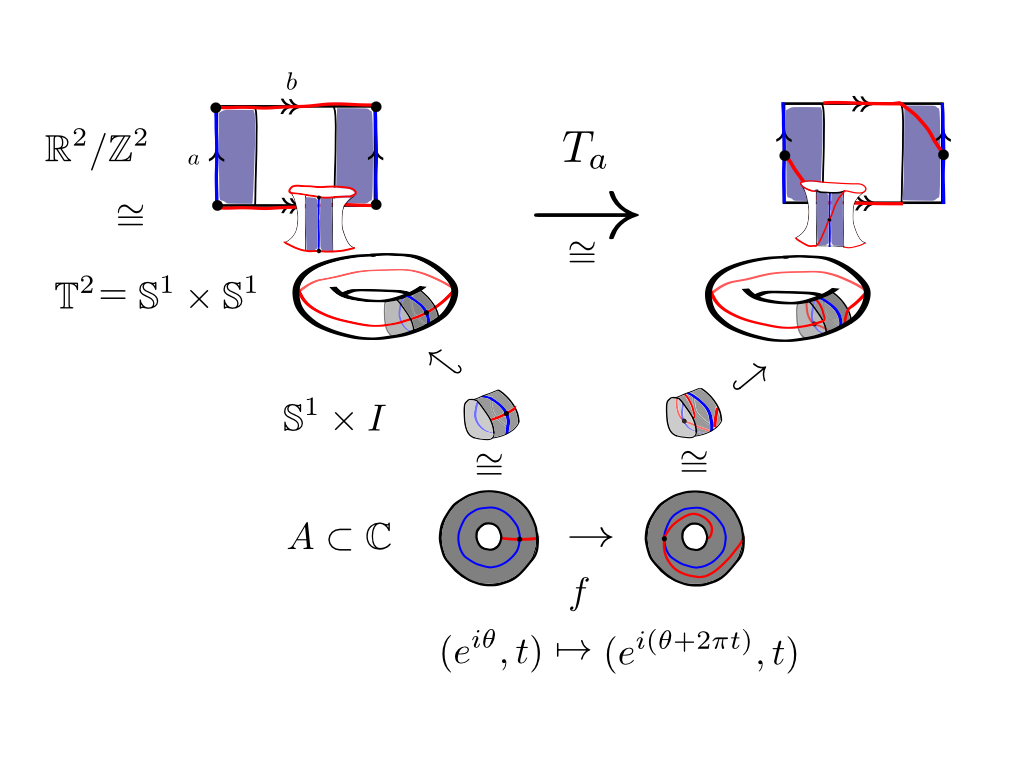
Example

Consider the torus represented by a fundamental polygon with edges ''a'' and ''b''

:$\mathbb^2 \cong \mathbb^2/\mathbb^2.$

Let a closed curve be the line along the edge ''a'' called $\gamma_a$.

Given the choice of gluing homeomorphism in the figure, a tubular neighborhood of the curve $\gamma_a$ will look like a band linked around a doughnut. This neighborhood is homeomorphic to an annulus, say
:$a(0; 0, 1) = \$

in the complex plane.

By extending to the torus the twisting map $\left(e^, t\right) \mapsto \left(e^, t\right)$ of the annulus, through the homeomorphisms of the annulus to an open cylinder to the neighborhood of $\gamma_a$, yields a Dehn twist of the torus by ''a''.

:$T_a: \mathbb^2 \to \mathbb^2$

This self homeomorphism acts on the closed curve along ''b''. In the tubular neighborhood it takes the curve of ''b'' once along the curve of ''a''.

A homeomorphism between topological spaces induces a natural isomorphism between their fundamental groups. Therefore one has an automorphism

:_\ast: \pi_1\left(\mathbb^2\right) \to \pi_1\left(\mathbb^2\right): \mapsto \left _a(x)\right/math>

where 'x''are the homotopy classes of the closed curve ''x'' in the torus. Notice _\ast( = /math> and _\ast( = *a/math>, where $b*a$ is the path travelled around ''b'' then ''a''.

Mapping class group

It is a theorem of Max Dehn that maps of this form generate the mapping class group of isotopy classes of orientation-preserving homeomorphisms of any closed, oriented genus-$g$ surface. W. B. R. Lickorish later rediscovered this result with a simpler proof and in addition showed that Dehn twists along $3g - 1$ explicit curves generate the mapping class group (this is called by the punning name "Lickorish twist theorem"); this number was later improved by Stephen P. Humphries to $2g + 1$, for $g > 1$, which he showed was the minimal number.

Lickorish also obtained an analogous result for non-orientable surfaces, which require not only Dehn twists, but also "Y-homeomorphisms."

See also

* Lantern relation

References

* Andrew J. Casson, Steven A Bleiler, ''Automorphisms of Surfaces After Nielsen and Thurston'', Cambridge University Press, 1988. .
* Stephen P. Humphries, "Generators for the mapping class group," in: ''Topology of low-dimensional manifolds'' (''Proc. Second Sussex Conf.'', Chelwood Gate, 1977), pp. 44–47, Lecture Notes in Math., 722, Springer, Berlin, 1979.
* W. B. R. Lickorish, "A representation of orientable combinatorial 3-manifolds." ''Ann. of Math.'' (2) 76 1962 531—540.
* W. B. R. Lickorish, "A finite set of generators for the homotopy group of a 2-manifold", ''Proc. Cambridge Philos. Soc.'' 60 (1964), 769–778. {{MR, 0171269

Geometric topology
Homeomorphisms