geometry Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...

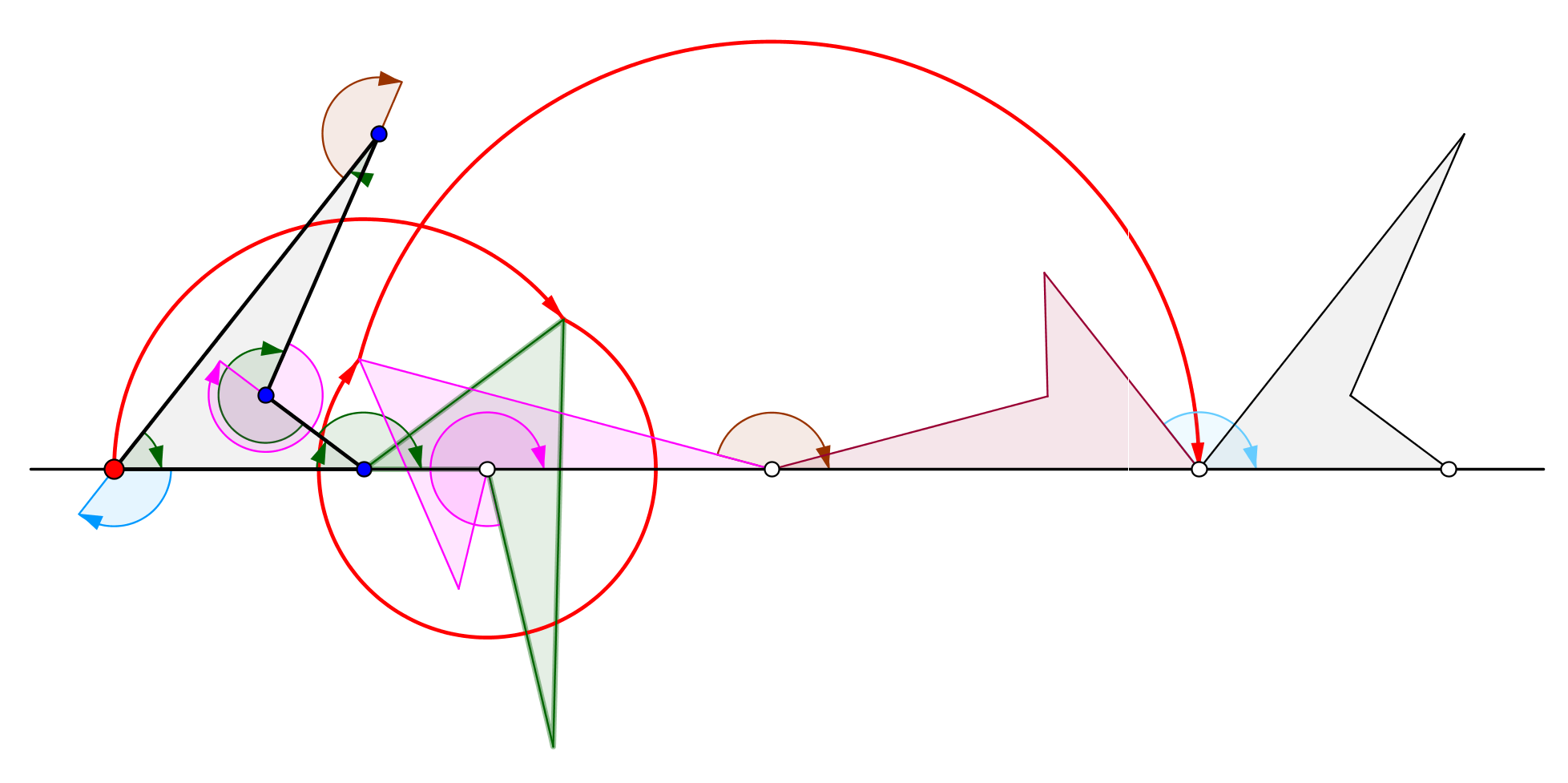
, a cyclogon is the

curve In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight. Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ...

traced by a vertex of a

regular polygon In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either ''convex ...

that

rolls Rolls may refer to: People * Charles Rolls (engraver) (1799–1885), engraver * Charles Rolls (1877–1910), Welsh motoring and aviation pioneer, co-founder of Rolls-Royce Limited * John Etherington Welch Rolls (1807–1870), British jurist and art ...

without slipping along a

straight line In geometry, a straight line, usually abbreviated line, is an infinitely long object with no width, depth, or curvature, an idealization of such physical objects as a straightedge, a taut string, or a ray of light. Lines are spaces of dimens ...

. In the limit, as the number of sides increases to infinity, the cyclogon becomes a

cycloid In geometry, a cycloid is the curve traced by a point on a circle as it Rolling, rolls along a Line (geometry), straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette (curve), roulette, a curve g ...

. The cyclogon has an interesting property regarding its area. Let denote the area of the region above the line and below one of the arches, let denote the area of the rolling polygon, and let denote the area of the disk that circumscribes the polygon. For every cyclogon generated by a regular polygon, :

A = P + 2C. \,

Examples

Cyclogons generated by an equilateral triangle and a square

Prolate cyclogon generated by an equilateral triangle

Curtate cyclogon generated by an equilateral triangle

Cyclogons generated by quadrilaterals

Cyclogon_generated_by_a_non-convex_quadrilateral

Cyclogon_generated_by_a_convex_quadrilateral

Cyclogon_generated_by_a_star-like_quadrilateral

Generalized cyclogons

A cyclogon is obtained when a polygon rolls over a straight line. Let it be assumed that the regular polygon rolls over the edge of another polygon. Let it also be assumed that the tracing point is not a point on the boundary of the polygon but possibly a point within the polygon or outside the polygon but lying in the plane of the polygon. In this more general situation, let a curve be traced by a point z on a regular polygonal disk with n sides rolling around another regular polygonal disk with m sides. The edges of the two regular polygons are assumed to have the same length. A point z attached rigidly to the n-gon traces out an arch consisting of n circular arcs before repeating the pattern periodically. This curve is called a trochogon — an ''epitrochogon'' if the n-gon rolls outside the m-gon, and a ''hypotrochogon'' if it rolls inside the m-gon. The trochogon is curtate if z is inside the n-gon, and prolate (with loops) if z is outside the n-gon. If z is at a vertex it traces an epicyclogon or a hypocyclogon.

References

{{Reflist Roulettes (curve) Piecewise-circular curves