Crystallographic point group on:
[Wikipedia]
[Google]
[Amazon]
In
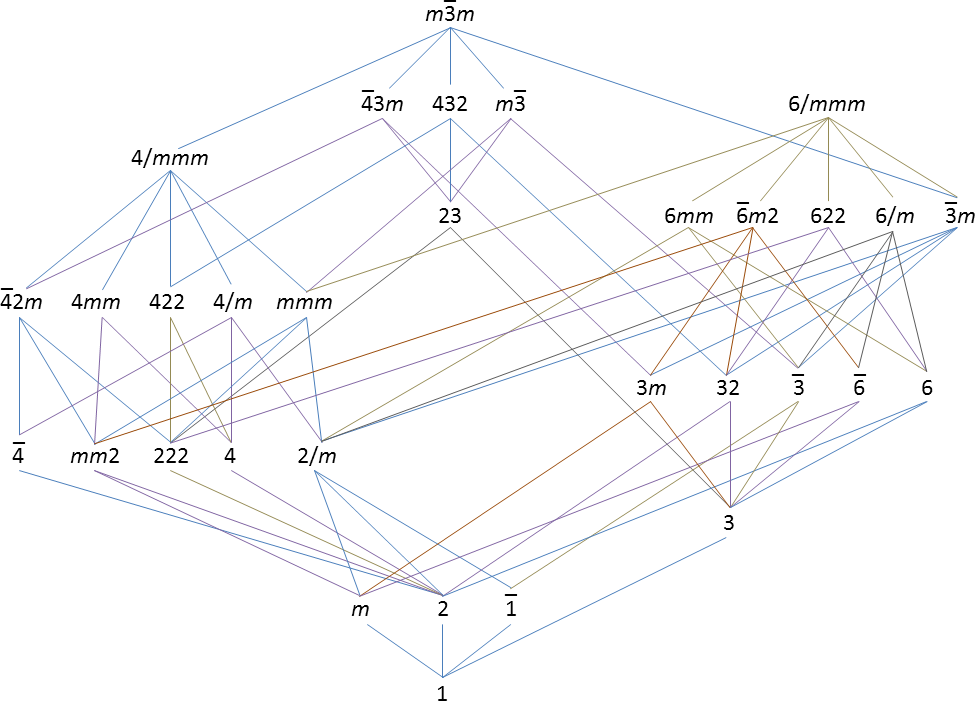 An abbreviated form of the
An abbreviated form of the
Point-group symbols in International Tables for Crystallography (2006). Vol. A, ch. 12.1, pp. 818-820Names and symbols of the 32 crystal classes in International Tables for Crystallography (2006). Vol. A, ch. 10.1, p. 794
{{Crystal systems Symmetry Crystallography Discrete groups
crystallography
Crystallography is the experimental science of determining the arrangement of atoms in crystalline solids. Crystallography is a fundamental subject in the fields of materials science and solid-state physics (condensed matter physics). The wo ...
, a crystallographic point group is a set of symmetry operation In group theory, geometry, representation theory and molecular symmetry, a symmetry operation is a transformation of an object that leaves an object looking the same after it has been carried out. For example, as transformations of an object in spac ...
s, corresponding to one of the point groups in three dimensions
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O(3), the group of all isometries t ...
, such that each operation (perhaps followed by a translation
Translation is the communication of the Meaning (linguistic), meaning of a #Source and target languages, source-language text by means of an Dynamic and formal equivalence, equivalent #Source and target languages, target-language text. The ...
) would leave the structure of a crystal unchanged i.e. the same kinds of atoms would be placed in similar positions as before the transformation. For example, in many crystals in the cubic crystal system, a rotation of the unit cell by 90 degrees around an axis that is perpendicular to one of the faces of the cube is a symmetry operation that moves each atom to the location of another atom of the same kind, leaving the overall structure of the crystal unaffected.
In the classification of crystals, each point group defines a so-called (geometric) crystal class. There are infinitely many three-dimensional point group
In geometry, a point group is a mathematical group of symmetry operations ( isometries in a Euclidean space) that have a fixed point in common. The coordinate origin of the Euclidean space is conventionally taken to be a fixed point, and every ...
s. However, the crystallographic restriction on the general point groups results in there being only 32 crystallographic point groups. These 32 point groups are one-and-the-same as the 32 types of morphological (external) crystalline symmetries derived in 1830 by Johann Friedrich Christian Hessel from a consideration of observed crystal forms.
The point group of a crystal determines, among other things, the directional variation of physical properties that arise from its structure, including optical properties such as birefringency, or electro-optical features such as the Pockels effect
The Pockels effect or Pockels electro-optic effect, named after Friedrich Carl Alwin Pockels (who studied the effect in 1893), changes or produces birefringence in an optical medium induced by an electric field. In the Pockels effect, also known ...
. For a periodic crystal (as opposed to a quasicrystal
A quasiperiodic crystal, or quasicrystal, is a structure that is ordered but not periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks translational symmetry. While crystals, according to the classical ...
), the group must maintain the three-dimensional translational symmetry
In geometry, to translate a geometric figure is to move it from one place to another without rotating it. A translation "slides" a thing by .
In physics and mathematics, continuous translational symmetry is the invariance of a system of equatio ...
that defines crystallinity.
Notation
The point groups are named according to their component symmetries. There are several standard notations used by crystallographers,mineralogist
Mineralogy is a subject of geology specializing in the scientific study of the chemistry, crystal structure, and physical (including optical) properties of minerals and mineralized artifacts. Specific studies within mineralogy include the proces ...
s, and physicists
A physicist is a scientist who specializes in the field of physics, which encompasses the interactions of matter and energy at all length and time scales in the physical universe.
Physicists generally are interested in the root or ultimate caus ...
.
For the correspondence of the two systems below, see crystal system
In crystallography, a crystal system is a set of point groups (a group of geometric symmetries with at least one fixed point). A lattice system is a set of Bravais lattices. Space groups are classified into crystal systems according to their poi ...
.
Schoenflies notation
In Schoenflies notation, point groups are denoted by a letter symbol with a subscript. The symbols used in crystallography mean the following: *''Cn'' (for cyclic) indicates that the group has an ''n''-fold rotation axis. ''Cnh'' is ''Cn'' with the addition of a mirror (reflection) plane perpendicular to the axis of rotation. ''Cnv'' is ''Cn'' with the addition of n mirror planes parallel to the axis of rotation. *''S2n'' (for ''Spiegel'', German formirror
A mirror or looking glass is an object that Reflection (physics), reflects an image. Light that bounces off a mirror will show an image of whatever is in front of it, when focused through the lens of the eye or a camera. Mirrors reverse the ...
) denotes a group with only a ''2n''-fold rotation-reflection axis
In geometry, an improper rotation,. also called rotation-reflection, rotoreflection, rotary reflection,. or rotoinversion is an isometry in Euclidean space that is a combination of a rotation about an axis and a reflection in a plane perpendicul ...
.
*''Dn'' (for dihedral, or two-sided) indicates that the group has an ''n''-fold rotation axis plus ''n'' twofold axes perpendicular to that axis. ''Dnh'' has, in addition, a mirror plane perpendicular to the ''n''-fold axis. ''Dnd'' has, in addition to the elements of ''Dn'', mirror planes parallel to the ''n''-fold axis.
*The letter ''T'' (for tetrahedron
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ...
) indicates that the group has the symmetry of a tetrahedron. ''Td'' includes improper rotation
In geometry, an improper rotation,. also called rotation-reflection, rotoreflection, rotary reflection,. or rotoinversion is an isometry in Euclidean space that is a combination of a rotation about an axis and a reflection in a plane perpendic ...
operations, ''T'' excludes improper rotation operations, and ''Th'' is ''T'' with the addition of an inversion.
*The letter ''O'' (for octahedron
In geometry, an octahedron (plural: octahedra, octahedrons) is a polyhedron with eight faces. The term is most commonly used to refer to the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at e ...
) indicates that the group has the symmetry of an octahedron (or cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross.
The cube is the on ...
), with (''Oh'') or without (''O'') improper operations (those that change handedness).
Due to the crystallographic restriction theorem, ''n'' = 1, 2, 3, 4, or 6 in 2- or 3-dimensional space.
''D4d'' and ''D6d'' are actually forbidden because they contain improper rotation
In geometry, an improper rotation,. also called rotation-reflection, rotoreflection, rotary reflection,. or rotoinversion is an isometry in Euclidean space that is a combination of a rotation about an axis and a reflection in a plane perpendic ...
s with n=8 and 12 respectively. The 27 point groups in the table plus ''T'', ''Td'', ''Th'', ''O'' and ''Oh'' constitute 32 crystallographic point groups.
Hermann–Mauguin notation
 An abbreviated form of the
An abbreviated form of the Hermann–Mauguin notation
In geometry, Hermann–Mauguin notation is used to represent the symmetry elements in point groups, plane groups and space groups. It is named after the German crystallographer Carl Hermann (who introduced it in 1928) and the French mineralogist ...
commonly used for space group
In mathematics, physics and chemistry, a space group is the symmetry group of an object in space, usually in three dimensions. The elements of a space group (its symmetry operations) are the rigid transformations of an object that leave it ...
s also serves to describe crystallographic point groups. Group names are
The correspondence between different notations
Isomorphisms
Many of the crystallographic point groups share the same internal structure. For example, the point groups , 2, and m contain different geometric symmetry operations, (inversion, rotation, and reflection, respectively) but all share the structure of thecyclic group
In group theory, a branch of abstract algebra in pure mathematics, a cyclic group or monogenous group is a group, denoted C''n'', that is generated by a single element. That is, it is a set of invertible elements with a single associative bi ...
C2. All isomorphic groups are of the same order
Order, ORDER or Orders may refer to:
* Categorization, the process in which ideas and objects are recognized, differentiated, and understood
* Heterarchy, a system of organization wherein the elements have the potential to be ranked a number of d ...
, but not all groups of the same order are isomorphic. The point groups which are isomorphic are shown in the following table:
This table makes use of cyclic group
In group theory, a branch of abstract algebra in pure mathematics, a cyclic group or monogenous group is a group, denoted C''n'', that is generated by a single element. That is, it is a set of invertible elements with a single associative bi ...
s (C1, C2, C3, C4, C6), dihedral groups (D2, D3, D4, D6), one of the alternating group
In mathematics, an alternating group is the group of even permutations of a finite set. The alternating group on a set of elements is called the alternating group of degree , or the alternating group on letters and denoted by or
Basic pr ...
s (A4), and one of the symmetric group
In abstract algebra, the symmetric group defined over any set is the group whose elements are all the bijections from the set to itself, and whose group operation is the composition of functions. In particular, the finite symmetric group ...
s (S4). Here the symbol " × " indicates a direct product
In mathematics, one can often define a direct product of objects already known, giving a new one. This generalizes the Cartesian product of the underlying sets, together with a suitably defined structure on the product set. More abstractly, one t ...
.
Deriving the crystallographic point group (crystal class) from the space group
# Leave out theBravais lattice
In geometry and crystallography, a Bravais lattice, named after , is an infinite array of discrete points generated by a set of discrete translation operations described in three dimensional space by
: \mathbf = n_1 \mathbf_1 + n_2 \mathbf_2 + n ...
type.
# Convert all symmetry elements with translational components into their respective symmetry elements without translation symmetry. (Glide planes are converted into simple mirror planes; screw axes are converted into simple axes of rotation.)
# Axes of rotation, rotoinversion axes, and mirror planes remain unchanged.
See also
*Molecular symmetry
Molecular symmetry in chemistry describes the symmetry present in molecules and the classification of these molecules according to their symmetry. Molecular symmetry is a fundamental concept in chemistry, as it can be used to predict or explain ...
* Point group
In geometry, a point group is a mathematical group of symmetry operations ( isometries in a Euclidean space) that have a fixed point in common. The coordinate origin of the Euclidean space is conventionally taken to be a fixed point, and every ...
* Space group
In mathematics, physics and chemistry, a space group is the symmetry group of an object in space, usually in three dimensions. The elements of a space group (its symmetry operations) are the rigid transformations of an object that leave it ...
* Point groups in three dimensions
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O(3), the group of all isometries t ...
* Crystal system
In crystallography, a crystal system is a set of point groups (a group of geometric symmetries with at least one fixed point). A lattice system is a set of Bravais lattices. Space groups are classified into crystal systems according to their poi ...
References
External links
Point-group symbols in International Tables for Crystallography (2006). Vol. A, ch. 12.1, pp. 818-820
{{Crystal systems Symmetry Crystallography Discrete groups