Convex metric space

In mathematics, convex metric spaces are, intuitively, metric spaces with the property any "segment" joining two points in that space has other points in it besides the endpoints.

Formally, consider a metric space (''X'', ''d'') and let ''x'' and ''y'' be two points in ''X''. A point ''z'' in ''X'' is said to be ''between'' ''x'' and ''y'' if all three points are distinct, and

: $d(x, z)+d(z, y)=d(x, y),\,$

that is, the triangle inequality becomes an equality. A convex metric space is a metric space (''X'', ''d'') such that, for any two distinct points ''x'' and ''y'' in ''X'', there exists a third point ''z'' in ''X'' lying between ''x'' and ''y''.

Metric convexity:
* does not imply convexity in the usual sense for subsets of Euclidean space (see the example of the rational numbers)
* nor does it imply path-connectedness (see the example of the rational numbers)
* nor does it imply geodesic convexity for Riemannian manifolds (consider, for example, the Euclidean plane with a closed disc removed).

Examples

* Euclidean spaces, that is, the usual three-dimensional space and its analogues for other dimensions, are convex metric spaces. Given any two distinct points $x$ and $y$ in such a space, the set of all points $z$ satisfying the above "triangle equality" forms the line segment between $x$ and $y,$ which always has other points except $x$ and $y,$ in fact, it has a continuum of points.

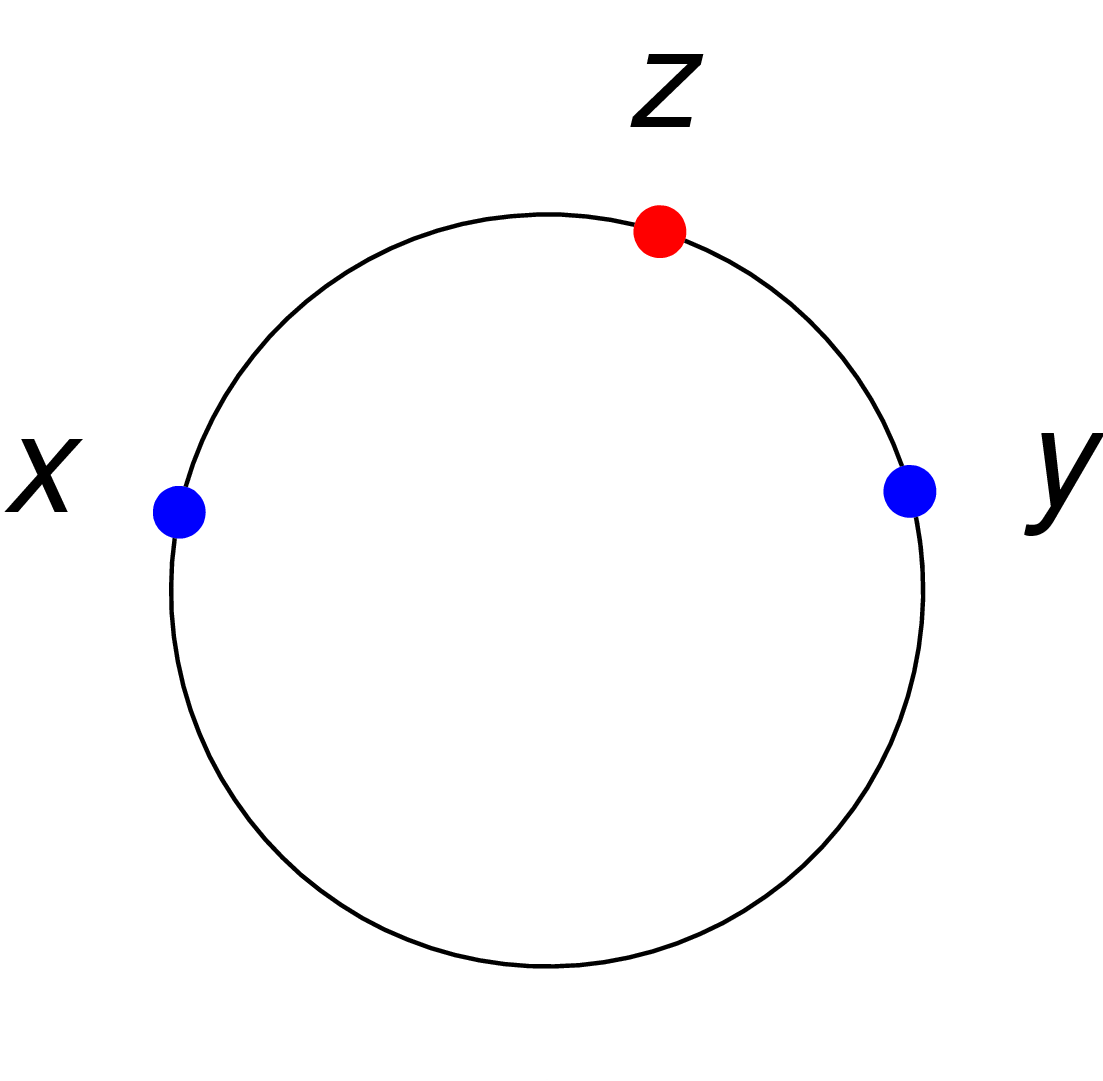* Any convex set in a Euclidean space is a convex metric space with the induced Euclidean norm. For closed sets the converse is also true: if a closed subset of a Euclidean space together with the induced distance is a convex metric space, then it is a convex set (this is a particular case of a more general statement to be discussed below).
* A circle is a convex metric space, if the distance between two points is defined as the length of the shortest arc on the circle connecting them.

Metric segments

Let $(X, d)$ be a metric space (which is not necessarily convex). A subset $S$ of $X$ is called a metric segment between two distinct points $x$ and $z$ in $X,$ if there exists a closed interval , c/math> on the real line and an isometry

: \gamma: , c\to X,\,

such that \gamma( , c=S, $\gamma(a)=x$ and $\gamma(c)=z.$

Any point ''y'' in a metric segment $S$, except its endpoints $x$ and $z$, is between $x$ and $z$. ''Proof'': since ''y'' is on ''S'', which is the image of ,c there must be some point b in ,csuch that $\gamma(b)=y$. By the properties of an isometry, $d(x,y) = b-a$ and $d(y,z) = c-b$. Therefore, $d(x,y)+d(y,z) = c-a$, which equals $d(x,z)$ by the properties of an isometry.

As such, if a metric space $(X, d)$ admits metric segments between any two distinct points in the space, then it is a convex metric space.

The converse is not true, in general. The rational numbers form a convex metric space with the usual distance, yet there exists no segment connecting two rational numbers which is made up of rational numbers only. If however, $(X, d)$ is a convex metric space, and, in addition, it is complete, one can prove that for any two points $x\ne y$ in $X$ there exists a metric segment connecting them (which is not necessarily unique).

Convex metric spaces and convex sets

As mentioned in the examples section, closed subsets of Euclidean spaces are convex metric spaces if and only if they are convex sets. It is then natural to think of convex metric spaces as generalizing the notion of convexity beyond Euclidean spaces, with usual linear segments replaced by metric segments.

It is important to note, however, that metric convexity defined this way does not have one of the most important properties of Euclidean convex sets, that being that the intersection of two convex sets is convex. Indeed, as mentioned in the examples section, a circle, with the distance between two points measured along the shortest arc connecting them, is a ( complete) convex metric space. Yet, if $x$ and $y$ are two points on a circle diametrically opposite to each other, there exist two metric segments connecting them (the two arcs into which these points split the circle), and those two arcs are metrically convex, but their intersection is the set $\$ which is not metrically convex.

See also

*Intrinsic metric

References

*

*

{{Convex analysis and variational analysis

Convex geometry
Metric geometry