Conical surface

In geometry, a conical surface is an unbounded surface in three-dimensional space formed from the union of infinite lines that pass through a fixed point and a space curve.

Definitions

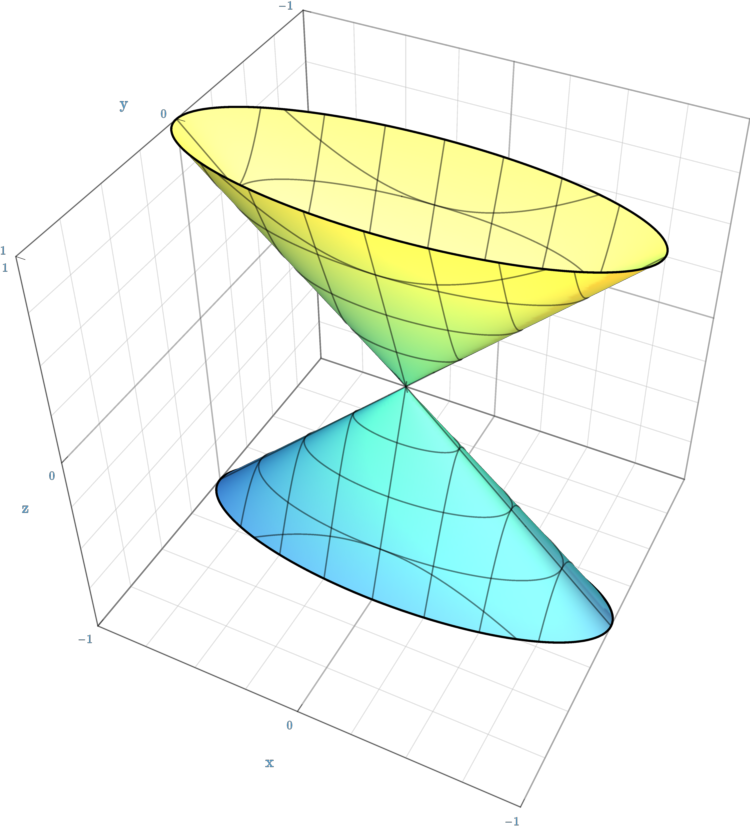
A (''general'') conical surface is the unbounded surface formed by the union of all the straight lines that pass through a fixed point — the ''apex'' or ''vertex'' — and any point of some fixed space curve — the ''directrix'' — that does not contain the apex. Each of those lines is called a ''generatrix'' of the surface. The directrix is often taken as a plane curve, in a plane not containing the apex, but this is not a requirement.

In general, a conical surface consists of two congruent unbounded halves joined by the apex. Each half is called a nappe, and is the union of all the rays that start at the apex and pass through a point of some fixed space curve. Sometimes the term "conical surface" is used to mean just one nappe.

Special cases

If the directrix is a circle $C$, and the apex is located on the circle's ''axis'' (the line that contains the center of $C$ and is perpendicular to its plane), one obtains the ''right circular conical surface'' or double cone. More generally, when the directrix $C$ is an ellipse, or any conic section, and the apex is an arbitrary point not on the plane of $C$, one obtains an elliptic cone.

Equations

A conical surface $S$ can be described parametrically as
:$S(t,u) = v + u q(t)$,
where $v$ is the apex and $q$ is the directrix.

Related surface

Conical surfaces are ruled surfaces, surfaces that have a straight line through each of their points. Patches of conical surfaces that avoid the apex are special cases of developable surfaces, surfaces that can be unfolded to a flat plane without stretching. When the directrix has the property that the angle it subtends from the apex is exactly $2\pi$, then each nappe of the conical surface, including the apex, is a developable surface.

A cylindrical surface can be viewed as a limiting case of a conical surface whose apex is moved off to infinity in a particular direction. Indeed, in projective geometry a cylindrical surface is just a special case of a conical surface.

See also

*Conic section
* Quadric

References

{{DEFAULTSORT:Conical Surface
Euclidean solid geometry
Surfaces