Chandy–Misra–Haas Algorithm Resource Model on:
[Wikipedia]
[Google]
[Amazon]
The Chandy–Misra–Haas algorithm resource model checks for
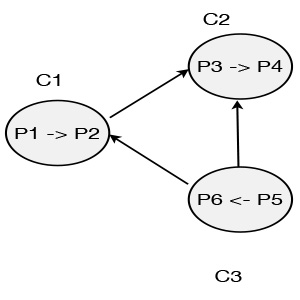 ''P''''1'' initiates deadlock detection. ''C''''1'' sends the probe saying ''P''''2'' depends on ''P''''3''. Once the message is received by ''C''''2'', it checks whether ''P''''3'' is idle. ''P''''3'' is idle because it is locally dependent on ''P''''4'' and updates ''dependent''''3''(2) to True.
As above, ''C''''2'' sends probe to ''C''''3'' and ''C''''3'' sends probe to ''C''''1''. At ''C''''1'', ''P''''1'' is idle so it update ''dependent''''1''(1) to True. Therefore, deadlock can be declared.
''P''''1'' initiates deadlock detection. ''C''''1'' sends the probe saying ''P''''2'' depends on ''P''''3''. Once the message is received by ''C''''2'', it checks whether ''P''''3'' is idle. ''P''''3'' is idle because it is locally dependent on ''P''''4'' and updates ''dependent''''3''(2) to True.
As above, ''C''''2'' sends probe to ''C''''3'' and ''C''''3'' sends probe to ''C''''1''. At ''C''''1'', ''P''''1'' is idle so it update ''dependent''''1''(1) to True. Therefore, deadlock can be declared.
deadlock
Deadlock commonly refers to:
* Deadlock (computer science), a situation where two processes are each waiting for the other to finish
* Deadlock (locksmithing) or deadbolt, a physical door locking mechanism
* Political deadlock or gridlock, a si ...
in a distributed system
Distributed computing is a field of computer science that studies distributed systems, defined as computer systems whose inter-communicating components are located on different networked computers.
The components of a distributed system commun ...
. It was developed by K. Mani Chandy
Kanianthra Mani Chandy (born 25 October 1944) is the Simon Ramo Professor of Computer Science at the California Institute of Technology (Caltech). He has been the Executive Officer of the Computer Science Department twice, and he has been a pr ...
, Jayadev Misra
Jayadev Misra is an Indian-born computer scientist who has spent most of his professional career in the United States. He is the Schlumberger Centennial Chair Emeritus in computer science and a University Distinguished Teaching Professor Emeritus ...
and Laura M. Haas
Laura M. Haas is an American computer scientist noted for her research in database systems and
information integration. She is best known for creating systems and tools for the integration of heterogeneous data from diverse sources, including fe ...
.
Locally dependent
Consider the n processes ''P''''1'', ''P''''2'', ''P''''3'', ''P''''4'', ''P''''5,'', ... ,''P''''n'' which are performed in a single system (controller). ''P''''1'' is locally dependent on ''P''''n'', if ''P''''1'' depends on ''P''''2'', ''P''''2'' on ''P''''3,'' so on and ''P''''n−1'' on ''P''''n''. That is, if , then is locally dependent on . If ''P''''1'' is said to be locally dependent to itself if it is locally dependent on ''P''''n'' and ''P''''n'' depends on ''P''''1'': i.e. if , then is locally dependent on itself.Description
Thealgorithm
In mathematics and computer science, an algorithm () is a finite sequence of Rigour#Mathematics, mathematically rigorous instructions, typically used to solve a class of specific Computational problem, problems or to perform a computation. Algo ...
uses a message called probe(i,j,k) to transfer a message from controller of process ''P''''j'' to controller of process ''P''''k''. It specifies a message started by process ''P''''i'' to find whether a deadlock has occurred or not. Every process ''P''''j'' maintains a boolean array ''dependent'' which contains the information about the processes that depend on it. Initially the values of each array are all "false".
Controller sending a probe
Before sending, the probe checks whether ''P''''j'' is locally dependent on itself. If so, a deadlock occurs. Otherwise it checks whether ''P''''j'', and ''P''''k'' are in different controllers, are locally dependent and ''P''''j'' is waiting for the resource that is locked by ''P''''k''. Once all the conditions are satisfied it sends the probe.Controller receiving a probe
On the receiving side, the controller checks whether ''P''''k'' is performing a task. If so, it neglects the probe. Otherwise, it checks the responses given ''P''''k'' to ''P''''j'' and ''dependent''''k''(i) is false. Once it is verified, it assigns true to ''dependent''''k''(i). Then it checks whether k is equal to i. If both are equal, a deadlock occurs, otherwise it sends the probe to next dependent process.Algorithm
Inpseudocode
In computer science, pseudocode is a description of the steps in an algorithm using a mix of conventions of programming languages (like assignment operator, conditional operator, loop) with informal, usually self-explanatory, notation of actio ...
, the algorithm works as follows:
Controller sending a probe
if ''P''''j'' is locally dependent on itself then declare deadlock else for all ''P''''j'',''P''''k'' such that (i) ''P''''i'' is locally dependent on ''P''''j'', (ii) ''P''''j'' is waiting for P''''k'' and (iii) ''P''''j'', ''P''''k'' are on different controllers. send probe(i, j, k). to home site of ''P''''k''Controller receiving a probe
if (i)''P''''k'' is idle / blocked (ii) ''dependent''''k''(i) = false, and (iii) ''P''''k'' has not replied to all requests of to ''P''''j'' then begin "dependents""k"(i) = true; if k i then declare that ''P''''i'' is deadlocked else for all ''P''''a'',''P''''b'' such that (i) ''P''''k'' is locally dependent on ''P''''a'', (ii) ''P''''a'' is waiting for P''''b'' and (iii) ''P''''a'', ''P''''b'' are on different controllers. send probe(i, a, b). to home site of ''P''''b'' endExample
 ''P''''1'' initiates deadlock detection. ''C''''1'' sends the probe saying ''P''''2'' depends on ''P''''3''. Once the message is received by ''C''''2'', it checks whether ''P''''3'' is idle. ''P''''3'' is idle because it is locally dependent on ''P''''4'' and updates ''dependent''''3''(2) to True.
As above, ''C''''2'' sends probe to ''C''''3'' and ''C''''3'' sends probe to ''C''''1''. At ''C''''1'', ''P''''1'' is idle so it update ''dependent''''1''(1) to True. Therefore, deadlock can be declared.
''P''''1'' initiates deadlock detection. ''C''''1'' sends the probe saying ''P''''2'' depends on ''P''''3''. Once the message is received by ''C''''2'', it checks whether ''P''''3'' is idle. ''P''''3'' is idle because it is locally dependent on ''P''''4'' and updates ''dependent''''3''(2) to True.
As above, ''C''''2'' sends probe to ''C''''3'' and ''C''''3'' sends probe to ''C''''1''. At ''C''''1'', ''P''''1'' is idle so it update ''dependent''''1''(1) to True. Therefore, deadlock can be declared.
Complexity
Suppose there are controllers and processes, at most messages need to be exchanged to detect a deadlock, with a delay of messages.References
{{DEFAULTSORT:Chandy-Misra-Haas algorithm resource model Algorithms