Centripetal Catmull–Rom Spline on:
[Wikipedia]
[Google]
[Amazon]
In 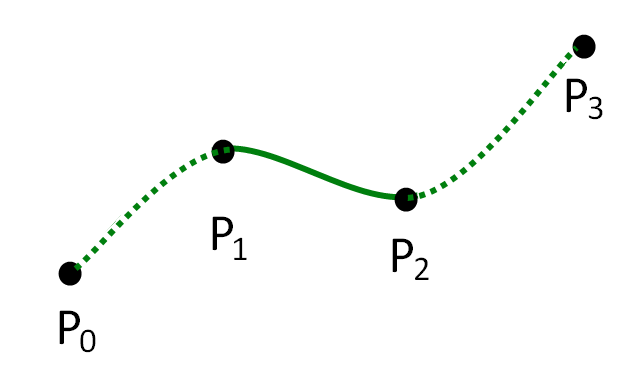

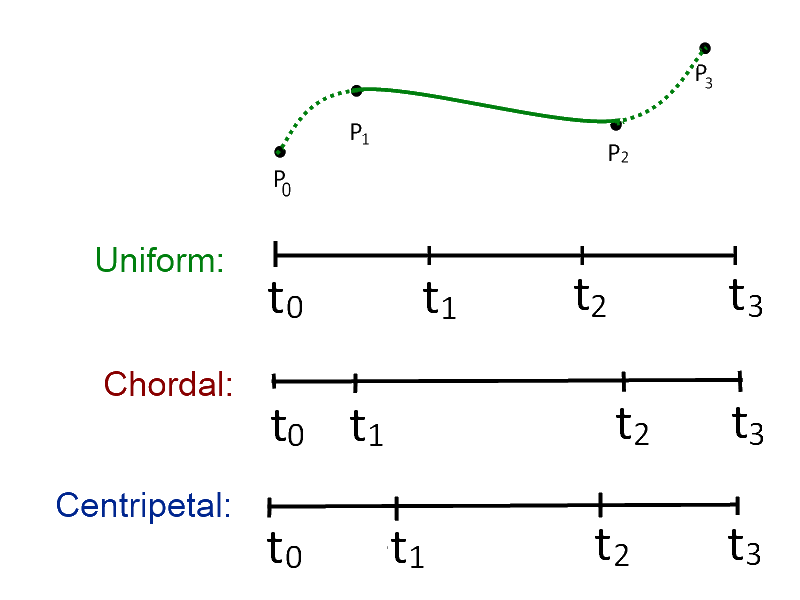 Let denote a point. For a curve segment defined by points and knot sequence , the centripetal Catmull–Rom spline can be produced by:
:
where
:
:
:
:
:
and
:
in which ranges from 0 to 1 for knot parameterization, and with . For centripetal Catmull–Rom spline, the value of is . When , the resulting curve is the standard uniform Catmull–Rom spline; when , the result is a chordal Catmull–Rom spline.
Plugging into the spline equations and shows that the value of the spline curve at is . Similarly, substituting into the spline equations shows that at . This is true independent of the value of since the equation for is not needed to calculate the value of at points and .
Let denote a point. For a curve segment defined by points and knot sequence , the centripetal Catmull–Rom spline can be produced by:
:
where
:
:
:
:
:
and
:
in which ranges from 0 to 1 for knot parameterization, and with . For centripetal Catmull–Rom spline, the value of is . When , the resulting curve is the standard uniform Catmull–Rom spline; when , the result is a chordal Catmull–Rom spline.
Plugging into the spline equations and shows that the value of the spline curve at is . Similarly, substituting into the spline equations shows that at . This is true independent of the value of since the equation for is not needed to calculate the value of at points and .
 The extension to 3D points is simply achieved by considering a generic 3D point and
:
The extension to 3D points is simply achieved by considering a generic 3D point and
:
import numpy
import matplotlib.pyplot as plt
QUADRUPLE_SIZE: int = 4
def num_segments(point_chain: tuple) -> int:
# There is 1 segment per 4 points, so we must subtract 3 from the number of points
return len(point_chain) - (QUADRUPLE_SIZE - 1)
def flatten(list_of_lists) -> list:
# E.g. mapping 1, 2
using UnityEngine;
// a single catmull-rom curve
public struct CatmullRomCurve
using UnityEngine;
// Draws a catmull-rom spline in the scene view,
// along the child objects of the transform of this component
public class CatmullRomSpline : MonoBehaviour
float GetT( float t, float alpha, const FVector& p0, const FVector& p1 )
FVector CatmullRom( const FVector& p0, const FVector& p1, const FVector& p2, const FVector& p3, float t /* between 0 and 1 */, float alpha=.5f /* between 0 and 1 */ )
Catmull-Rom curve with no cusps and no self-intersections
implementation in Java
Catmull-Rom curve with no cusps and no self-intersections
simplified implementation in C++
Catmull-Rom splines
interactive generation via Python, in a Jupyter notebook {{DEFAULTSORT:Centripetal Catmull-Rom spline Splines (mathematics) Articles with example C Sharp code Articles with example Python (programming language) code
computer graphics
Computer graphics deals with generating images with the aid of computers. Today, computer graphics is a core technology in digital photography, film, video games, cell phone and computer displays, and many specialized applications. A great deal ...
, the centripetal Catmull–Rom spline is a variant form of the Catmull–Rom spline
In numerical analysis, a cubic Hermite spline or cubic Hermite interpolator is a spline where each piece is a third-degree polynomial specified in Hermite form, that is, by its values and first derivatives at the end points of the corresponding ...
, originally formulated by Edwin Catmull and Raphael Rom
Raphael "Raphi" Rom is an Israeli computer scientist working at Technion – Israel Institute of Technology.
Rom earned his Ph.D. in 1975 from the University of Utah, under the supervision of Thomas Stockham. He is known for his contribution to th ...
, which can be evaluated using a recursive algorithm proposed by Barry and Goldman. It is a type of interpolating spline (a curve that goes through its control points) defined by four control points , with the curve drawn only from to .

Definition

 Let denote a point. For a curve segment defined by points and knot sequence , the centripetal Catmull–Rom spline can be produced by:
:
where
:
:
:
:
:
and
:
in which ranges from 0 to 1 for knot parameterization, and with . For centripetal Catmull–Rom spline, the value of is . When , the resulting curve is the standard uniform Catmull–Rom spline; when , the result is a chordal Catmull–Rom spline.
Plugging into the spline equations and shows that the value of the spline curve at is . Similarly, substituting into the spline equations shows that at . This is true independent of the value of since the equation for is not needed to calculate the value of at points and .
Let denote a point. For a curve segment defined by points and knot sequence , the centripetal Catmull–Rom spline can be produced by:
:
where
:
:
:
:
:
and
:
in which ranges from 0 to 1 for knot parameterization, and with . For centripetal Catmull–Rom spline, the value of is . When , the resulting curve is the standard uniform Catmull–Rom spline; when , the result is a chordal Catmull–Rom spline.
Plugging into the spline equations and shows that the value of the spline curve at is . Similarly, substituting into the spline equations shows that at . This is true independent of the value of since the equation for is not needed to calculate the value of at points and .
 The extension to 3D points is simply achieved by considering a generic 3D point and
:
The extension to 3D points is simply achieved by considering a generic 3D point and
:
Advantages
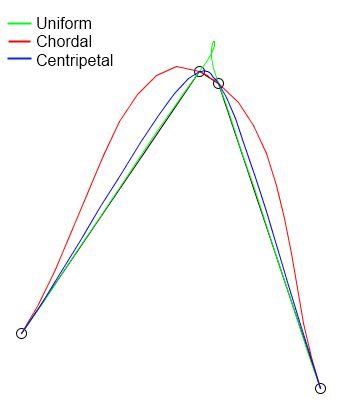
Centripetal Catmull–Rom spline has several desirable mathematical properties compared to the original and the other types of Catmull-Rom formulation. First, it will not form loop or self-intersection within a curve segment. Second, cusp will never occur within a curve segment. Third, it follows the control points more tightly.
Other uses
Incomputer vision
Computer vision is an Interdisciplinarity, interdisciplinary scientific field that deals with how computers can gain high-level understanding from digital images or videos. From the perspective of engineering, it seeks to understand and automate t ...
, centripetal Catmull-Rom spline has been used to formulate an active model for segmentation. The method is termed active spline model. The model is devised on the basis of active shape model, but uses centripetal Catmull-Rom spline to join two successive points (active shape model uses simple straight line), so that the total number of points necessary to depict a shape is less. The use of centripetal Catmull-Rom spline makes the training of a shape model much simpler, and it enables a better way to edit a contour after segmentation.
Code example in Python
The following is an implementation of the Catmull–Rom spline in Python that produces the plot shown beneath., 5
The comma is a punctuation mark that appears in several variants in different languages. It has the same shape as an apostrophe or single closing quotation mark () in many typefaces, but it differs from them in being placed on the baseline ...
to , 2, 3, 4, 5
The comma is a punctuation mark that appears in several variants in different languages. It has the same shape as an apostrophe or single closing quotation mark () in many typefaces, but it differs from them in being placed on the baseline o ...
return lem for lst in list_of_lists for elem in lst
Lem may refer to:
Places
* 3836 Lem, an asteroid named after Stanisław Lem
* , a municipality in Jutland
People Given name or nickname
(Alphabetical by surname)
* Lemuel Lem Barney (born 1945), American football player
* Lem Billings (1916� ...
def catmull_rom_spline(
P0: tuple,
P1: tuple,
P2: tuple,
P3: tuple,
num_points: int,
alpha: float = 0.5,
):
"""
Compute the points in the spline segment
:param P0, P1, P2, and P3: The (x,y) point pairs that define the Catmull-Rom spline
:param num_points: The number of points to include in the resulting curve segment
:param alpha: 0.5 for the centripetal spline, 0.0 for the uniform spline, 1.0 for the chordal spline.
:return: The points
"""
# Calculate t0 to t4. Then only calculate points between P1 and P2.
# Reshape linspace so that we can multiply by the points P0 to P3
# and get a point for each value of t.
def tj(ti: float, pi: tuple, pj: tuple) -> float:
xi, yi = pi
xj, yj = pj
dx, dy = xj - xi, yj - yi
l = (dx ** 2 + dy ** 2) ** 0.5
return ti + l ** alpha
t0: float = 0.0
t1: float = tj(t0, P0, P1)
t2: float = tj(t1, P1, P2)
t3: float = tj(t2, P2, P3)
t = numpy.linspace(t1, t2, num_points).reshape(num_points, 1)
A1 = (t1 - t) / (t1 - t0) * P0 + (t - t0) / (t1 - t0) * P1
A2 = (t2 - t) / (t2 - t1) * P1 + (t - t1) / (t2 - t1) * P2
A3 = (t3 - t) / (t3 - t2) * P2 + (t - t2) / (t3 - t2) * P3
B1 = (t2 - t) / (t2 - t0) * A1 + (t - t0) / (t2 - t0) * A2
B2 = (t3 - t) / (t3 - t1) * A2 + (t - t1) / (t3 - t1) * A3
points = (t2 - t) / (t2 - t1) * B1 + (t - t1) / (t2 - t1) * B2
return points
def catmull_rom_chain(points: tuple, num_points: int) -> list:
"""
Calculate Catmull-Rom for a sequence of initial points and return the combined curve.
:param points: Base points from which the quadruples for the algorithm are taken
:param num_points: The number of points to include in each curve segment
:return: The chain of all points (points of all segments)
"""
point_quadruples = ( # Prepare function inputs
(pointsdx_segment_start + d
DX may refer to:
In arts and entertainment
* ''DX'' (album), a 2013 album by Friendzone
* D-Generation X, a professional wrestling stable
* Design Exchange, a museum of design in Toronto
* '' Deus Ex'', a series of video games
** ''Deus Ex'' ...
for d in range(QUADRUPLE_SIZE))
for idx_segment_start in range(num_segments(points))
)
all_splines = (catmull_rom_spline(*pq, num_points) for pq in point_quadruples)
return flatten(all_splines)
if __name__ "__main__":
POINTS: tuple = ((0, 1.5), (2, 2), (3, 1), (4, 0.5), (5, 1), (6, 2), (7, 3)) # Red points
NUM_POINTS: int = 100 # Density of blue chain points between two red points
chain_points: list = catmull_rom_chain(POINTS, NUM_POINTS)
assert len(chain_points) num_segments(POINTS) * NUM_POINTS # 400 blue points for this example
plt.plot(*zip(*chain_points), c="blue")
plt.plot(*zip(*POINTS), c="red", linestyle="none", marker="o")
plt.show()
Code example in Unity C#
Code example in Unreal C++
See also
* Cubic Hermite splinesReferences
External links
Catmull-Rom curve with no cusps and no self-intersections
implementation in Java
Catmull-Rom curve with no cusps and no self-intersections
simplified implementation in C++
Catmull-Rom splines
interactive generation via Python, in a Jupyter notebook {{DEFAULTSORT:Centripetal Catmull-Rom spline Splines (mathematics) Articles with example C Sharp code Articles with example Python (programming language) code