Causal Diagram on:
[Wikipedia]
[Google]
[Amazon]
 In the philosophy of science, a causal model (or structural causal model) is a
In the philosophy of science, a causal model (or structural causal model) is a
 In the philosophy of science, a causal model (or structural causal model) is a
In the philosophy of science, a causal model (or structural causal model) is a conceptual model
A conceptual model is a representation of a system. It consists of concepts used to help people knowledge, know, understanding, understand, or simulation, simulate a subject the model represents. In contrast, physical models are physical object su ...
that describes the causal mechanisms of a system
A system is a group of Interaction, interacting or interrelated elements that act according to a set of rules to form a unified whole. A system, surrounded and influenced by its environment (systems), environment, is described by its boundaries, ...
. Causal models can improve study designs by providing clear rules for deciding which independent variables need to be included/controlled for.
They can allow some questions to be answered from existing observational data without the need for an interventional study such as a randomized controlled trial. Some interventional studies are inappropriate for ethical or practical reasons, meaning that without a causal model, some hypotheses cannot be tested.
Causal models can help with the question of ''external validity'' (whether results from one study apply to unstudied populations). Causal models can allow data from multiple studies to be merged (in certain circumstances) to answer questions that cannot be answered by any individual data set.
Causal models have found applications in signal processing, epidemiology and machine learning.
Definition
Judea Pearl defines a causal model as an ordered triple , where U is a set of exogenous variables whose values are determined by factors outside the model; V is a set of endogenous variables whose values are determined by factors within the model; and E is a set ofstructural equation
Structural equation modeling (SEM) is a label for a diverse set of methods used by scientists in both experimental and observational research across the sciences, business, and other fields. It is used most in the social and behavioral scienc ...
s that express the value of each endogenous variable as a function of the values of the other variables in U and V.
History
Aristotle defined a taxonomy of causality, including material, formal, efficient and final causes. Hume rejected Aristotle's taxonomy in favor ofcounterfactuals
Counterfactual conditionals (also ''subjunctive'' or ''X-marked'') are conditional sentences which discuss what would have been true under different circumstances, e.g. "If Peter believed in ghosts, he would be afraid to be here." Counterfactual ...
. At one point, he denied that objects have "powers" that make one a cause and another an effect. Later he adopted "if the first object had not been, the second had never existed" (" but-for" causation).
In the late 19th century, the discipline of statistics began to form. After a years-long effort to identify causal rules for domains such as biological inheritance, Galton introduced the concept of mean regression (epitomized by the sophomore slump in sports) which later led him to the non-causal concept of correlation
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics ...
.
As a positivist, Pearson expunged the notion of causality from much of science as an unprovable special case of association and introduced the correlation coefficient as the metric of association. He wrote, "Force as a cause of motion is exactly the same as a tree god as a cause of growth" and that causation was only a "fetish among the inscrutable arcana of modern science". Pearson founded ''Biometrika
''Biometrika'' is a peer-reviewed scientific journal published by Oxford University Press for thBiometrika Trust The editor-in-chief is Paul Fearnhead (Lancaster University). The principal focus of this journal is theoretical statistics. It was es ...
'' and the Biometrics Lab at University College London, which became the world leader in statistics.
In 1908 Hardy
Hardy may refer to:
People
* Hardy (surname)
* Hardy (given name)
* Hardy (singer), American singer-songwriter Places Antarctica
* Mount Hardy, Enderby Land
* Hardy Cove, Greenwich Island
* Hardy Rocks, Biscoe Islands
Australia
* Hardy, Sout ...
and Weinberg solved the problem of trait stability that had led Galton to abandon causality, by resurrecting Mendelian inheritance.
In 1921 Wright's path analysis became the theoretical ancestor of causal modeling and causal graphs. He developed this approach while attempting to untangle the relative impacts of heredity
Heredity, also called inheritance or biological inheritance, is the passing on of traits from parents to their offspring; either through asexual reproduction or sexual reproduction, the offspring cells or organisms acquire the genetic inform ...
, development and environment on guinea pig coat patterns. He backed up his then-heretical claims by showing how such analyses could explain the relationship between guinea pig birth weight, '' in utero'' time and litter size. Opposition to these ideas by prominent statisticians led them to be ignored for the following 40 years (except among animal breeders). Instead scientists relied on correlations, partly at the behest of Wright's critic (and leading statistician), Fisher. One exception was Burks, a student who in 1926 was the first to apply path diagrams to represent a mediating influence (''mediator'') and to assert that holding a mediator constant induces errors. She may have invented path diagrams independently.
In 1923, Neyman Neyman is a surname. Notable people with the surname include:
* Abraham Neyman (born 1949), Israeli mathematician
*Benny Neyman (1951–2008), Dutch singer
* Jerzy Neyman (1894–1981), Polish mathematician; Neyman construction and Neyman–Pearson ...
introduced the concept of a potential outcome, but his paper was not translated from Polish to English until 1990.
In 1958 Cox warned that controlling for a variable Z is valid only if it is highly unlikely to be affected by independent variables.
In the 1960s, Duncan
Duncan may refer to:
People
* Duncan (given name), various people
* Duncan (surname), various people
* Clan Duncan
* Justice Duncan (disambiguation)
Places
* Duncan Creek (disambiguation)
* Duncan River (disambiguation)
* Duncan Lake (d ...
, Blalock, Goldberger Goldberger is a surname of Jewish origin. Notable people with the surname include:
Science
*Arthur Goldberger (1930–2009), economist
*Joseph Goldberger (1874–1929), physician
*Marvin Leonard Goldberger (1922–2014), physicist
Sports
*Andre ...
and others rediscovered path analysis. While reading Blalock's work on path diagrams, Duncan remembered a lecture by Ogburn twenty years earlier that mentioned a paper by Wright that in turn mentioned Burks.
Sociologists originally called causal models structural equation modeling
Structural equation modeling (SEM) is a label for a diverse set of methods used by scientists in both experimental and observational research across the sciences, business, and other fields. It is used most in the social and behavioral scienc ...
, but once it became a rote method, it lost its utility, leading some practitioners to reject any relationship to causality. Economists adopted the algebraic part of path analysis, calling it simultaneous equation modeling. However, economists still avoided attributing causal meaning to their equations.
Sixty years after his first paper, Wright published a piece that recapitulated it, following Karlin et al.'s critique, which objected that it handled only linear relationships and that robust, model-free presentations of data were more revealing.
In 1973 Lewis advocated replacing correlation with but-for causality (counterfactuals). He referred to humans' ability to envision alternative worlds in which a cause did or not occur, and in which an effect appeared only following its cause. In 1974 Rubin introduced the notion of "potential outcomes" as a language for asking causal questions.
In 1983 Cartwright
Cartwright may refer to:
* Wainwright (occupation), a tradesperson skilled in the making and repairing of carts or wagons
* Cartwright (surname), including the list of people
Places
; Australia
* Cartwright, New South Wales
; Canada
* Cartwr ...
proposed that any factor that is "causally relevant" to an effect be conditioned on, moving beyond simple probability as the only guide.
In 1986 Baron and Kenny introduced principles for detecting and evaluating mediation in a system of linear equations. As of 2014 their paper was the 33rd most-cited of all time. That year Greenland and Robins introduced the "exchangeability" approach to handling confounding by considering a counterfactual. They proposed assessing what would have happened to the treatment group if they had not received the treatment and comparing that outcome to that of the control group. If they matched, confounding was said to be absent.Ladder of causation
Pearl's causal metamodel involves a three-level abstraction he calls the ladder of causation. The lowest level, Association (seeing/observing), entails the sensing of regularities or patterns in the input data, expressed as correlations. The middle level, Intervention (doing), predicts the effects of deliberate actions, expressed as causal relationships. The highest level,Counterfactuals
Counterfactual conditionals (also ''subjunctive'' or ''X-marked'') are conditional sentences which discuss what would have been true under different circumstances, e.g. "If Peter believed in ghosts, he would be afraid to be here." Counterfactual ...
(imagining), involves constructing a theory of (part of) the world that explains why specific actions have specific effects and what happens in the absence of such actions.
Association
One object is associated with another if observing one changes the probability of observing the other. Example: shoppers who buy toothpaste are more likely to also buy dental floss. Mathematically: : or the probability of (purchasing) floss given (the purchase of) toothpaste. Associations can also be measured via computing thecorrelation
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics ...
of the two events. Associations have no causal implications. One event could cause the other, the reverse could be true, or both events could be caused by some third event (unhappy hygienist shames shopper into treating their mouth better ).
Intervention
This level asserts specific causal relationships between events. Causality is assessed by experimentally performing some action that affects one of the events. Example: if we doubled the price of toothpaste, what would be the new probability of purchasing? Causality cannot be established by examining history (of price changes) because the price change may have been for some other reason that could itself affect the second event (a tariff that increases the price of both goods). Mathematically: : where ''do'' is an operator that signals the experimental intervention (doubling the price). The operator indicates performing the minimal change in the world necessary to create the intended effect, a "mini-surgery" on the model with as little change from reality as possible.Counterfactuals
The highest level, counterfactual, involves consideration of an alternate version of a past event, or what would happen under different circumstances for the same experimental unit. For example, what is the probability that, if a store had doubled the price of floss, the toothpaste-purchasing shopper would still have bought it? : Counterfactuals can indicate the existence of a causal relationship. Models that can answer counterfactuals allow precise interventions whose consequences can be predicted. At the extreme, such models are accepted as physical laws (as in the laws of physics, e.g., inertia, which says that if force is not applied to a stationary object, it will not move).Causality
Causality vs correlation
Statistics revolves around the analysis of relationships among multiple variables. Traditionally, these relationships are described as correlations, associations without any implied causal relationships. Causal models attempt to extend this framework by adding the notion of causal relationships, in which changes in one variable cause changes in others. Twentieth century definitions ofcausality
Causality (also referred to as causation, or cause and effect) is influence by which one event, process, state, or object (''a'' ''cause'') contributes to the production of another event, process, state, or object (an ''effect'') where the cau ...
relied purely on probabilities/associations. One event () was said to cause another if it raises the probability of the other (). Mathematically this is expressed as:
:.
Such definitions are inadequate because other relationships (e.g., a common cause for and ) can satisfy the condition. Causality is relevant to the second ladder step. Associations are on the first step and provide only evidence to the latter.
A later definition attempted to address this ambiguity by conditioning on background factors. Mathematically:
:,
where is the set of background variables and represents the values of those variables in a specific context. However, the required set of background variables is indeterminate (multiple sets may increase the probability), as long as probability is the only criterion.
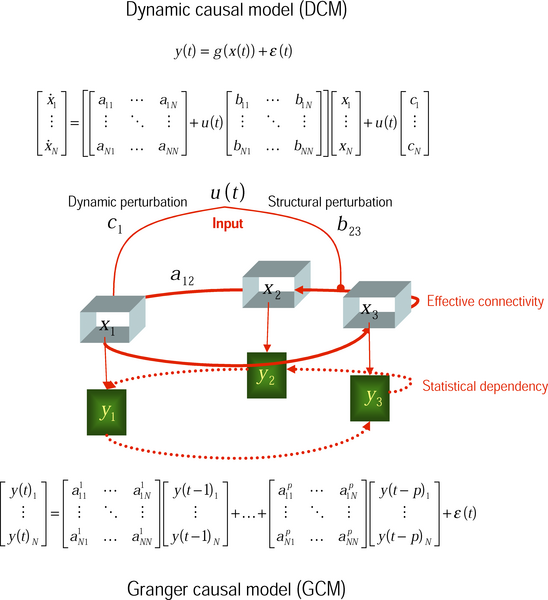
Other attempts to define causality include Granger causality, a statistical hypothesis test
A statistical hypothesis test is a method of statistical inference used to decide whether the data at hand sufficiently support a particular hypothesis.
Hypothesis testing allows us to make probabilistic statements about population parameters.
...
that causality
Causality (also referred to as causation, or cause and effect) is influence by which one event, process, state, or object (''a'' ''cause'') contributes to the production of another event, process, state, or object (an ''effect'') where the cau ...
(in economics) can be assessed by measuring the ability to predict the future values of one time series using prior values of another time series.
Types
A cause can be necessary, sufficient, contributory or some combination.Necessary
For ''x'' to be a necessary cause of ''y'', the presence of ''y'' must imply the prior occurrence of ''x''. The presence of ''x'', however, does not imply that ''y'' will occur. Necessary causes are also known as "but-for" causes, as in ''y'' would not have occurred but for the occurrence of ''x''.Sufficient causes
For ''x'' to be a sufficient cause of ''y'', the presence of ''x'' must imply the subsequent occurrence of ''y''. However, another cause ''z'' may independently cause ''y''. Thus the presence of ''y'' does not require the prior occurrence of ''x''.Contributory causes
For ''x'' to be a contributory cause of ''y'', the presence of ''x'' must increase the likelihood of ''y''. If the likelihood is 100%, then ''x'' is instead called sufficient. A contributory cause may also be necessary.Model
Causal diagram
A causal diagram is a directed graph that displays causal relationships between variables in a causal model. A causal diagram includes a set of variables (ornodes
In general, a node is a localized swelling (a "knot") or a point of intersection (a Vertex (graph theory), vertex).
Node may refer to:
In mathematics
*Vertex (graph theory), a vertex in a mathematical graph
*Vertex (geometry), a point where two ...
). Each node is connected by an arrow to one or more other nodes upon which it has a causal influence. An arrowhead delineates the direction of causality, e.g., an arrow connecting variables and with the arrowhead at indicates that a change in causes a change in (with an associated probability). A ''path'' is a traversal of the graph between two nodes following causal arrows.
Causal diagrams include causal loop diagrams, directed acyclic graphs, and Ishikawa diagrams.
Causal diagrams are independent of the quantitative probabilities that inform them. Changes to those probabilities (e.g., due to technological improvements) do not require changes to the model.
Model elements
Causal models have formal structures with elements with specific properties.Junction patterns
The three types of connections of three nodes are linear chains, branching forks and merging colliders.= Chain
= Chains are straight line connections with arrows pointing from cause to effect. In this model, is a mediator in that it mediates the change that would otherwise have on . := Fork
= In forks, one cause has multiple effects. The two effects have a common cause. There exists a (non-causal)spurious correlation
In statistics, a spurious relationship or spurious correlation is a mathematical relationship in which two or more events or variables are associated but '' not'' causally related, due to either coincidence or the presence of a certain third, uns ...
between and that can be eliminated by conditioning on (for a specific value of ).
:
"Conditioning on " means "given " (i.e., given a value of ).
An elaboration of a fork is the confounder:
:
In such models, is a common cause of and (which also causes ), making the confounder.
= Collider
= In colliders, multiple causes affect one outcome. Conditioning on (for a specific value of ) often reveals a non-causal negative correlation between and . This negative correlation has been called collider bias and the "explain-away" effect as explains away the correlation between and . The correlation can be positive in the case where contributions from both and are necessary to affect . :Node types
= Mediator
= A mediator node modifies the effect of other causes on an outcome (as opposed to simply affecting the outcome). For example, in the chain example above, is a mediator, because it modifies the effect of (an indirect cause of ) on (the outcome).= Confounder
= A confounder node affects multiple outcomes, creating a positive correlation among them.Instrumental variable
An ''instrumental variable'' is one that: * has a path to the outcome; * has no other path to causal variables; * has no direct influence on the outcome. Regression coefficients can serve as estimates of the causal effect of an instrumental variable on an outcome as long as that effect is not confounded. In this way, instrumental variables allow causal factors to be quantified without data on confounders. For example, given the model: : is an instrumental variable, because it has a path to the outcome and is unconfounded, e.g., by . In the above example, if and take binary values, then the assumption that does not occur is called ''monotonicity''. Refinements to the technique include creating an instrument by conditioning on other variable to block the paths between the instrument and the confounder and combining multiple variables to form a single instrument.Mendelian randomization
Definition: Mendelian randomization uses measured variation in genes of known function to examine the causal effect of a modifiable exposure on disease in observational studies. Because genes vary randomly across populations, presence of a gene typically qualifies as an instrumental variable, implying that in many cases, causality can be quantified using regression on an observational study.Associations
Independence conditions
Independence conditions are rules for deciding whether two variables are independent of each other. Variables are independent if the values of one do not directly affect the values of the other. Multiple causal models can share independence conditions. For example, the models : and : have the same independence conditions, because conditioning on leaves and independent. However, the two models do not have the same meaning and can be falsified based on data (that is, if observational data show an association between and after conditioning on , then both models are incorrect). Conversely, data cannot show which of these two models are correct, because they have the same independence conditions. Conditioning on a variable is a mechanism for conducting hypothetical experiments. Conditioning on a variable involves analyzing the values of other variables for a given value of the conditioned variable. In the first example, conditioning on implies that observations for a given value of should show no dependence between and . If such a dependence exists, then the model is incorrect. Non-causal models cannot make such distinctions, because they do not make causal assertions.Confounder/deconfounder
An essential element of correlational study design is to identify potentially confounding influences on the variable under study, such as demographics. These variables are controlled for to eliminate those influences. However, the correct list of confounding variables cannot be determined ''a priori''. It is thus possible that a study may control for irrelevant variables or even (indirectly) the variable under study. Causal models offer a robust technique for identifying appropriate confounding variables. Formally, Z is a confounder if "Y is associated with Z via paths not going through X". These can often be determined using data collected for other studies. Mathematically, if : then we say that X and Y are confounded (by some confounder variable Z). Earlier, allegedly incorrect definitions of confounder include: * "Any variable that is correlated with both X and Y." * Y is associated with Z among the unexposed. * Noncollapsibility: A difference between the "crude relative risk and the relative risk resulting after adjustment for the potential confounder". * Epidemiological: A variable associated with X in the population at large and associated with Y among people unexposed to X. The latter is flawed in that given that in the model: : Z matches the definition, but is a mediator, not a confounder, and is an example of controlling for the outcome. In the model : Traditionally, B was considered to be a confounder, because it is associated with X and with Y but is not on a causal path nor is it a descendant of anything on a causal path. Controlling for B causes it to become a confounder. This is known as M-bias.Backdoor adjustment
For analysing the causal effect of X on Y in a causal model we need to adjust for all confounder variables (deconfounding). To identify the set of confounders we need to (1) block every noncausal path between X and Y by this set (2) without disrupting any causal paths and (3) without creating any spurious paths. Definition: a backdoor path from variable X to Y is any path from X to Y that starts with an arrow pointing to X. Definition: Given an ordered pair of variables (X,Y) in a model, a set of confounder variables Z satisfies the backdoor criterion if (1) no confounder variable Z is a descendent of X and (2) all backdoor paths between X and Y are blocked by the set of confounders. If the backdoor criterion is satisfied for (X,Y), X and Y are deconfounded by the set of confounder variables. It is not necessary to control for any variables other than the confounders. The backdoor criterion is a sufficient but not necessary condition to find a set of variables Z to decounfound the analysis of the causal effect of X on y. When the causal model is a plausible representation of reality and the backdoor criterion is satisfied, then partial regression coefficients can be used as (causal) path coefficients (for linear relationships). :Frontdoor adjustment
If the elements of a blocking path are all unobservable, the backdoor path is not calculable, but if all forward paths from have elements where there are no open paths , then we can use , the set of all s, to measure . Effectively, there are conditions where can act as a proxy for . Definition: a frontdoor path is a direct causal path for which data is available for all , intercepts all directed paths to , there are no unblocked paths from to , and all backdoor paths from to are blocked by . The following converts a do expression into a do-free expression by conditioning on the variables along the front-door path. :