Cauchy–Riemann equations on:
[Wikipedia]
[Google]
[Amazon]
 In the field of
In the field of
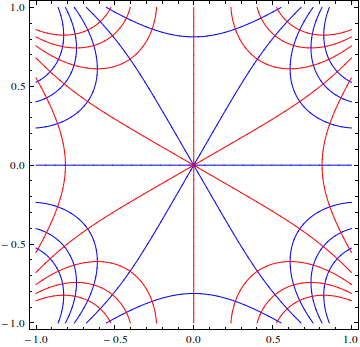 A standard physical interpretation of the Cauchy–Riemann equations going back to Riemann's work on function theory is that ''u'' represents a
A standard physical interpretation of the Cauchy–Riemann equations going back to Riemann's work on function theory is that ''u'' represents a
Cauchy–Riemann Equations Module by John H. Mathews
{{DEFAULTSORT:Cauchy-Riemann equations Eponymous equations of mathematics Partial differential equations Complex analysis Harmonic functions Bernhard Riemann Augustin-Louis Cauchy
complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebraic ...
in mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, the Cauchy–Riemann equations, named after Augustin Cauchy
Baron Augustin-Louis Cauchy ( , , ; ; 21 August 1789 – 23 May 1857) was a French mathematician, engineer, and physicist. He was one of the first to rigorously state and prove the key theorems of calculus (thereby creating real a ...
and Bernhard Riemann
Georg Friedrich Bernhard Riemann (; ; 17September 182620July 1866) was a German mathematician who made profound contributions to analysis, number theory, and differential geometry. In the field of real analysis, he is mostly known for the f ...
, consist of a system
A system is a group of interacting or interrelated elements that act according to a set of rules to form a unified whole. A system, surrounded and influenced by its open system (systems theory), environment, is described by its boundaries, str ...
of two partial differential equation
In mathematics, a partial differential equation (PDE) is an equation which involves a multivariable function and one or more of its partial derivatives.
The function is often thought of as an "unknown" that solves the equation, similar to ho ...
s which form a necessary and sufficient condition for a complex function
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebraic g ...
of a complex variable to be complex differentiable
In mathematics, a holomorphic function is a complex-valued function of one or Function of several complex variables, more complex number, complex variables that is Differentiable function#Differentiability in complex analysis, complex differ ...
.
These equations are
and
where and are real bivariate differentiable functions.
Typically, and are respectively the real and imaginary part
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form ...
s of a complex
Complex commonly refers to:
* Complexity, the behaviour of a system whose components interact in multiple ways so possible interactions are difficult to describe
** Complex system, a system composed of many components which may interact with each ...
-valued function of a single complex variable where and are real variables; and are real differentiable function
In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non- vertical tangent line at each interior point in ...
s of the real variables. Then is complex differentiable
In mathematics, a holomorphic function is a complex-valued function of one or Function of several complex variables, more complex number, complex variables that is Differentiable function#Differentiability in complex analysis, complex differ ...
at a complex point if and only if the partial derivatives of and satisfy the Cauchy–Riemann equations at that point.
A holomorphic function
In mathematics, a holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighbourhood of each point in a domain in complex coordinate space . The existence of a complex de ...
is a complex function that is differentiable at every point of some open subset of the complex plane . It has been proved that holomorphic functions are analytic and analytic complex functions are complex-differentiable. In particular, holomorphic functions are infinitely complex-differentiable.
This equivalence between differentiability and analyticity is the starting point of all complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebraic ...
.
History
The Cauchy–Riemann equations first appeared in the work ofJean le Rond d'Alembert
Jean-Baptiste le Rond d'Alembert ( ; ; 16 November 1717 – 29 October 1783) was a French mathematician, mechanician, physicist, philosopher, and music theorist. Until 1759 he was, together with Denis Diderot, a co-editor of the ''Encyclopé ...
. Later, Leonhard Euler
Leonhard Euler ( ; ; ; 15 April 170718 September 1783) was a Swiss polymath who was active as a mathematician, physicist, astronomer, logician, geographer, and engineer. He founded the studies of graph theory and topology and made influential ...
connected this system to the analytic functions
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions. Functions of each type are infinitely differentiable, but complex ...
. Cauchy then used these equations to construct his theory of functions. Riemann's dissertation on the theory of functions appeared in 1851.
Simple example
Suppose that . The complex-valued function is differentiable at any point in the complex plane. The real part and the imaginary part are and their partial derivatives are We see that indeed the Cauchy–Riemann equations are satisfied, and .Interpretation and reformulation
The Cauchy-Riemann equations are one way of looking at the condition for a function to be differentiable in the sense ofcomplex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebraic ...
: in other words, they encapsulate the notion of function of a complex variable by means of conventional differential calculus
In mathematics, differential calculus is a subfield of calculus that studies the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus—the study of the area beneath a curve. ...
. In the theory there are several other major ways of looking at this notion, and the translation of the condition into other language is often needed.
Conformal mappings
First, the Cauchy–Riemann equations may be written in complex form In this form, the equations correspond structurally to the condition that theJacobian matrix
In vector calculus, the Jacobian matrix (, ) of a vector-valued function of several variables is the matrix of all its first-order partial derivatives. If this matrix is square, that is, if the number of variables equals the number of component ...
is of the form
where and . A matrix of this form is the matrix representation of a complex number. Geometrically, such a matrix is always the composition
Composition or Compositions may refer to:
Arts and literature
*Composition (dance), practice and teaching of choreography
* Composition (language), in literature and rhetoric, producing a work in spoken tradition and written discourse, to include ...
of a rotation
Rotation or rotational/rotary motion is the circular movement of an object around a central line, known as an ''axis of rotation''. A plane figure can rotate in either a clockwise or counterclockwise sense around a perpendicular axis intersect ...
with a scaling, and in particular preserves angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two R ...
s. The Jacobian of a function takes infinitesimal line segments at the intersection of two curves in and rotates them to the corresponding segments in . Consequently, a function satisfying the Cauchy–Riemann equations, with a nonzero derivative, preserves the angle between curves in the plane. That is, the Cauchy–Riemann equations are the conditions for a function to be conformal.
Moreover, because the composition of a conformal transformation with another conformal transformation is also conformal, the composition of a solution of the Cauchy–Riemann equations with a conformal map must itself solve the Cauchy–Riemann equations. Thus the Cauchy–Riemann equations are conformally invariant.
Complex differentiability
Let where and are real-valued functions, be a complex-valued function of a complex variable where and are real variables. so the function can also be regarded as a function of real variables and . Then, the ''complex-derivative'' of at a point is defined by provided this limit exists (that is, the limit exists along every path approaching , and does not depend on the chosen path). A fundamental result ofcomplex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebraic ...
is that is complex differentiable
In mathematics, a holomorphic function is a complex-valued function of one or Function of several complex variables, more complex number, complex variables that is Differentiable function#Differentiability in complex analysis, complex differ ...
at (that is, it has a complex-derivative), if and only if
In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The biconditional is true in two cases, where either bo ...
the bivariate real function
In mathematical analysis, and applications in geometry, applied mathematics, engineering, and natural sciences, a function of a real variable is a function whose domain is the real numbers \mathbb, or a subset of \mathbb that contains an inter ...
s and are differentiable
In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non- vertical tangent line at each interior point in ...
at and satisfy the Cauchy–Riemann equations at this point.
In fact, if the complex derivative exists at , then it may be computed by taking the limit at along the real axis and the imaginary axis, and the two limits must be equal. Along the real axis, the limit is
and along the imaginary axis, the limit is
So, the equality of the derivatives implies
which is the complex form of Cauchy–Riemann equations () at .
(Note that if is complex differentiable at , it is also real differentiable and the Jacobian of at is the complex scalar , regarded as a real-linear map of , since the limit as .)
Conversely, if is differentiable at (in the real sense) and satisfies the Cauchy-Riemann equations there, then it is complex-differentiable at this point. Assume that as a function of two real variables and is differentiable at (real differentiable). This is equivalent to the existence of the following linear approximation where , , , and as .
Since and , the above can be re-written as
Now, if is real, , while if it is imaginary, then . Therefore, the second term is independent of the path of the limit when (and only when) it vanishes identically: , which is precisely the Cauchy–Riemann equations in the complex form. This proof also shows that, in that case,
Note that the hypothesis of real differentiability at the point is essential and cannot be dispensed with. For example, the function , regarded as a complex function with imaginary part identically zero, has both partial derivatives at , and it moreover satisfies the Cauchy–Riemann equations at that point, but it is not differentiable in the sense of real functions (of several variables), and so the first condition, that of real differentiability, is not met. Therefore, this function is not complex differentiable.
Some sources state a sufficient condition for the complex differentiability at a point as, in addition to the Cauchy–Riemann equations, the partial derivatives of and be continuous at the point because this continuity condition ensures the existence of the aforementioned linear approximation. Note that it is not a necessary condition for the complex differentiability. For example, the function is complex differentiable at 0, but its real and imaginary parts have discontinuous partial derivatives there. Since complex differentiability is usually considered in an open set, where it in fact implies continuity of all partial derivatives (see below), this distinction is often elided in the literature.
Independence of the complex conjugate
The above proof suggests another interpretation of the Cauchy–Riemann equations. Thecomplex conjugate
In mathematics, the complex conjugate of a complex number is the number with an equal real part and an imaginary part equal in magnitude but opposite in sign. That is, if a and b are real numbers, then the complex conjugate of a + bi is a - ...
of , denoted , is defined by
for real variables '''' and . Defining the two Wirtinger derivatives as
the Cauchy–Riemann equations can then be written as a single equation
and the complex derivative of '''' in that case is In this form, the Cauchy–Riemann equations can be interpreted as the statement that a complex function '''' of a complex variable '''' is independent of the variable . As such, we can view analytic functions as true functions of ''one'' complex variable ('''') instead of complex functions of ''two'' real variables ('''' and '''').
Physical interpretation
 A standard physical interpretation of the Cauchy–Riemann equations going back to Riemann's work on function theory is that ''u'' represents a
A standard physical interpretation of the Cauchy–Riemann equations going back to Riemann's work on function theory is that ''u'' represents a velocity potential
A velocity potential is a scalar potential used in potential flow theory. It was introduced by Joseph-Louis Lagrange in 1788.
It is used in continuum mechanics, when a continuum occupies a simply-connected region and is irrotational. In such a ca ...
of an incompressible steady fluid flow in the plane, and ''v'' is its stream function
In fluid dynamics, two types of stream function (or streamfunction) are defined:
* The two-dimensional (or Lagrange) stream function, introduced by Joseph Louis Lagrange in 1781, is defined for incompressible flow, incompressible (divergence-free ...
. Suppose that the pair of (twice continuously differentiable
In mathematics, a differentiable function of one Real number, real variable is a Function (mathematics), function whose derivative exists at each point in its Domain of a function, domain. In other words, the Graph of a function, graph of a differ ...
) functions ''u'' and ''v'' satisfies the Cauchy–Riemann equations. We will take ''u'' to be a velocity potential, meaning that we imagine a flow of fluid in the plane such that the velocity vector of the fluid at each point of the plane is equal to the gradient
In vector calculus, the gradient of a scalar-valued differentiable function f of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p gives the direction and the rate of fastest increase. The g ...
of ''u'', defined by
By differentiating the Cauchy–Riemann equations for the functions ''u'' and ''v'', with the symmetry of second derivatives, one shows that ''u'' solves Laplace's equation
In mathematics and physics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace, who first studied its properties in 1786. This is often written as
\nabla^2\! f = 0 or \Delta f = 0,
where \Delt ...
:
That is, ''u'' is a harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f\colon U \to \mathbb R, where is an open subset of that satisfies Laplace's equation, that i ...
. This means that the divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the rate that the vector field alters the volume in an infinitesimal neighborhood of each point. (In 2D this "volume" refers to ...
of the gradient is zero, and so the fluid is incompressible.
The function ''v'' also satisfies the Laplace equation, by a similar analysis. Also, the Cauchy–Riemann equations imply that the dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. N ...
(), i.e., the direction of the maximum slope of ''u'' and that of ''v'' are orthogonal to each other. This implies that the gradient of ''u'' must point along the curves; so these are the streamlines of the flow. The curves are the equipotential curve
A contour line (also isoline, isopleth, isoquant or isarithm) of a Function of several real variables, function of two variables is a curve along which the function has a constant value, so that the curve joins points of equal value. It is a ...
s of the flow.
A holomorphic function can therefore be visualized by plotting the two families of level curves and . Near points where the gradient of ''u'' (or, equivalently, ''v'') is not zero, these families form an orthogonal
In mathematics, orthogonality (mathematics), orthogonality is the generalization of the geometric notion of ''perpendicularity''. Although many authors use the two terms ''perpendicular'' and ''orthogonal'' interchangeably, the term ''perpendic ...
family of curves. At the points where , the stationary points of the flow, the equipotential curves of intersect. The streamlines also intersect at the same point, bisecting the angles formed by the equipotential curves.
Harmonic vector field
Another interpretation of the Cauchy–Riemann equations can be found in Pólya & Szegő. Suppose that ''u'' and ''v'' satisfy the Cauchy–Riemann equations in an open subset of R2, and consider thevector field
In vector calculus and physics, a vector field is an assignment of a vector to each point in a space, most commonly Euclidean space \mathbb^n. A vector field on a plane can be visualized as a collection of arrows with given magnitudes and dire ...
regarded as a (real) two-component vector. Then the second Cauchy–Riemann equation () asserts that is irrotational
In vector calculus, a conservative vector field is a vector field that is the gradient of some function. A conservative vector field has the property that its line integral is path independent; the choice of path between two points does not chan ...
(its curl is 0):
The first Cauchy–Riemann equation () asserts that the vector field is solenoidal (or divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the rate that the vector field alters the volume in an infinitesimal neighborhood of each point. (In 2D this "volume" refers to ...
-free):
Owing respectively to Green's theorem
In vector calculus, Green's theorem relates a line integral around a simple closed curve to a double integral over the plane region (surface in \R^2) bounded by . It is the two-dimensional special case of Stokes' theorem (surface in \R^3) ...
and the divergence theorem
In vector calculus, the divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, reprinted in is a theorem relating the '' flux'' of a vector field through a closed surface to the ''divergence'' of the field in the volume ...
, such a field is necessarily a conservative
Conservatism is a cultural, social, and political philosophy and ideology that seeks to promote and preserve traditional institutions, customs, and values. The central tenets of conservatism may vary in relation to the culture and civiliza ...
one, and it is free from sources or sinks, having net flux equal to zero through any open domain without holes. (These two observations combine as real and imaginary parts in Cauchy's integral theorem.) In fluid dynamics
In physics, physical chemistry and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids – liquids and gases. It has several subdisciplines, including (the study of air and other gases in motion ...
, such a vector field is a potential flow
In fluid dynamics, potential flow or irrotational flow refers to a description of a fluid flow with no vorticity in it. Such a description typically arises in the limit of vanishing viscosity, i.e., for an inviscid fluid and with no vorticity pre ...
. In magnetostatics
Magnetostatics is the study of magnetic fields in systems where the electric currents, currents are steady current, steady (not changing with time). It is the magnetic analogue of electrostatics, where the electric charge, charges are stationary ...
, such vector fields model static magnetic field
A magnetic field (sometimes called B-field) is a physical field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular ...
s on a region of the plane containing no current. In electrostatics
Electrostatics is a branch of physics that studies slow-moving or stationary electric charges.
Since classical antiquity, classical times, it has been known that some materials, such as amber, attract lightweight particles after triboelectric e ...
, they model static electric fields in a region of the plane containing no electric charge.
This interpretation can equivalently be restated in the language of differential form
In mathematics, differential forms provide a unified approach to define integrands over curves, surfaces, solids, and higher-dimensional manifolds. The modern notion of differential forms was pioneered by Élie Cartan. It has many applications ...
s. The pair ''u'' and ''v'' satisfy the Cauchy–Riemann equations if and only if the one-form is both closed and coclosed (a harmonic differential form).
Preservation of complex structure
Another formulation of the Cauchy–Riemann equations involves the complex structure in the plane, given by This is a complex structure in the sense that the square of ''J'' is the negative of the 2×2 identity matrix: . As above, if ''u''(''x'',''y'') and ''v''(''x'',''y'') are two functions in the plane, put TheJacobian matrix
In vector calculus, the Jacobian matrix (, ) of a vector-valued function of several variables is the matrix of all its first-order partial derivatives. If this matrix is square, that is, if the number of variables equals the number of component ...
of ''f'' is the matrix of partial derivatives
Then the pair of functions ''u'', ''v'' satisfies the Cauchy–Riemann equations if and only if the 2×2 matrix ''Df'' commutes with ''J''.
This interpretation is useful in symplectic geometry
Symplectic geometry is a branch of differential geometry and differential topology that studies symplectic manifolds; that is, differentiable manifolds equipped with a closed, nondegenerate 2-form. Symplectic geometry has its origins in the ...
, where it is the starting point for the study of pseudoholomorphic curves.
Other representations
Other representations of the Cauchy–Riemann equations occasionally arise in othercoordinate system
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine and standardize the position of the points or other geometric elements on a manifold such as Euclidean space. The coordinates are ...
s. If () and () hold for a differentiable pair of functions ''u'' and ''v'', then so do
for any coordinate system such that the pair is orthonormal and positively oriented. As a consequence, in particular, in the system of coordinates given by the polar representation , the equations then take the form
Combining these into one equation for gives
The inhomogeneous Cauchy–Riemann equations consist of the two equations for a pair of unknown functions and of two real variables
for some given functions and defined in an open subset of R2. These equations are usually combined into a single equation
where ''f'' = ''u'' + i''v'' and ''𝜑'' = (''α'' + i''β'')/2.
If ''𝜑'' is ''C''''k'', then the inhomogeneous equation is explicitly solvable in any bounded domain ''D'', provided ''𝜑'' is continuous on the closure of ''D''. Indeed, by the Cauchy integral formula,
for all ''ζ'' ∈ ''D''.
Generalizations
Goursat's theorem and its generalizations
Suppose that is a complex-valued function which isdifferentiable
In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non- vertical tangent line at each interior point in ...
as a function . Then Goursat's theorem asserts that ''f'' is analytic in an open complex domain Ω if and only if it satisfies the Cauchy–Riemann equation in the domain. In particular, continuous differentiability of ''f'' need not be assumed.
The hypotheses of Goursat's theorem can be weakened significantly. If is continuous in an open set Ω and the partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant (as opposed to the total derivative, in which all variables are allowed to vary). P ...
s of ''f'' with respect to ''x'' and ''y'' exist in Ω, and satisfy the Cauchy–Riemann equations throughout Ω, then ''f'' is holomorphic (and thus analytic). This result is the Looman–Menchoff theorem.
The hypothesis that ''f'' obey the Cauchy–Riemann equations throughout the domain Ω is essential. It is possible to construct a continuous function satisfying the Cauchy–Riemann equations at a point, but which is not analytic at the point (e.g., . Similarly, some additional assumption is needed besides the Cauchy–Riemann equations (such as continuity), as the following example illustrates
which satisfies the Cauchy–Riemann equations everywhere, but fails to be continuous at ''z'' = 0.
Nevertheless, if a function satisfies the Cauchy–Riemann equations in an open set in a weak sense, then the function is analytic. More precisely:
: If is locally integrable in an open domain and satisfies the Cauchy–Riemann equations weakly, then agrees almost everywhere
In measure theory (a branch of mathematical analysis), a property holds almost everywhere if, in a technical sense, the set for which the property holds takes up nearly all possibilities. The notion of "almost everywhere" is a companion notion to ...
with an analytic function in .
This is in fact a special case of a more general result on the regularity of solutions of hypoelliptic partial differential equations.
Several variables
There are Cauchy–Riemann equations, appropriately generalized, in the theory ofseveral complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functions defined on the complex coordinate space \mathbb C^n, that is, -tuples of complex numbers. The name of the field dealing with the properties ...
. They form a significant overdetermined system of PDEs. This is done using a straightforward generalization of the Wirtinger derivative
In complex analysis of one and several complex variables, Wirtinger derivatives (sometimes also called Wirtinger operators), named after Wilhelm Wirtinger who introduced them in 1927 in the course of his studies on the theory of functions of se ...
, where the function in question is required to have the (partial) Wirtinger derivative with respect to each complex variable vanish.
Complex differential forms
As often formulated, the ''d-bar operator'' annihilates holomorphic functions. This generalizes most directly the formulation whereBäcklund transform
Viewed as conjugate harmonic functions, the Cauchy–Riemann equations are a simple example of a Bäcklund transform. More complicated, generally non-linear Bäcklund transforms, such as in the sine-Gordon equation, are of great interest in the theory ofsoliton
In mathematics and physics, a soliton is a nonlinear, self-reinforcing, localized wave packet that is , in that it preserves its shape while propagating freely, at constant velocity, and recovers it even after collisions with other such local ...
s and integrable systems.
Definition in Clifford algebra
In theClifford algebra
In mathematics, a Clifford algebra is an algebra generated by a vector space with a quadratic form, and is a unital associative algebra with the additional structure of a distinguished subspace. As -algebras, they generalize the real number ...
, the complex number is represented as where , (, so ). The Dirac operator
In mathematics and in quantum mechanics, a Dirac operator is a first-order differential operator that is a formal square root, or half-iterate, of a second-order differential operator such as a Laplacian. It was introduced in 1847 by William Ham ...
in this Clifford algebra is defined as . The function is considered analytic if and only if , which can be calculated in the following way:
Grouping by and :
Hence, in traditional notation:
Conformal mappings in higher dimensions
Let Ω be an open set in the Euclidean space . The equation for an orientation-preserving mapping to be a conformal mapping (that is, angle-preserving) is that where ''Df'' is the Jacobian matrix, with transpose , and ''I'' denotes the identity matrix. For , this system is equivalent to the standard Cauchy–Riemann equations of complex variables, and the solutions are holomorphic functions. In dimension , this is still sometimes called the Cauchy–Riemann system, and Liouville's theorem implies, under suitable smoothness assumptions, that any such mapping is aMöbius transformation
In geometry and complex analysis, a Möbius transformation of the complex plane is a rational function of the form
f(z) = \frac
of one complex number, complex variable ; here the coefficients , , , are complex numbers satisfying .
Geometrically ...
.
Lie pseudogroups
One might seek to generalize the Cauchy-Riemann equations instead by asking more generally when are the solutions of a system of PDEs closed under composition. The theory of Lie Pseudogroups addresses these kinds of questions.See also
* List of complex analysis topics *Cauchy integral theorem
In mathematics, the Cauchy integral theorem (also known as the Cauchy–Goursat theorem) in complex analysis, named after Augustin-Louis Cauchy (and Édouard Goursat), is an important statement about line integrals for holomorphic functions in t ...
* Morera's theorem
* Wirtinger derivatives
References
Sources
* * * *Further reading
* * *External links
*Cauchy–Riemann Equations Module by John H. Mathews
{{DEFAULTSORT:Cauchy-Riemann equations Eponymous equations of mathematics Partial differential equations Complex analysis Harmonic functions Bernhard Riemann Augustin-Louis Cauchy