Cauchy–Frobenius Lemma

Burnside's lemma, sometimes also called Burnside's counting theorem, the Cauchy–Frobenius lemma, or the orbit-counting theorem, is a result in group theory that is often useful in taking account of symmetry when counting mathematical objects. It was discovered by Augustin Louis Cauchy and Ferdinand Georg Frobenius, and became well known after William Burnside quoted it. The result enumerates orbits of a symmetry group acting on some objects: that is, it counts distinct objects, considering objects symmetric to each other as the same; or counting distinct objects up to a symmetry equivalence relation; or counting only objects in canonical form. For example, in describing possible organic compounds of certain type, one considers them up to spatial rotation symmetry: different rotated drawings of a given molecule are chemically identical. (However a mirror reflection might give a different compound.)

Formally, let $G$ be a finite group that acts on a set $X$. For each $g$ in $G$, let $X^g$ denote the set of elements in $X$ that are fixed by $g$ (left invariant by $g$): that is, $X^g = \.$ Burnside's lemma asserts the following formula for the number of orbits, denoted $, X/G,$:

$, X/G, = \frac\sum_, X^g, .$

Thus the number of orbits (a natural number or +∞) is equal to the average number of points fixed by an element of ''G''. For an infinite group $G$, there is still a bijection:

$G \times X/G \ \longleftrightarrow\ \coprod_ X^g .$

Examples of applications to enumeration

Necklaces

There are 8 possible bit strings of length 3, but tying together the string ends gives only four distinct 2-colored necklaces of length 3, given by the canonical forms 000, 001, 011, 111: the other strings 100 and 010 are equivalent to 001 by rotation, while 110 and 101 are equivalent to 011. That is, rotation equivalence splits the set $X$ of strings into four orbits: $X = \\cup \\cup \\cup \.$The Burnside formula uses the number of rotations, which is 3 including the null rotation, and the number of bit strings left unchanged by each rotation. All 8 bit vectors are unchanged by the null rotation, and two (000 and 111) are unchanged by the other two rotations. Thus the number of orbits is:
$4 = \frac(8+2+2).$

For length 4, there are 16 possible bit strings; 4 rotations; the null rotation leaves all 16 strings unchanged; the 1-rotation and 3-rotation each leave two strings unchanged (0000 and 1111); the 2-rotation leaves 4 bit strings unchanged (0000, 0101, 1010, 1111). The number of distinct necklaces is thus: $6 = \tfrac(16+2+4+2)$, represented by the canonical forms 0000, 0001, 0011, 0101, 0111, 1111.

The general case of ''n'' bits and ''k'' colors is given by a necklace polynomial.

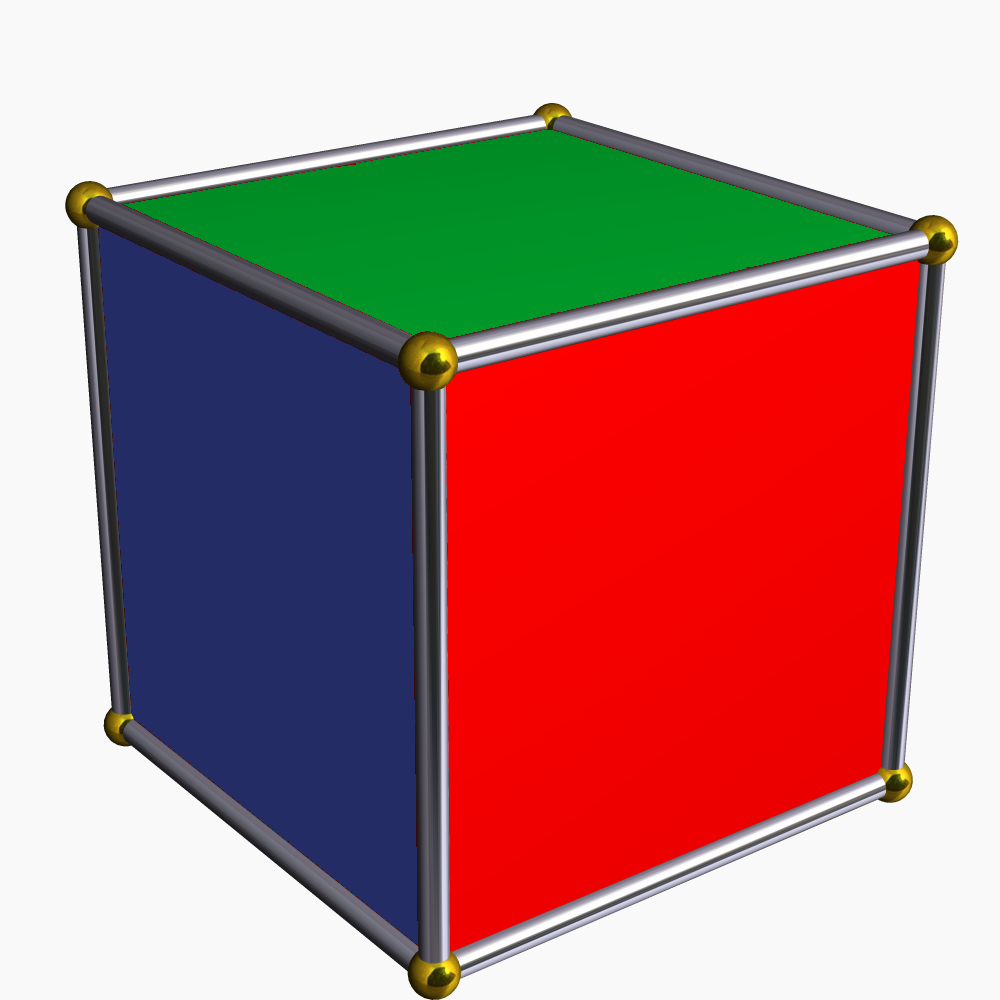
Colorings of a cube

Burnside's lemma can compute the number of rotationally distinct colourings of the faces of a cube using three colours.

Let $X$ be the set of 3⁶ possible face color combinations that can be applied to a fixed cube, and let the rotation group ''G'' of the cube act on $X$ by moving the colored faces: two colorings in $X$ belong to the same orbit precisely when one is a rotation of the other. Rotationally distinct colorings correspond to group orbits, and can be found by counting the sizes of the fixed sets for the 24 elements of ''G'', the colorings left unchanged by each rotation:

* the identity element fixes all 3⁶ colorings
* six 90-degree face rotations each fix 3³ colorings
* three 180-degree face rotations each fix 3⁴ colorings
* eight 120-degree vertex rotations each fix 3² colorings
* six 180-degree edge rotations each fix 3³ colorings.

A detailed examination may be found
here.

The average fixed-set size is thus:

: $, X/G, = \frac\left(3^6+6\cdot 3^3 + 3 \cdot 3^4 + 8 \cdot 3^2 + 6 \cdot 3^3 \right) = 57.$

There are 57 rotationally distinct colourings of the faces of a cube in three colours. In general, the number of rotationally distinct colorings of the faces of a cube in ''n'' colors is:

: $\frac\left(n^6+3n^4 + 12n^3 + 8n^2\right).$

Proof

In the proof of Burnside's lemma, the first step is to re-express the sum over the group elements ''g'' ∈ ''G'' as an equivalent sum over the set of elements ''x'' ∈ ''X'':

:$\sum_, X^g, = \#\ = \sum_ , G_x, .$

Here $X^g = \$ is the set of points of $X$ fixed by the element $g$ of $G$, whereas $G_x = \$ is the stabilizer subgroup of $G$, consisting of those symmetries that fix the point $x \in X$.)

The orbit-stabilizer theorem says that for each $x \in X$ there is a natural bijection between the orbit $G \cdot x = \$ and the set of left cosets $G / G_x$. Lagrange's theorem implies that

, G \cdot x, = : G_x= , G, / , G_x, .

The sum may therefore be rewritten as

$\sum_ , G_x, = \sum_ \frac = , G, \sum_\frac.$

Writing $X$ as the disjoint union of its orbits in $X/G$ gives

$, G, \sum_\frac = , G, \sum_ \sum_ \frac = , G, \sum_ 1 = , G, \cdot, X/G, .$

Putting everything together gives the desired result:

$\sum_, X^g, = , G, \cdot , X/G, .$

This is similar to the proof of the conjugacy class equation, which considers the conjugation action of $G$ on itself, that is, it is the case $X = G$ and $g \cdot x = gxg^$, so that the stabilizer of $x$ is the centralizer $G_x = Z_G(x)$.

Enumeration vs. generation

Burnside's lemma counts distinct objects, but it does not construct them. In general, combinatorial generation with isomorph rejection considers the symmetries of $g$ on objects $x$. But instead of checking that $g \cdot x = x$, it checks that $g \cdot x$ has not already been generated. One way to accomplish this is by checking that $g \cdot x$ is not lexicographically less than $x$, using the lexicographically least member of each equivalence class as the canonical form of the class. Counting the objects generated with such a technique can verify that Burnside's lemma was correctly applied.

History: the lemma that is not Burnside's

William Burnside stated and proved this lemma in his 1897 book on finite groups, attributing it to . But even prior to Frobenius, the formula was known to Cauchy in 1845. Consequently, this lemma is sometimes referred to as the lemma that is not Burnside's.. Misnaming scientific discoveries is referred to as Stigler's law of eponymy.

See also

* Pólya enumeration theorem
* Cycle index

Notes

References

* Also availabl
here
at Archive.org. (This is the first edition; the introduction to the second edition contains Burnside's famous ''volte face'' regarding the utility of representation theory.)
* .
* .
* {{citation , last=Rotman , first=Joseph , title=An introduction to the theory of groups , publisher=Springer-Verlag , year=1995 , isbn=0-387-94285-8.

Lemmas in group theory