Capillary Length

The capillary length or capillary constant, is a length scaling factor that relates gravity and surface tension. It is a fundamental physical property that governs the behavior of menisci, and is found when body forces (gravity) and surface forces (Laplace pressure) are in equilibrium.

The pressure of a static fluid does not depend on the shape, total mass or surface area of the fluid. It is directly proportional to the fluid's specific weight – the force exerted by gravity over a specific volume, and its vertical height. However, a fluid also experiences pressure that is induced by surface tension, commonly referred to as the Young-Laplace pressure. Surface tension originates from cohesive forces between molecules, and in the bulk of the fluid, molecules experience attractive forces from all directions. The surface of a fluid is curved because exposed molecules on the surface have fewer neighboring interactions, resulting in a net force that contracts the surface. There exists a pressure difference either side of this curvature, and when this balances out the pressure due to gravity, one can rearrange to find the capillary length.

In the case of a fluid–fluid interface, for example a drop of water immersed in another liquid, the capillary length denoted $\lambda_$ or $l_$ is most commonly given by the formula,

:$\lambda_ = \sqrt$,

where $\gamma$ is the surface tension of the fluid interface, $g$ is the gravitational acceleration and $\Delta\rho$ is the mass density difference of the fluids. The capillary length is sometimes denoted $\kappa^$ in relation to the mathematical notation for curvature. The term capillary constant is somewhat misleading, because it is important to recognize that $\lambda_$ is a composition of variable quantities, for example the value of surface tension will vary with temperature and the density difference will change depending on the fluids involved at an interface interaction. However if these conditions are known, the capillary length can be considered a constant for any given liquid, and be used in numerous fluid mechanical problems to scale the derived equations such that they are valid for any fluid. For molecular fluids, the interfacial tensions and density differences are typically of the order of $10-100$ mN m⁻¹ and $0.1-1$g mL⁻¹ respectively resulting in a capillary length of $\sim3$mm for water and air at room temperature on earth. On the other hand, the capillary length would be $= 6.68$mm for water-air on the moon. For a soap bubble, the surface tension must be divided by the mean thickness, resulting in a capillary length of about $3$ meters in air! The equation for $\lambda_$ can also be found with an extra $\sqrt$ term, most often used when normalising the capillary height.

Origin

Theoretical

One way to theoretically derive the capillary length, is to imagine a liquid droplet at the point where surface tension balances gravity.

Let there be a spherical droplet with radius $\lambda_c$,

The characteristic Laplace pressure $P_$, due to surface tension, is equal to

:$P_=2\frac$,

where $\gamma$ is the surface tension. The pressure due to gravity (hydrostatic pressure) $P_$ of a column of liquid is given by

:$P_=\rho g h=2\rho g\lambda_$,

where $\rho$ is the droplet density, $g$ the gravitational acceleration, and $h=2\lambda_$ is the height of the droplet.

At the point where the Laplace pressure balances out the pressure due to gravity $P_=P_\gamma$,

:$\lambda_ = \sqrt$.

Relationship with the Eötvös number

The above derivation can be used when dealing with the Eötvös number, a dimensionless quantity that represents the ratio between the buoyancy forces and surface tension of the liquid. Despite being introduced by Loránd Eötvös in 1886, he has since become fairly dissociated with it, being replaced with Wilfrid Noel Bond such that it is now referred to as the Bond number in recent literature.

The Bond number can be written such that it includes a characteristic length- normally the radius of curvature of a liquid, and the capillary length

:$\mathrm=\frac$,
with parameters defined above, and $L$ the radius of curvature.

Therefore the bond number can be written as

:$\mathrm=\left(\frac\right)^2$,
with $\lambda_$ the capillary length.

If the bond number is set to 1, then the characteristic length is the capillary length

Experimental

The capillary length can also be found through the manipulation of many different physical phenomenon. One method is to focus on capillary action, which is the attraction of a liquids surface to a surrounding solid.

Association with Jurin's law

Jurin's law is a quantitative law that shows that the maximum height that can be achieved by a liquid in a capillary tube is inversely proportional to the diameter of the tube. The law can be illustrated mathematically during capillary uplift, which is a traditional experiment measuring the height of a liquid in a capillary tube. When a capillary tube is inserted into a liquid, the liquid will rise or fall in the tube, due to an imbalance in pressure. The characteristic height is the distance from the bottom of the meniscus to the base, and exists when the Laplace pressure and the pressure due to gravity are balanced. One can reorganize to show the capillary length as a function of surface tension and gravity.

:$\lambda_^2=\frac$,

with $h$ the height of the liquid, $r$ the radius of the capillary tube, and $\theta$ the contact angle.

The contact angle is defined as the angle formed by the intersection of the liquid-solid interface and the liquid–vapour interface. The size of the angle quantifies the wetability of liquid, i.e., the interaction between the liquid and solid surface. A contact angle of $\theta=0$ can be considered, perfect wetting.

:$\lambda_^2=\frac$.

Thus the $\lambda_^2$ forms a cyclical 3 factor equation with $r, h$.

This property is usually used by physicists to estimate the height a liquid will rise in a particular capillary tube, radius known, without the need for an experiment. When the characteristic height of the liquid is sufficiently less than the capillary length, then the effect of hydrostatic pressure due to gravity can be neglected.

Using the same premises of capillary rise, one can find the capillary length as a function of the volume increase, and wetting perimeter of the capillary walls.

Association with a sessile droplet

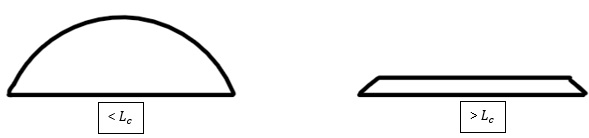
Another way to find the capillary length is using different pressure points inside a sessile droplet, with each point having a radius of curvature, and equate them to the Laplace pressure equation. This time the equation is solved for the height of the meniscus level which again can be used to give the capillary length.

The shape of a sessile droplet is directly proportional to whether the radius is greater than or less than the capillary length. Microdrops are droplets with radius smaller than the capillary length, and their shape is governed solely by surface tension, forming a spherical cap shape. If a droplet has a radius larger than the capillary length, they are known as macrodrops and the gravitational forces will dominate. Macrodrops will be 'flattened' by gravity and the height of the droplet will be reduced.

History

The investigations in capillarity stem back as far as Leonardo da Vinci, however the idea of capillary length was not developed until much later. Fundamentally the capillary length is a product of the work of Thomas Young and Pierre Laplace. They both appreciated that surface tension arose from cohesive forces between particles and that the shape of a liquid's surface reflected the short range of these forces. At the turn of the 19th century they independently derived pressure equations, but due to notation and presentation, Laplace often gets the credit. The equation showed that the pressure within a curved surface between two static fluids is always greater than that outside of a curved surface, but the pressure will decrease to zero as the radius approached infinity. Since the force is perpendicular to the surface and acts towards the centre of the curvature, a liquid will rise when the surface is concave and depress when convex. This was a mathematical explanation of the work published by James Jurin in 1719, where he quantified a relationship between the maximum height taken by a liquid in a capillary tube and its diameter – Jurin's law. The capillary length evolved from the use of the Laplace pressure equation at the point it balanced the pressure due to gravity, and is sometimes called the ''Laplace capillary constant,'' after being introduced by Laplace in 1806.

In nature

Bubbles

Like a droplet, bubbles are round because cohesive forces pull its molecules into the tightest possible grouping, a sphere. Due to the trapped air inside the bubble, it is impossible for the surface area to shrink to zero, hence the pressure inside the bubble is greater than outside, because if the pressures were equal, then the bubble would simply collapse. This pressure difference can be calculated from Laplace's pressure equation,

:$\Delta P=\frac$.

For a soap bubble, there exists two boundary surfaces, internal and external, and therefore two contributions to the excess pressure and Laplace's formula doubles to

:$\Delta P=\frac$.

The capillary length can then be worked out the same way except that the thickness of the film, $e_0$ must be taken into account as the bubble has a hollow center, unlike the droplet which is a solid. Instead of thinking of a droplet where each side is $\lambda_c$ as in the above derivation, for a bubble $m$ is now

:$m=\Delta \rho R^2 e_0$,

with $R$ and $e_0$ the radius and thickness of the bubble respectively.

As above, the Laplace and hydrostatic pressure are equated resulting in

:$R= \frac=\frac$.

Thus the capillary length contributes to a physiochemical limit that dictates the maximum size a soap bubble can take.

See also

* Capillarity
* Surface tension
* Pressure
* Bond number
* Jurin's law
* Young–Laplace equation

References

{{reflist

Fluid dynamics