Cantilever Magnetometry on:
[Wikipedia]
[Google]
[Amazon]
Cantilever magnetometry is the use of a 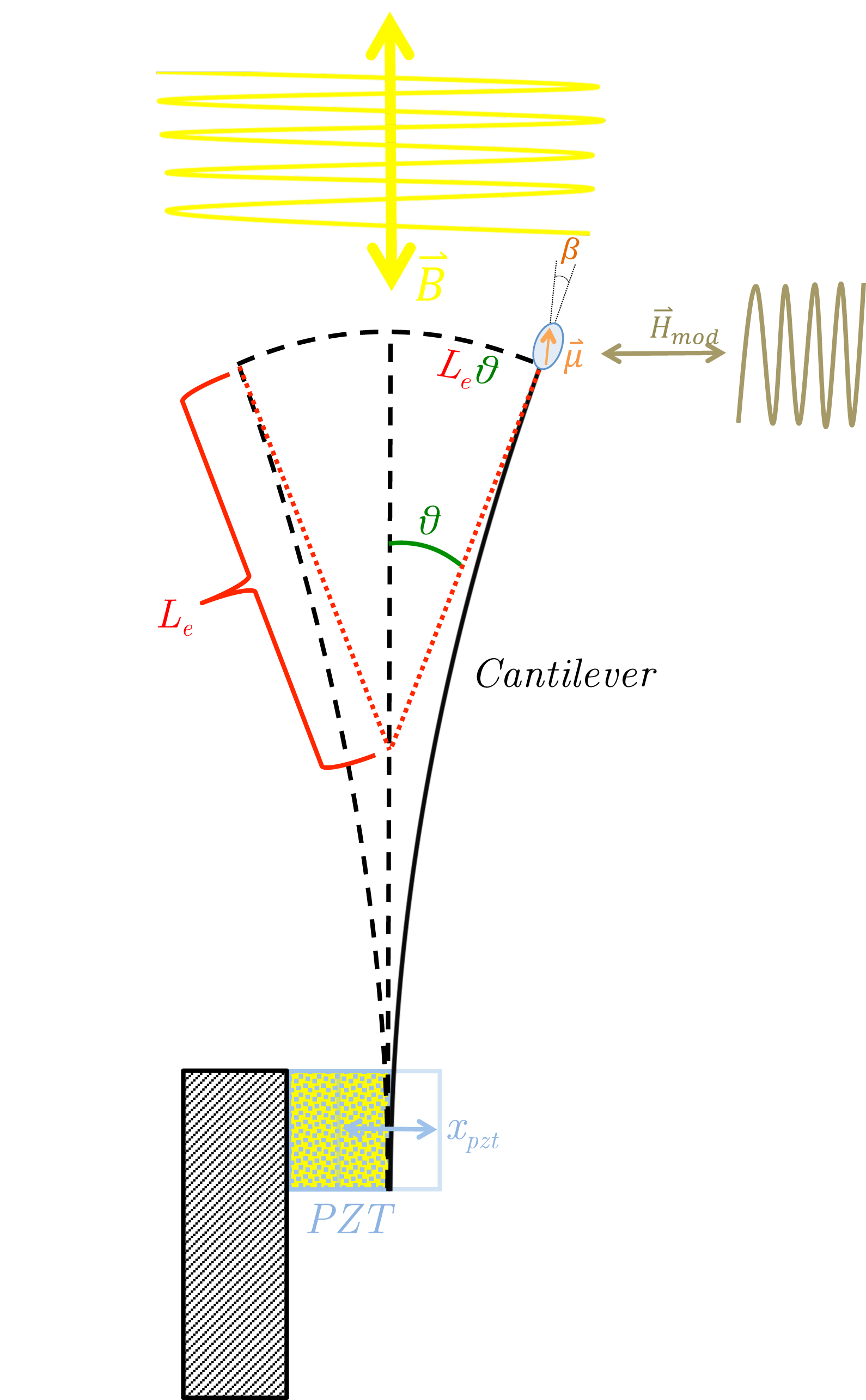 A useful, although limited analogy is that of a pendulum: on earth it oscillates with one frequency, while the same pendulum on, say, the moon, would oscillate with a slower frequency. This is because the mass on the end of the pendulum interacts with the external gravitational field, much as a magnetic moment interacts with an external magnetic field.
A useful, although limited analogy is that of a pendulum: on earth it oscillates with one frequency, while the same pendulum on, say, the moon, would oscillate with a slower frequency. This is because the mass on the end of the pendulum interacts with the external gravitational field, much as a magnetic moment interacts with an external magnetic field.
cantilever
A cantilever is a rigid structural element that extends horizontally and is unsupported at one end. Typically it extends from a flat vertical surface such as a wall, to which it must be firmly attached. Like other structural elements, a cantilev ...
to measure the magnetic moment
In electromagnetism, the magnetic moment or magnetic dipole moment is the combination of strength and orientation of a magnet or other object or system that exerts a magnetic field. The magnetic dipole moment of an object determines the magnitude ...
of magnetic particles. On the end of cantilever is attached a small piece of magnetic
Magnetism is the class of physical attributes that occur through a magnetic field, which allows objects to attract or repel each other. Because both electric currents and magnetic moments of elementary particles give rise to a magnetic field, m ...
material, which interacts with external magnetic fields and exerts torque on the cantilever. These torques cause the cantilever to oscillate faster or slower, depending on the orientation of the particle's moment with respect to the external field, and the magnitude of the moment. The magnitude of the moment and magnetic anisotropy
In condensed matter physics, magnetic anisotropy describes how an object's magnetic properties can be anisotropy, different depending on direction. In the simplest case, there is no preferential direction for an object's magnetic moment. It will ...
of the material can be deduced by measuring the cantilever's oscillation frequency versus external field.
 A useful, although limited analogy is that of a pendulum: on earth it oscillates with one frequency, while the same pendulum on, say, the moon, would oscillate with a slower frequency. This is because the mass on the end of the pendulum interacts with the external gravitational field, much as a magnetic moment interacts with an external magnetic field.
A useful, although limited analogy is that of a pendulum: on earth it oscillates with one frequency, while the same pendulum on, say, the moon, would oscillate with a slower frequency. This is because the mass on the end of the pendulum interacts with the external gravitational field, much as a magnetic moment interacts with an external magnetic field.
Cantilever equation of motion
As the cantilever oscillates back and forth it arches into hyperbolic curves with the salient feature that a tangent to the end of the cantilever always intersects one point along the middle axis. From this we define the effective length of the cantilever, , to be the distance from this point to the end of the cantilever (see image to the right). The Lagrangian for this system is then given by where is the effective cantilever mass, is the volume of the particle, is the cantilever-constant and is the magnetic moment of the particle. To find the equation of motion we note that we have two variables, and so there are two corresponding Lagrangian equations which need to be solved as a system of equations, : where we have defined . We can plug Eq. 1 into our Lagrangian, which then becomes a function of only. Then , and we have : : : or where . The solution to this differential equation is where and are coefficients determined by the initial conditions. The motion of a simple pendulum is similarly described by this differential equation and solution in the small angle approximation. We can use the binomial expansion to rewrite , : which is the form as seen in literature, for example equation 2 in the paper "Magnetic Dissipation and Fluctuations in Individual Nanomagnets Measured by Ultrasensitive Cantilever Magnetometry".References
{{Reflist Magnetometers