Calculus Of Moving Surfaces on:
[Wikipedia]
[Google]
[Amazon]
 The calculus of moving surfaces (CMS) is an extension of the classical
The calculus of moving surfaces (CMS) is an extension of the classical 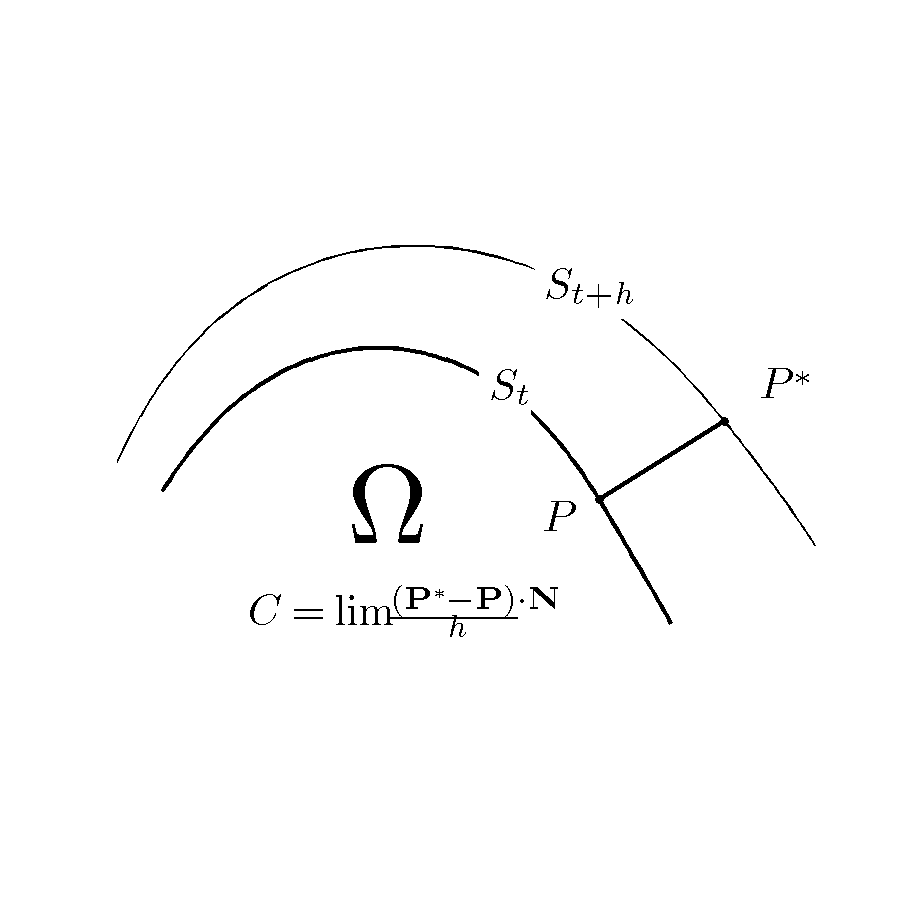
 The tensorial time derivative for a
The tensorial time derivative for a
 The calculus of moving surfaces (CMS) is an extension of the classical
The calculus of moving surfaces (CMS) is an extension of the classical tensor calculus
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects associated with a vector space. Tensors may map between different objects such as vectors, scalars, and even other ...
to deforming manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a N ...
s. Central to the CMS is the tensorial time derivative whose original definition J. Hadamard, Leçons Sur La Propagation Des Ondes Et Les Équations de l'Hydrodynamique. Paris: Hermann, 1903. was put forth by Jacques Hadamard
Jacques Salomon Hadamard (; 8 December 1865 – 17 October 1963) was a French mathematician who made major contributions in number theory, complex analysis, differential geometry, and partial differential equations.
Biography
The son of a tea ...
. It plays the role analogous to that of the covariant derivative
In mathematics and physics, covariance is a measure of how much two variables change together, and may refer to:
Statistics
* Covariance matrix, a matrix of covariances between a number of variables
* Covariance or cross-covariance between ...
on differential manifolds in that it produces a tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects associated with a vector space. Tensors may map between different objects such as vectors, scalars, and even other ...
when applied to a tensor.
Suppose that is the evolution of the surface
A surface, as the term is most generally used, is the outermost or uppermost layer of a physical object or space. It is the portion or region of the object that can first be perceived by an observer using the senses of sight and touch, and is ...
indexed by a time-like parameter . The definitions of the surface velocity
Velocity is a measurement of speed in a certain direction of motion. It is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of physical objects. Velocity is a vector (geometry), vector Physical q ...
and the operator
Operator may refer to:
Mathematics
* A symbol indicating a mathematical operation
* Logical operator or logical connective in mathematical logic
* Operator (mathematics), mapping that acts on elements of a space to produce elements of another sp ...
are the geometric
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
foundations of the CMS. The velocity C is the rate of deformation of the surface in the instantaneous normal direction. The value of at a point is defined as the limit
:
where is the point on that lies on the straight line perpendicular to at point P. This definition is illustrated in the first geometric figure below. The velocity is a signed quantity: it is positive when points in the direction of the chosen normal, and negative otherwise. The relationship between and is analogous to the relationship between location and velocity in elementary calculus: knowing either quantity allows one to construct the other by differentiation or integration
Integration may refer to:
Biology
*Multisensory integration
*Path integration
* Pre-integration complex, viral genetic material used to insert a viral genome into a host genome
*DNA integration, by means of site-specific recombinase technology, ...
.

 The tensorial time derivative for a
The tensorial time derivative for a scalar field
In mathematics and physics, a scalar field is a function associating a single number to each point in a region of space – possibly physical space. The scalar may either be a pure mathematical number ( dimensionless) or a scalar physical ...
F defined on is the rate of change in in the instantaneously normal direction:
:
This definition is also illustrated in second geometric figure.
The above definitions are ''geometric
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
''. In analytical settings, direct application of these definitions may not be possible. The CMS gives ''analytical'' definitions of C and in terms of elementary operations from calculus
Calculus is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithmetic operations.
Originally called infinitesimal calculus or "the ...
and differential geometry
Differential geometry is a Mathematics, mathematical discipline that studies the geometry of smooth shapes and smooth spaces, otherwise known as smooth manifolds. It uses the techniques of Calculus, single variable calculus, vector calculus, lin ...
.
Analytical definitions
For analytical definitions of and , consider the evolution of given by : where are general curvilinear space coordinates and are the surface coordinates. By convention, tensor indices of function arguments are dropped. Thus the above equations contains rather than . The velocity object is defined as thepartial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant (as opposed to the total derivative, in which all variables are allowed to vary). P ...
:
The velocity can be computed most directly by the formula
:
where are the covariant components of the normal vector .
Also, defining the shift tensor representation of the surface's tangent space and the tangent velocity as , then the definition of the derivative for an invariant ''F'' reads
:
where is the covariant derivative on S.
For ''tensors'', an appropriate generalization is needed. The proper definition for a representative tensor reads
:
where are Christoffel symbols
In mathematics and physics, the Christoffel symbols are an array of numbers describing a metric connection. The metric connection is a specialization of the affine connection to surface (topology), surfaces or other manifolds endowed with a metri ...
and is the surface's appropriate temporal symbols ( is a matrix representation of the surface's curvature shape operator)
Properties of the -derivative
The -derivative commutes with contraction, satisfies theproduct rule
In calculus, the product rule (or Leibniz rule or Leibniz product rule) is a formula used to find the derivatives of products of two or more functions. For two functions, it may be stated in Lagrange's notation as (u \cdot v)' = u ' \cdot v ...
for any collection of indices
:
and obeys a chain rule
In calculus, the chain rule is a formula that expresses the derivative of the Function composition, composition of two differentiable functions and in terms of the derivatives of and . More precisely, if h=f\circ g is the function such that h ...
for surface restrictions of spatial tensors:
:
Chain rule shows that the -derivatives of spatial "metrics" vanishes
:
where and are covariant and contravariant metric tensor
In the mathematical field of differential geometry, a metric tensor (or simply metric) is an additional structure on a manifold (such as a surface) that allows defining distances and angles, just as the inner product on a Euclidean space allows ...
s, is the Kronecker delta
In mathematics, the Kronecker delta (named after Leopold Kronecker) is a function of two variables, usually just non-negative integers. The function is 1 if the variables are equal, and 0 otherwise:
\delta_ = \begin
0 &\text i \neq j, \\
1 &\ ...
symbol, and and are the Levi-Civita symbol
In mathematics, particularly in linear algebra, tensor analysis, and differential geometry, the Levi-Civita symbol or Levi-Civita epsilon represents a collection of numbers defined from the sign of a permutation of the natural numbers , for some ...
s. The main article
Main may refer to:
Geography
*Main River (disambiguation), multiple rivers with the same name
*Ma'in, an ancient kingdom in modern-day Yemen
* Main, Iran, a village in Fars Province
*Spanish Main, the Caribbean coasts of mainland Spanish territ ...
on Levi-Civita symbols describes them for Cartesian coordinate systems
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular o ...
. The preceding rule is valid in general coordinates, where the definition of the Levi-Civita symbols must include the square root
In mathematics, a square root of a number is a number such that y^2 = x; in other words, a number whose ''square'' (the result of multiplying the number by itself, or y \cdot y) is . For example, 4 and −4 are square roots of 16 because 4 ...
of the determinant
In mathematics, the determinant is a Scalar (mathematics), scalar-valued function (mathematics), function of the entries of a square matrix. The determinant of a matrix is commonly denoted , , or . Its value characterizes some properties of the ...
of the covariant metric tensor .
Differentiation table for the -derivative
The derivative of the key surface objects leads to highly concise and attractive formulas. When applied to the covariant surfacemetric tensor
In the mathematical field of differential geometry, a metric tensor (or simply metric) is an additional structure on a manifold (such as a surface) that allows defining distances and angles, just as the inner product on a Euclidean space allows ...
and the contravariant metric tensor , the following identities result
:
where and are the doubly covariant and doubly contravariant curvature tensors. These curvature tensors, as well as for the mixed curvature tensor , satisfy
:
The shift tensor and the normal satisfy
:
Finally, the surface Levi-Civita symbol
In mathematics, particularly in linear algebra, tensor analysis, and differential geometry, the Levi-Civita symbol or Levi-Civita epsilon represents a collection of numbers defined from the sign of a permutation of the natural numbers , for some ...
s and satisfy
:
Time differentiation of integrals
The CMS provides rules for time differentiation of volume and surface integrals.See also
*ADM formalism
The Arnowitt–Deser–Misner (ADM) formalism (named for its authors Richard Arnowitt, Stanley Deser and Charles W. Misner) is a Hamiltonian formulation of general relativity that plays an important role in canonical quantum gravity and nume ...
References
{{Reflist Tensors Differential geometry Riemannian geometry Curvature (mathematics) Moving surfaces