Bloch Equations

In physics and chemistry, specifically in nuclear magnetic resonance (NMR), magnetic resonance imaging (MRI), and electron spin resonance (ESR), the Bloch equations are a set of macroscopic equations that are used to calculate the nuclear magnetization M = (''M''_''x'', ''M''_''y'', ''M''_''z'') as a function of time when relaxation times ''T''₁ and ''T''₂ are present. These are phenomenological equations that were introduced by Felix Bloch in 1946. Sometimes they are called the equations of motion of nuclear magnetization. They are analogous to the Maxwell–Bloch equations.

In the laboratory (stationary) frame of reference

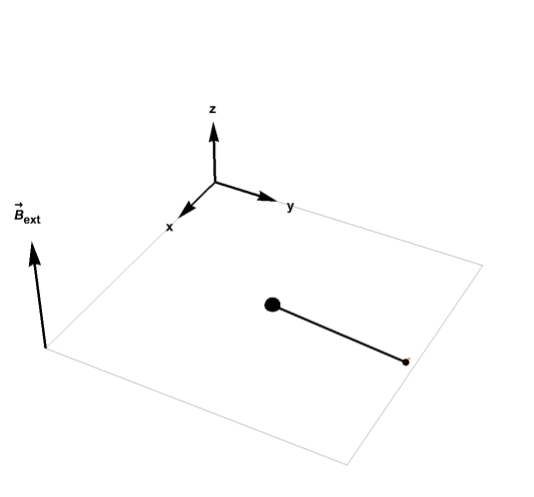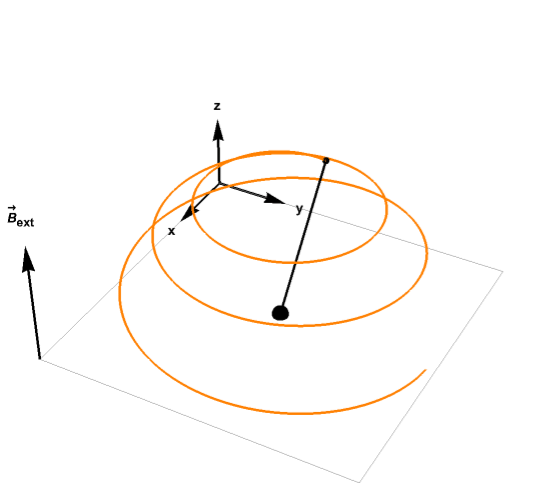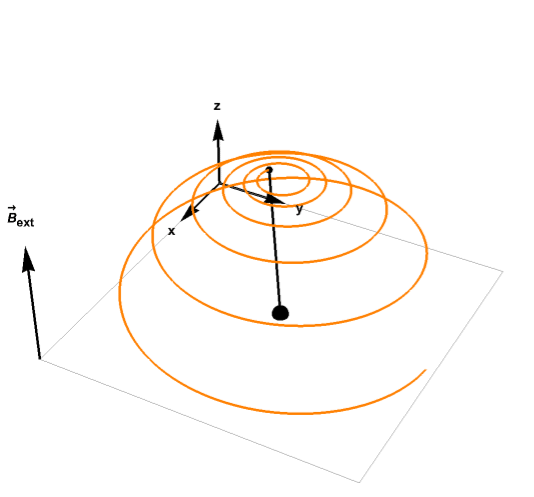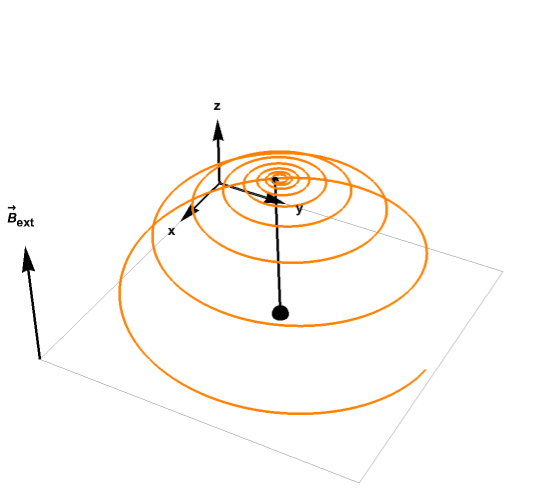
Let M(''t'') = (''M_x''(''t''), ''M_y''(''t''), ''M_z''(''t'')) be the nuclear magnetization. Then the Bloch equations read:

:$\frac = \gamma ( \mathbf (t) \times \mathbf (t) ) _x - \frac$
:$\frac = \gamma ( \mathbf (t) \times \mathbf (t) ) _y - \frac$
:$\frac = \gamma ( \mathbf (t) \times \mathbf (t) ) _z - \frac$

where γ is the gyromagnetic ratio and B(''t'') = (''B''_''x''(''t''), ''B''_''y''(''t''), ''B''₀ + Δ''B''_''z''(t)) is the magnetic field experienced by the nuclei.
The ''z'' component of the magnetic field B is sometimes composed of two terms:
*one, ''B''₀, is constant in time,
*the other one, Δ''B''_''z''(t), may be time dependent. It is present in magnetic resonance imaging and helps with the spatial decoding of the NMR signal.
M(''t'') × B(''t'') is the cross product of these two vectors.
''M''₀ is the steady state nuclear magnetization (that is, for example, when t → ∞); it is in the ''z'' direction.

Physical background

With no relaxation (that is both ''T''₁ and ''T''₂ → ∞) the above equations simplify to:

:$\frac = \gamma ( \mathbf (t) \times \mathbf (t) ) _x$
:$\frac = \gamma ( \mathbf (t) \times \mathbf (t) ) _y$
:$\frac = \gamma ( \mathbf (t) \times \mathbf (t) ) _z$

or, in vector notation:

:$\frac = \gamma \mathbf (t) \times \mathbf (t)$

This is the equation for Larmor precession of the nuclear magnetization ''M'' in an external magnetic field B.

The relaxation terms,

:$\left ( -\frac , -\frac , -\frac \right )$

represent an established physical process of transverse and longitudinal relaxation of nuclear magnetization M.

As macroscopic equations

These equations are not ''microscopic'': they do not describe the equation of motion of individual nuclear magnetic moments. These are governed and described by laws of quantum mechanics.

Bloch equations are ''macroscopic'': they describe the equations of motion of macroscopic nuclear magnetization that can be obtained by summing up all nuclear magnetic moment in the sample.

Alternative forms

Opening the vector product brackets in the Bloch equations leads to:

:$\frac = \gamma \left ( M_y (t) B_z (t) - M_z (t) B_y (t) \right ) - \frac$
:$\frac = \gamma \left ( M_z (t) B_x (t) - M_x (t) B_z (t) \right ) - \frac$
:$\frac = \gamma \left ( M_x (t) B_y (t) - M_y (t) B_x (t) \right ) - \frac$

The above form is further simplified assuming

:$M_ = M_x + iM_y \text B_ = B_x + iB_y\,$

where ''i'' = . After some algebra one obtains:

:$\frac = -i \gamma \left ( M_ (t) B_z (t) - M_z (t) B_ (t) \right ) - \frac$.
:$\frac = i \frac \left ( M_ (t) \overline - \overline (t) B_ (t) \right ) - \frac$

where

:$\overline = M_x - i M_y$.

is the complex conjugate of ''M_xy''. The real and imaginary parts of ''M_xy'' correspond to ''M_x'' and ''M_y'' respectively.
''M_xy'' is sometimes called transverse nuclear magnetization.

Matrix form

The Bloch equations can be recast in matrix-vector notation:
:$\frac\left( \begin M_x\\ M_y\\ M_z \end \right) = \left( \begin -\frac& \gamma B_z & -\gamma B_y \\ -\gamma B_z & -\frac& \gamma B_x \\ \gamma B_y & -\gamma B_x & -\frac \end \right) \left( \begin M_x\\ M_y\\ M_z \end \right) + \left( \begin 0\\ 0\\ \frac \end \right)$

In a rotating frame of reference

In a rotating frame of reference, it is easier to understand the behaviour of the nuclear magnetization M. This is the motivation:

Solution of Bloch equations with ''T''₁, ''T''₂ → ∞

Assume that:
*at ''t'' = 0 the transverse nuclear magnetization ''M''_xy(0) experiences a constant magnetic field B(''t'') = (0, 0, ''B''₀);
*''B''₀ is positive;
*there are no longitudinal and transverse relaxations (that is ''T''₁ and ''T''₂ → ∞).

Then the Bloch equations are simplified to:

:$\frac = -i \gamma M_ (t) B_$,
:$\frac = 0$.

These are two (not coupled) linear differential equations. Their solution is:

:$M_(t) = M_ (0) e^$,
:$M_z(t) = M_0 = \text \,$.

Thus the transverse magnetization, ''M''_xy, rotates around the ''z'' axis with angular frequency ω₀ = γ''B''₀ in clockwise direction (this is due to the negative sign in the exponent).
The longitudinal magnetization, ''M''_z remains constant in time. This is also how the transverse magnetization appears to an observer in the laboratory frame of reference (that is to a stationary observer).

''M''_xy(''t'') is translated in the following way into observable quantities of ''M''_x(''t'') and ''M''_y(''t''): Since

:M_(t) = M_ (0) e^ = M_ (0) \left \cos (\omega _0 t) - i \sin (\omega_0 t) \right /math>

then

:$M_(t) = \text \left (M_ (t) \right ) = M_ (0) \cos (\omega _0 t)$,
:$M_(t) = \text \left (M_ (t) \right ) = -M_ (0) \sin (\omega _0 t)$,

where Re(''z'') and Im(''z'') are functions that return the real and imaginary part of complex number ''z''. In this calculation it was assumed that ''M''_xy(0) is a real number.

Transformation to rotating frame of reference

This is the conclusion of the previous section: in a constant magnetic field ''B''₀ along ''z'' axis the transverse magnetization ''M''_xy rotates around this axis in clockwise direction with angular frequency ω₀. If the observer were rotating around the same axis in clockwise direction with angular frequency Ω, ''M''_xy it would appear to her or him rotating with angular frequency ω₀ - Ω. Specifically, if the observer were rotating around the same axis in
clockwise direction with angular frequency ω₀, the transverse magnetization ''M''_xy would appear to her or him stationary.

This can be expressed mathematically in the following way:
* Let (''x'', ''y'', ''z'') the Cartesian coordinate system of the laboratory (or stationary) frame of reference, and
* (''x''′, ''y''′, ''z''′) = (''x''′, ''y''′, ''z'') be a Cartesian coordinate system that is rotating around the ''z'' axis of the laboratory frame of reference with angular frequency Ω. This is called the rotating frame of reference. Physical variables in this frame of reference will be denoted by a prime.

Obviously:

:$M_z' (t) = M_z(t)\,$.

What is ''M_xy''′(''t'')? Expressing the argument at the beginning of this section in a mathematical way:

:$M_'(t) = e^ M_(t)\,$.

Equation of motion of transverse magnetization in rotating frame of reference

What is the equation of motion of ''M_xy''′(''t'')?

:$\frac = \frac = e^ \frac + i \Omega e^ M_(t) = e^ \frac + i \Omega M_'(t)$

Substitute from the Bloch equation in laboratory frame of reference:

:\begin \frac & = e^ \left i \gamma \left ( M_ (t) B_z (t) - M_z (t) B_ (t) \right ) -
\frac \right + i \Omega M_'(t) \\

& = \left i \gamma \left ( M_ (t) e^ B_z (t) - M_z (t) B_ (t) e^\right ) -
\frac \right + i \Omega M_'(t) \\

& = -i \gamma \left ( M_' (t) B_z (t) - M_z (t) B_' (t) \right ) + i \Omega M_'(t) -
\frac \\

\end

But by assumption in the previous section: ''B''_z′(''t'') = ''B''_z(''t'') = ''B''₀ + Δ''B''_z(''t'') and ''M''_z(''t'') = ''M_z′(''t''). Substituting into the equation above:

:$\begin \frac & = -i \gamma \left ( M_' (t) (B_0 + \Delta B_z(t)) - M_z' (t) B_' (t) \right ) + i \Omega M_'(t) - \frac \\ & = -i \gamma B_0 M_'(t) - i \gamma \Delta B_z(t) M_'(t) + i \gamma B_' (t) M_z' (t)+ i \Omega M_'(t) - \frac \\ & = i (\Omega - \omega_0) M_'(t) - i \gamma \Delta B_z(t) M_'(t) + i \gamma B_' (t) M_z' (t) - \frac \\ \end$

This is the meaning of terms on the right hand side of this equation:
* ''i'' (Ω - ω₀) ''M''_xy′(''t'') is the Larmor term in the frame of reference rotating with angular frequency Ω. Note that it becomes zero when Ω = ω₀.
* The -''i'' γ Δ''B''_z(''t'') ''M''_xy′(''t'') term describes the effect of magnetic field inhomogeneity (as expressed by Δ''B''_z(''t'')) on the transverse nuclear magnetization; it is used to explain ''T''₂^*. It is also the term that is behind MRI: it is generated by the gradient coil system.
* The ''i'' γ ''B''_xy′(''t'') ''M''_z(''t'') describes the effect of RF field (the ''B''_xy′(''t'') factor) on nuclear magnetization. For an example see below.
* - ''M''_xy′(''t'') / ''T''₂ describes the loss of coherency of transverse magnetization.

Similarly, the equation of motion of ''M_z'' in the rotating frame of reference is:
:$\frac = i \frac \left ( M'_ (t) \overline - \overline (t) B'_ (t) \right ) - \frac$

Time independent form of the equations in the rotating frame of reference

When the external field has the form:

:$B_x(t) = B_1 \cos \omega t$
:$B_y(t) = -B_1 \sin \omega t$
:$B_z(t) = B_0$,

We define:
:$\epsilon=\gamma B_1$ and :$\Delta=\gamma B_0-\omega$ ,
and get (in the matrix-vector notation):

:$\frac\left( \begin M'_x\\ M'_y\\ M'_z \end \right) = \left( \begin -\frac& \Delta & -\epsilon\\ -\Delta & -\frac& \epsilon\\ -\epsilon & -\epsilon & -\frac \end \right) \left( \begin M'_x\\ M'_y\\ M'_z \end \right) + \left( \begin 0\\ 0\\ \frac \end \right)$

Simple solutions

Relaxation of transverse nuclear magnetization ''M_xy''

Assume that:
* The nuclear magnetization is exposed to constant external magnetic field in the ''z'' direction ''B''_z′(''t'') = ''B''_z(''t'') = ''B''₀. Thus ω₀ = γ''B''₀ and Δ''B''_z(''t'') = 0.
* There is no RF, that is ''B''_xy' = 0.
* The rotating frame of reference rotates with an angular frequency Ω = ω₀.

Then in the rotating frame of reference, the equation of motion for the transverse nuclear magnetization, ''M''_xy'(''t'') simplifies to:

:$\frac = - \frac$

This is a linear ordinary differential equation and its solution is

:$M_'(t) = M_'(0) e^$.

where ''M''_xy'(0) is the transverse nuclear magnetization in the rotating frame at time ''t'' = 0. This is the initial condition for the differential equation.

Note that when the rotating frame of reference rotates ''exactly'' at the Larmor frequency (this is the physical meaning of the above assumption Ω = ω₀), the vector of transverse nuclear magnetization, ''M''_xy(''t'') appears to be stationary.

Relaxation of longitudinal nuclear magnetization ''M_z''

Assume that:
* The nuclear magnetization is exposed to constant external magnetic field in the ''z'' direction ''B''_z′(''t'') = ''B''_z(''t'') = ''B''₀. Thus ω₀ = γ''B''₀ and Δ''B''_z(''t'') = 0.
* There is no RF, that is ''B''_xy' = 0.
* The rotating frame of reference rotates with an angular frequency Ω = ω₀.

Then in the rotating frame of reference, the equation of motion for the longitudinal nuclear magnetization, ''M''_z(''t'') simplifies to:

:$\frac = - \frac$

This is a linear ordinary differential equation and its solution is

:M_z(t) = M_ - _ - M_z(0)^

where ''M''_z(0) is the longitudinal nuclear magnetization in the rotating frame at time ''t'' = 0. This is the initial condition for the differential equation.

90 and 180° RF pulses

Assume that:
* Nuclear magnetization is exposed to constant external magnetic field in ''z'' direction ''B''_z′(''t'') = ''B''_z(''t'') = ''B''₀. Thus ω₀ = γ''B''₀ and Δ''B''_z(''t'') = 0.
* At ''t'' = 0 an RF pulse of constant amplitude and frequency ω₀ is applied. That is ''B'_xy''(''t'') = ''B'_xy'' is constant. Duration of this pulse is τ.
* The rotating frame of reference rotates with an angular frequency Ω = ω₀.
* ''T''₁ and ''T''₂ → ∞. Practically this means that τ ≪ ''T''₁ and ''T''₂.

Then for 0 ≤ ''t'' ≤ τ:

:$\begin \frac = i \gamma B_' M_z (t) \end$
:$\frac = i \frac \left ( M'_ (t) \overline - \overline (t) B'_ \right )$

See also

*The Bloch–Torrey equation is a generalization of the Bloch equations, which includes added terms due to the transfer of magnetization by diffusion.
(1956)

References

Further reading

* Charles Kittel, ''Introduction to Solid State Physics'', John Wiley & Sons, 8th edition (2004), . Chapter 13 is on Magnetic Resonance.

{{DEFAULTSORT:Bloch Equations
Nuclear magnetic resonance
Magnetic resonance imaging