Biryukov Equation

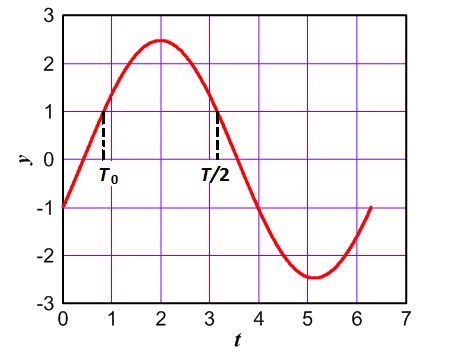In the study of dynamical systems, the Biryukov equation (or Biryukov oscillator), named after Vadim Biryukov (1946), is a non-linear second-order differential equation used to model damped oscillators.

The equation is given by
$\frac+f(y)\frac+y=0, \qquad\qquad (1)$

where is a piecewise constant function which is positive, except for small as

\begin
& f(y) = \begin -F, & , y, \le Y_0; \\ ptF, & , y, >Y_0. \end \\ pt& F = \text > 0, \quad Y_0 = \text > 0.
\end

Eq. (1) is a special case of the Lienard equation; it describes the auto-oscillations.

Solution (1) at separate time intervals when f(y) is constant is given by

$y_k(t) = A_\exp(s_t) + A_\exp(s_t) \qquad\qquad (2)$

where denotes the exponential function. Here
s_k = \begin
\displaystyle \frac\mp\sqrt, & , y, pt\displaystyle -\frac\mp\sqrt & \text
\end
Expression (2) can be used for real and complex values of .

The first half-period’s solution at $y(0)=\pm Y_0$ is

\begin
y(t) &= \begin
y_1(t), & 0\le tpt
y_2(t), & \displaystyle T_0\le t< \frac. \end \\ pt
y_1(t) &= A_\cdot \exp (s_t)+A_\cdot \exp (s_t), \\ pty_2(t) &= A_\cdot \exp(s_t)+A_\cdot \exp (s_t).
\end

The second half-period’s solution is

y(t)= \begin
\displaystyle -y_1\left(t-\frac\right), & \displaystyle \frac \le t < \frac + T_0; \\ pt
\displaystyle -y_2\left(t-\frac\right), & \displaystyle \frac + T_0 \le t < T. \end

The solution contains four constants of integration , the period and the boundary between and needs to be found. A boundary condition is derived from the continuity of and .Pilipenko A. M., and Biryukov V. N. «Investigation of Modern Numerical Analysis Methods of Self-Oscillatory Circuits Efficiency», Journal of Radio Electronics, No 9, (2013). http://jre.cplire.ru/jre/aug13/9/text-engl.html

Solution of (1) in the stationary mode thus is obtained by solving a system of algebraic equations as

\begin
& y_1(0) = -Y_0 & y_1(T_0) = Y_0 \\ pt& y_2(T_0) = Y_0 & y_2 \! \left(\tfrac\right) = Y_0 \\ pt& \displaystyle \left.\frac\_ = \left.\frac\_ \qquad
& \displaystyle \left.\frac\_ = -\left.\frac\_\frac
\end

The integration constants are obtained by the Levenberg–Marquardt algorithm.
With $f(y)=\mu(-1+y^2)$, $\mu = \text > 0,$ Eq. (1) named Van der Pol oscillator. Its solution cannot be expressed by elementary functions in closed form.

References

{{Reflist

Differential equations
Analog circuits