Bicorn on:
[Wikipedia]
[Google]
[Amazon]
 In
In
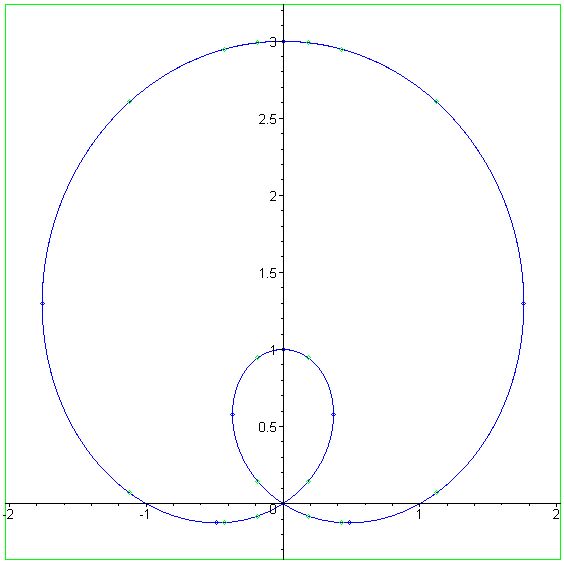 The bicorn is a
The bicorn is a
geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, the bicorn, also known as a cocked hat curve due to its resemblance to a bicorne
The bicorne or bicorn (two-cornered) is a historical form of hat widely adopted in the 1790s as an item of uniform by European and American army and naval officers. Most generals and staff officers of the Napoleonic period wore bicornes, whic ...
, is a rational
Rationality is the quality of being guided by or based on reason. In this regard, a person acts rationally if they have a good reason for what they do, or a belief is rational if it is based on strong evidence. This quality can apply to an ...
quartic curve defined by the equation
It has two cusp
A cusp is the most pointed end of a curve. It often refers to cusp (anatomy), a pointed structure on a tooth.
Cusp or CUSP may also refer to:
Mathematics
* Cusp (singularity), a singular point of a curve
* Cusp catastrophe, a branch of bifu ...
s and is symmetric about the y-axis.
History
In 1864,James Joseph Sylvester
James Joseph Sylvester (3 September 1814 – 15 March 1897) was an English mathematician. He made fundamental contributions to matrix theory, invariant theory, number theory, partition theory, and combinatorics. He played a leadership ...
studied the curve
in connection with the classification of quintic equation
In mathematics, a quintic function is a function of the form
:g(x)=ax^5+bx^4+cx^3+dx^2+ex+f,\,
where , , , , and are members of a field, typically the rational numbers, the real numbers or the complex numbers, and is nonzero. In other word ...
s; he named the curve a bicorn because it has two cusps. This curve was further studied by Arthur Cayley
Arthur Cayley (; 16 August 1821 – 26 January 1895) was a British mathematician who worked mostly on algebra. He helped found the modern British school of pure mathematics, and was a professor at Trinity College, Cambridge for 35 years.
He ...
in 1867.
Properties
 The bicorn is a
The bicorn is a plane algebraic curve
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane cu ...
of degree four and genus
Genus (; : genera ) is a taxonomic rank above species and below family (taxonomy), family as used in the biological classification of extant taxon, living and fossil organisms as well as Virus classification#ICTV classification, viruses. In bino ...
zero. It has two cusp singularities in the real plane, and a double point in the complex projective plane
In mathematics, the complex projective plane, usually denoted or is the two-dimensional complex projective space. It is a complex manifold of complex dimension 2, described by three complex coordinates
:(Z_1,Z_2,Z_3) \in \C^3, \qquad (Z_1,Z_2, ...
at . If we move and to the origin and perform an imaginary rotation on by substituting for and for in the bicorn curve, we obtain
This curve, a limaçon
In geometry, a limaçon or limacon , also known as a limaçon of Pascal or Pascal's Snail, is defined as a roulette curve formed by the path of a point fixed to a circle when that circle rolls around the outside of a circle of equal radius. I ...
, has an ordinary double point at the origin, and two nodes in the complex plane, at and .
The parametric equation
In mathematics, a parametric equation expresses several quantities, such as the coordinates of a point (mathematics), point, as Function (mathematics), functions of one or several variable (mathematics), variables called parameters.
In the case ...
s of a bicorn curve are
with
See also
*List of curves
This is a list of Wikipedia articles about curves used in different fields: mathematics (including geometry, statistics, and applied mathematics), physics, engineering, economics, medicine, biology, psychology, ecology, etc.
Mathematics (Geometry) ...
References
External links
* {{MathWorld, title=Bicorn, urlname=Bicorn Plane curves Quartic curves