Bhāskara I's Sine Approximation Formula on:
[Wikipedia]
[Google]
[Amazon]
In
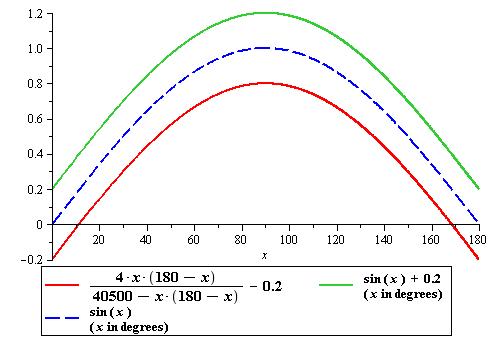
 The formula is applicable for values of ''x''° in the range from 0° to 180°. The formula is remarkably accurate in this range. The graphs of sin ''x'' and the approximation formula are visually indistinguishable and are nearly identical. One of the accompanying figures gives the graph of the error function, namely, the function
:
in using the formula. It shows that the maximum absolute error in using the formula is around 0.0016. From a plot of the percentage value of the absolute error, it is clear that the maximum relative error is less than 1.8%. The approximation formula thus gives sufficiently accurate values of sines for most practical purposes. However, it was not sufficient for the more accurate computational requirements of astronomy. The search for more accurate formulas by Indian astronomers eventually led to the discovery of the
The formula is applicable for values of ''x''° in the range from 0° to 180°. The formula is remarkably accurate in this range. The graphs of sin ''x'' and the approximation formula are visually indistinguishable and are nearly identical. One of the accompanying figures gives the graph of the error function, namely, the function
:
in using the formula. It shows that the maximum absolute error in using the formula is around 0.0016. From a plot of the percentage value of the absolute error, it is clear that the maximum relative error is less than 1.8%. The approximation formula thus gives sufficiently accurate values of sines for most practical purposes. However, it was not sufficient for the more accurate computational requirements of astronomy. The search for more accurate formulas by Indian astronomers eventually led to the discovery of the
 The part of the graph of sin ''x'' in the range from 0° to 180° "looks like" part of a parabola through the points (0, 0) and (180, 0). The general form of such a parabola is
:
The parabola that also passes through (90, 1) (which is the point corresponding to the value sin(90°) = 1) is
:
The parabola which also passes through (30, 1/2) (which is the point corresponding to the value sin(30°) = 1/2) is
:
These expressions suggest a varying denominator which takes the value 90 × 90 when ''x'' = 90 and the value when ''x'' = 30. That this expression should also be symmetrical about the line ''x'' = 90 rules out the possibility of choosing a linear expression in ''x''. Computations involving ''x''(180 − ''x'') might immediately suggest that the expression could be of the form
:
A little experimentation (or by setting up and solving two linear equations in ''a'' and ''b'') will yield the values ''a'' = 5/4, ''b'' = −1/4. These give Bhāskara I's sine approximation formula.
Karel Stroethoff (2014) offers a similar, but simpler argument for Bhāskara I's choice. He also provides an analogous approximation for the cosine and extends the technique to second and third-order polynomials.
The part of the graph of sin ''x'' in the range from 0° to 180° "looks like" part of a parabola through the points (0, 0) and (180, 0). The general form of such a parabola is
:
The parabola that also passes through (90, 1) (which is the point corresponding to the value sin(90°) = 1) is
:
The parabola which also passes through (30, 1/2) (which is the point corresponding to the value sin(30°) = 1/2) is
:
These expressions suggest a varying denominator which takes the value 90 × 90 when ''x'' = 90 and the value when ''x'' = 30. That this expression should also be symmetrical about the line ''x'' = 90 rules out the possibility of choosing a linear expression in ''x''. Computations involving ''x''(180 − ''x'') might immediately suggest that the expression could be of the form
:
A little experimentation (or by setting up and solving two linear equations in ''a'' and ''b'') will yield the values ''a'' = 5/4, ''b'' = −1/4. These give Bhāskara I's sine approximation formula.
Karel Stroethoff (2014) offers a similar, but simpler argument for Bhāskara I's choice. He also provides an analogous approximation for the cosine and extends the technique to second and third-order polynomials.
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, Bhāskara I's sine approximation formula is a rational expression in one variable for the computation
A computation is any type of arithmetic or non-arithmetic calculation that is well-defined. Common examples of computation are mathematical equation solving and the execution of computer algorithms.
Mechanical or electronic devices (or, hist ...
of the approximate values of the trigonometric sines discovered by Bhāskara I
Bhāskara (; commonly called Bhāskara I to avoid confusion with the 12th-century mathematician Bhāskara II) was a 7th-century Indian mathematician and astronomer who was the first to write numbers in the Hindu–Arabic decimal system with a ...
(c. 600 – c. 680), a seventh-century Indian mathematician
A mathematician is someone who uses an extensive knowledge of mathematics in their work, typically to solve mathematical problems. Mathematicians are concerned with numbers, data, quantity, mathematical structure, structure, space, Mathematica ...
.
This formula
In science, a formula is a concise way of expressing information symbolically, as in a mathematical formula or a ''chemical formula''. The informal use of the term ''formula'' in science refers to the general construct of a relationship betwe ...
is given in his treatise titled ''Mahabhaskariya''. It is not known how Bhāskara I arrived at his approximation formula. However, several historian
A historian is a person who studies and writes about the past and is regarded as an authority on it. Historians are concerned with the continuous, methodical narrative and research of past events as relating to the human species; as well as the ...
s of mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
have put forward different hypotheses as to the method Bhāskara might have used to arrive at his formula. The formula is elegant and simple, and it enables the computation of reasonably accurate values of trigonometric sines without the use of geometry.
Approximation formula
The formula is given in verses 17–19, chapter VII, Mahabhaskariya of Bhāskara I. A translation of the verses is given below:(Now) I briefly state the rule (for finding the ''bhujaphala'' and the ''kotiphala'', etc.) without making use of the Rsine-differences 225, etc. Subtract the degrees of a ''bhuja'' (or ''koti'') from the degrees of a half circle (that is, 180 degrees). Then multiply the remainder by the degrees of the ''bhuja'' or ''koti'' and put down the result at two places. At one place subtract the result from 40500. By one-fourth of the remainder (thus obtained), divide the result at the other place as multiplied by the ''anthyaphala'' (that is, the epicyclic radius). Thus is obtained the entire ''bahuphala'' (or, ''kotiphala'') for the sun, moon or the star-planets. So also are obtained the direct and inverse Rsines.(The reference "Rsine-differences 225" is an allusion to Aryabhata's sine table.) In modern mathematical notations, for an angle ''x'' in degrees, this formula gives :
Equivalent forms of the formula
Bhāskara I's sine approximation formula can be expressed using theradian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at ...
measure of angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two R ...
s as follows:
:
For a positive integer ''n'' this takes the following form: (p.60)
:
The formula acquires an even simpler form when expressed in terms of the cosine rather than the sine. Using radian measure for angles from to and putting , one gets
:
To express the previous formula with the constant one can use
:
Equivalent forms of Bhāskara I's formula have been given by almost all subsequent astronomers and mathematicians of India. For example, Brahmagupta
Brahmagupta ( – ) was an Indian Indian mathematics, mathematician and Indian astronomy, astronomer. He is the author of two early works on mathematics and astronomy: the ''Brāhmasphuṭasiddhānta'' (BSS, "correctly established Siddhanta, do ...
's (598–668 CE)
''Brhma-Sphuta-Siddhanta'' (verses 23–24, chapter XIV) gives the formula in the following form:
:
Also, Bhāskara II
Bhāskara II ('; 1114–1185), also known as Bhāskarāchārya (), was an Indian people, Indian polymath, Indian mathematicians, mathematician, astronomer and engineer. From verses in his main work, Siddhānta Śiromaṇi, it can be inferre ...
(1114–1185 CE) has given this formula in his Lilavati (Kshetra-vyavahara, Soka No. 48) in the following form:
:
The approximation can also be used to derive formulas for inverse cosine and inverse sine:
: , and
: .
: , and
: .
Alternatively, using absolute values and the Sign function
In mathematics, the sign function or signum function (from '' signum'', Latin for "sign") is a function that has the value , or according to whether the sign of a given real number is positive or negative, or the given number is itself zer ...
, each pair of functions can be rewritten as such:
:
:
Accuracy of the formula

 The formula is applicable for values of ''x''° in the range from 0° to 180°. The formula is remarkably accurate in this range. The graphs of sin ''x'' and the approximation formula are visually indistinguishable and are nearly identical. One of the accompanying figures gives the graph of the error function, namely, the function
:
in using the formula. It shows that the maximum absolute error in using the formula is around 0.0016. From a plot of the percentage value of the absolute error, it is clear that the maximum relative error is less than 1.8%. The approximation formula thus gives sufficiently accurate values of sines for most practical purposes. However, it was not sufficient for the more accurate computational requirements of astronomy. The search for more accurate formulas by Indian astronomers eventually led to the discovery of the
The formula is applicable for values of ''x''° in the range from 0° to 180°. The formula is remarkably accurate in this range. The graphs of sin ''x'' and the approximation formula are visually indistinguishable and are nearly identical. One of the accompanying figures gives the graph of the error function, namely, the function
:
in using the formula. It shows that the maximum absolute error in using the formula is around 0.0016. From a plot of the percentage value of the absolute error, it is clear that the maximum relative error is less than 1.8%. The approximation formula thus gives sufficiently accurate values of sines for most practical purposes. However, it was not sufficient for the more accurate computational requirements of astronomy. The search for more accurate formulas by Indian astronomers eventually led to the discovery of the power series
In mathematics, a power series (in one variable) is an infinite series of the form
\sum_^\infty a_n \left(x - c\right)^n = a_0 + a_1 (x - c) + a_2 (x - c)^2 + \dots
where ''a_n'' represents the coefficient of the ''n''th term and ''c'' is a co ...
expansions of sin ''x'' and cos ''x'' by Madhava of Sangamagrama
Mādhava of Sangamagrāma (Mādhavan) Availabl/ref> () was an Indian mathematician and astronomer who is considered to be the founder of the Kerala school of astronomy and mathematics in the Late Middle Ages. Madhava made pioneering contributio ...
(c. 1350 – c. 1425), the founder of the Kerala school of astronomy and mathematics
The Kerala school of astronomy and mathematics or the Kerala school was a school of Indian mathematics, mathematics and Indian astronomy, astronomy founded by Madhava of Sangamagrama in Kingdom of Tanur, Tirur, Malappuram district, Malappuram, K ...
.
Derivation of the formula
Bhāskara had not indicated any method by which he arrived at his formula. Historians have speculated on various possibilities. No definitive answers have as yet been obtained. Beyond its historical importance of being a prime example of the mathematical achievements of ancient Indian astronomers, the formula is of significance from a modern perspective also. Mathematicians have attempted to derive the rule using modern concepts and tools. Around half a dozen methods have been suggested, each based on a separate set of premises. (p.104) Most of these derivations use only elementary concepts.Derivation based on elementary geometry
Let thecircumference
In geometry, the circumference () is the perimeter of a circle or ellipse. The circumference is the arc length of the circle, as if it were opened up and straightened out to a line segment. More generally, the perimeter is the curve length arou ...
of a circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
be measured in degrees and let the radius
In classical geometry, a radius (: radii or radiuses) of a circle or sphere is any of the line segments from its Centre (geometry), center to its perimeter, and in more modern usage, it is also their length. The radius of a regular polygon is th ...
''R'' of the circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is cal ...
be also measured in degrees. Choosing a fixed diameter ''AB'' and an arbitrary point ''P'' on the circle and dropping the perpendicular ''PM'' to ''AB'', we can compute the area of the triangle ''APB'' in two ways. Equating the two expressions for the area one gets . This gives
:
Letting ''x'' be the length of the arc ''AP'', the length of the arc ''BP'' is . These arcs are much bigger than the respective chords. Hence one gets
:
One now seeks two constants α and β such that
:
It is indeed not possible to obtain such constants. However, one may choose values for α and β so that the above expression is valid for two chosen values of the arc length ''x''. Choosing 30° and 90° as these values and solving the resulting equations, one immediately gets Bhāskara I's sine approximation formula.
Derivation starting with a general rational expression
Assuming that ''x'' is in radians, one may seek an approximation to sin ''x'' in the following form: : The constants ''a'', ''b'', ''c'', ''p'', ''q'' and ''r'' (only five of them are independent) can be determined by assuming that the formula must be exactly valid when ''x'' = 0, π/6, π/2, π, and further assuming that it has to satisfy the property that sin(''x'') = sin(π − ''x''). This procedure produces the formula expressed usingradian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. It is defined such that one radian is the angle subtended at ...
measure of angles.
An elementary argument
 The part of the graph of sin ''x'' in the range from 0° to 180° "looks like" part of a parabola through the points (0, 0) and (180, 0). The general form of such a parabola is
:
The parabola that also passes through (90, 1) (which is the point corresponding to the value sin(90°) = 1) is
:
The parabola which also passes through (30, 1/2) (which is the point corresponding to the value sin(30°) = 1/2) is
:
These expressions suggest a varying denominator which takes the value 90 × 90 when ''x'' = 90 and the value when ''x'' = 30. That this expression should also be symmetrical about the line ''x'' = 90 rules out the possibility of choosing a linear expression in ''x''. Computations involving ''x''(180 − ''x'') might immediately suggest that the expression could be of the form
:
A little experimentation (or by setting up and solving two linear equations in ''a'' and ''b'') will yield the values ''a'' = 5/4, ''b'' = −1/4. These give Bhāskara I's sine approximation formula.
Karel Stroethoff (2014) offers a similar, but simpler argument for Bhāskara I's choice. He also provides an analogous approximation for the cosine and extends the technique to second and third-order polynomials.
The part of the graph of sin ''x'' in the range from 0° to 180° "looks like" part of a parabola through the points (0, 0) and (180, 0). The general form of such a parabola is
:
The parabola that also passes through (90, 1) (which is the point corresponding to the value sin(90°) = 1) is
:
The parabola which also passes through (30, 1/2) (which is the point corresponding to the value sin(30°) = 1/2) is
:
These expressions suggest a varying denominator which takes the value 90 × 90 when ''x'' = 90 and the value when ''x'' = 30. That this expression should also be symmetrical about the line ''x'' = 90 rules out the possibility of choosing a linear expression in ''x''. Computations involving ''x''(180 − ''x'') might immediately suggest that the expression could be of the form
:
A little experimentation (or by setting up and solving two linear equations in ''a'' and ''b'') will yield the values ''a'' = 5/4, ''b'' = −1/4. These give Bhāskara I's sine approximation formula.
Karel Stroethoff (2014) offers a similar, but simpler argument for Bhāskara I's choice. He also provides an analogous approximation for the cosine and extends the technique to second and third-order polynomials.
See also
* Aryabhata's sine table *Madhava's sine table
Madhava's sine table is the table of trigonometric sines constructed by the 14th century Kerala mathematician-astronomer Madhava of Sangamagrama (c. 1340 – c. 1425). The table lists the jya-s or Rsines of the twenty-four angles from 3.7 ...
* Brahmagupta's interpolation formula Brahmagupta's interpolation formula is a second-order polynomial interpolation formula developed by the Indian mathematician and astronomer Brahmagupta (598–668 CE) in the early 7th century CE. The Sanskrit couplet describing the formula can be ...
References
{{ReflistFurther references
# R.C..Gupta, On derivation of Bhāskara I's formula for the sine, Ganita Bharati 8 (1-4) (1986), 39–41. # T. Hayashi, A note on Bhāskara I's rational approximation to sine, Historia Sci. No. 42 (1991), 45–48. # K. Stroethoff, Bhāskara's approximation for the sine, The Mathematics Enthusiast, Vol. 11, No. 3 (2014), 485–492. Trigonometry Indian mathematics History of mathematics History of geometry