Base Space

In mathematics, and particularly topology, a fiber bundle ( ''Commonwealth English'': fibre bundle) is a space that is a product space, but may have a different topological structure. Specifically, the similarity between a space $E$ and a product space $B \times F$ is defined using a continuous surjective map, $\pi : E \to B,$ that in small regions of $E$ behaves just like a projection from corresponding regions of $B \times F$ to $B.$ The map $\pi,$ called the projection or submersion of the bundle, is regarded as part of the structure of the bundle. The space $E$ is known as the total space of the fiber bundle, $B$ as the base space, and $F$ the fiber.

In the '' trivial'' case, $E$ is just $B \times F,$ and the map $\pi$ is just the projection from the product space to the first factor. This is called a trivial bundle. Examples of non-trivial fiber bundles include the Möbius strip and Klein bottle, as well as nontrivial covering spaces. Fiber bundles, such as the tangent bundle of a manifold and other more general vector bundles, play an important role in differential geometry and differential topology, as do principal bundles.

Mappings between total spaces of fiber bundles that "commute" with the projection maps are known as bundle maps, and the class of fiber bundles forms a category with respect to such mappings. A bundle map from the base space itself (with the identity mapping as projection) to $E$ is called a section of $E.$ Fiber bundles can be specialized in a number of ways, the most common of which is requiring that the transition maps between the local trivial patches lie in a certain topological group, known as the structure group, acting on the fiber $F$.

History

In topology, the terms ''fiber'' (German: ''Faser'') and ''fiber space'' (''gefaserter Raum'') appeared for the first time in a paper by Herbert Seifert in 1933, but his definitions are limited to a very special case. The main difference from the present day conception of a fiber space, however, was that for Seifert what is now called the base space (topological space) of a fiber (topological) space ''E'' was not part of the structure, but derived from it as a quotient space of ''E''. The first definition of fiber space was given by Hassler Whitney in 1935 under the name sphere space, but in 1940 Whitney changed the name to sphere bundle.

The theory of fibered spaces, of which vector bundles, principal bundles, topological fibrations and fibered manifolds are a special case, is attributed to Herbert Seifert, Heinz Hopf, Jacques Feldbau, Whitney, Norman Steenrod, Charles Ehresmann, Jean-Pierre Serre, and others.

Fiber bundles became their own object of study in the period 1935–1940. The first general definition appeared in the works of Whitney.

Whitney came to the general definition of a fiber bundle from his study of a more particular notion of a sphere bundle, that is a fiber bundle whose fiber is a sphere of arbitrary dimension.

Formal definition

A fiber bundle is a structure $(E,\, B,\, \pi,\, F),$ where $E, B,$ and $F$ are topological spaces and $\pi : E \to B$ is a continuous surjection satisfying a ''local triviality'' condition outlined below. The space $B$ is called the of the bundle, $E$ the , and $F$ the . The map $\pi$ is called the (or ). We shall assume in what follows that the base space $B$ is connected.

We require that for every $x \in B$, there is an open neighborhood $U \subseteq B$ of $x$ (which will be called a trivializing neighborhood) such that there is a homeomorphism $\varphi : \pi^(U) \to U \times F$ (where $\pi^(U)$ is given the subspace topology, and $U \times F$ is the product space) in such a way that $\pi$ agrees with the projection onto the first factor. That is, the following diagram should commute:

where $\operatorname_1 : U \times F \to U$ is the natural projection and $\varphi : \pi^(U) \to U \times F$ is a homeomorphism. The set of all $\left\$ is called a of the bundle.

Thus for any $p \in B$, the preimage $\pi^(\)$ is homeomorphic to $F$ (since this is true of $\operatorname_1^(\)$) and is called the fiber over $p$. Every fiber bundle $\pi : E \to B$ is an open map, since projections of products are open maps. Therefore $B$ carries the quotient topology determined by the map $\pi.$

A fiber bundle $(E,\, B,\, \pi,\, F)$ is often denoted
$\begin \\ F \longrightarrow E\ \xrightarrow\ B \\ \end$
that, in analogy with a short exact sequence, indicates which space is the fiber, total space and base space, as well as the map from total to base space.

A is a fiber bundle in the category of smooth manifolds. That is, $E$, $B$, and $F$ are required to be smooth manifolds and all the functions above are required to be smooth maps.

Examples

Trivial bundle

Let $E = B \times F$ and let $\pi : E \to B$ be the projection onto the first factor. Then $\pi$ is a fiber bundle (of $F$) over $B.$ Here $E$ is not just locally a product but ''globally'' one. Any such fiber bundle is called a . Any fiber bundle over a contractible CW-complex is trivial.

Nontrivial bundles

Möbius strip

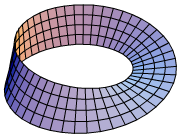
Perhaps the simplest example of a nontrivial bundle $E$ is the Möbius strip. It has the circle that runs lengthwise along the center of the strip as a base $B$ and a line segment for the fiber $F$, so the Möbius strip is a bundle of the line segment over the circle. A neighborhood $U$ of $\pi(x) \in B$ (where $x \in E$) is an arc; in the picture, this is the length of one of the squares. The preimage $\pi^(U)$ in the picture is a (somewhat twisted) slice of the strip four squares wide and one long (i.e. all the points that project to $U$).

A homeomorphism ($\varphi$ in ) exists that maps the preimage of $U$ (the trivializing neighborhood) to a slice of a cylinder: curved, but not twisted. This pair locally trivializes the strip. The corresponding trivial bundle $B\times F$ would be a cylinder, but the Möbius strip has an overall "twist". This twist is visible only globally; locally the Möbius strip and the cylinder are identical (making a single vertical cut in either gives the same space).

Klein bottle

A similar nontrivial bundle is the Klein bottle, which can be viewed as a "twisted" circle bundle over another circle. The corresponding non-twisted (trivial) bundle is the 2-torus, $S^1 \times S^1$.

Covering map

A covering space is a fiber bundle such that the bundle projection is a local homeomorphism. It follows that the fiber is a discrete space.

Vector and principal bundles

A special class of fiber bundles, called vector bundles, are those whose fibers are vector spaces (to qualify as a vector bundle the structure group of the bundle — see below — must be a linear group). Important examples of vector bundles include the tangent bundle and cotangent bundle of a smooth manifold. From any vector bundle, one can construct the frame bundle of bases, which is a principal bundle (see below).

Another special class of fiber bundles, called principal bundles, are bundles on whose fibers a free and transitive action by a group $G$ is given, so that each fiber is a principal homogeneous space. The bundle is often specified along with the group by referring to it as a principal $G$-bundle. The group $G$ is also the structure group of the bundle. Given a representation $\rho$ of $G$ on a vector space $V$, a vector bundle with $\rho(G) \subseteq \text(V)$ as a structure group may be constructed, known as the associated bundle.

Sphere bundles

A sphere bundle is a fiber bundle whose fiber is an ''n''-sphere. Given a vector bundle $E$ with a metric (such as the tangent bundle to a Riemannian manifold) one can construct the associated unit sphere bundle, for which the fiber over a point $x$ is the set of all unit vectors in $E_x$. When the vector bundle in question is the tangent bundle $TM$, the unit sphere bundle is known as the unit tangent bundle.

A sphere bundle is partially characterized by its Euler class, which is a degree $n + 1$ cohomology class in the total space of the bundle. In the case $n = 1$ the sphere bundle is called a circle bundle and the Euler class is equal to the first Chern class, which characterizes the topology of the bundle completely. For any $n$, given the Euler class of a bundle, one can calculate its cohomology using a long exact sequence called the Gysin sequence.

Mapping tori

If $X$ is a topological space and $f : X \to X$ is a homeomorphism then the mapping torus $M_f$ has a natural structure of a fiber bundle over the circle with fiber $X.$ Mapping tori of homeomorphisms of surfaces are of particular importance in 3-manifold topology.

Quotient spaces

If $G$ is a topological group and $H$ is a closed subgroup, then under some circumstances, the quotient space $G/H$ together with the quotient map $\pi : G \to G/H$ is a fiber bundle, whose fiber is the topological space $H$. A necessary and sufficient condition for ($G,\, G/H,\, \pi,\, H$) to form a fiber bundle is that the mapping $\pi$ admits local cross-sections .

The most general conditions under which the quotient map will admit local cross-sections are not known, although if $G$ is a Lie group and $H$ a closed subgroup (and thus a Lie subgroup by Cartan's theorem), then the quotient map is a fiber bundle. One example of this is the Hopf fibration, $S^3 \to S^2$, which is a fiber bundle over the sphere $S^2$ whose total space is $S^3$. From the perspective of Lie groups, $S^3$ can be identified with the special unitary group $SU(2)$. The abelian subgroup of diagonal matrices is isomorphic to the circle group $U(1)$, and the quotient $SU(2)/U(1)$ is diffeomorphic to the sphere.

More generally, if $G$ is any topological group and $H$ a closed subgroup that also happens to be a Lie group, then $G \to G/H$ is a fiber bundle.

Sections

A (or cross section) of a fiber bundle $\pi$ is a continuous map $f : B \to E$ such that $\pi(f(x)) = x$ for all ''x'' in ''B''. Since bundles do not in general have globally defined sections, one of the purposes of the theory is to account for their existence. The obstruction to the existence of a section can often be measured by a cohomology class, which leads to the theory of characteristic classes in algebraic topology.

The most well-known example is the hairy ball theorem, where the Euler class is the obstruction to the tangent bundle of the 2-sphere having a nowhere vanishing section.

Often one would like to define sections only locally (especially when global sections do not exist). A local section of a fiber bundle is a continuous map $f : U \to E$ where ''U'' is an open set in ''B'' and $\pi(f(x)) = x$ for all ''x'' in ''U''. If $(U,\, \varphi)$ is a local trivialization chart then local sections always exist over ''U''. Such sections are in 1-1 correspondence with continuous maps $U \to F$. Sections form a sheaf.

Structure groups and transition functions

Fiber bundles often come with a group of symmetries that describe the matching conditions between overlapping local trivialization charts. Specifically, let ''G'' be a topological group that acts continuously on the fiber space ''F'' on the left. We lose nothing if we require ''G'' to act faithfully on ''F'' so that it may be thought of as a group of homeomorphisms of ''F''. A ''G''-atlas for the bundle $(E, B, \pi, F)$ is a set of local trivialization charts $\$ such that for any $\varphi_i,\varphi_j$ for the overlapping charts $(U_i,\, \varphi_i)$ and $(U_j,\, \varphi_j)$ the function
$\varphi_i\varphi_j^ : \left(U_i \cap U_j\right) \times F \to \left(U_i \cap U_j\right) \times F$
is given by
$\varphi_i\varphi_j^(x,\, \xi) = \left(x,\, t_(x)\xi\right)$
where $t_ : U_i \cap U_j \to G$ is a continuous map called a . Two ''G''-atlases are equivalent if their union is also a ''G''-atlas. A ''G''-bundle is a fiber bundle with an equivalence class of ''G''-atlases. The group ''G'' is called the of the bundle; the analogous term in physics is gauge group.

In the smooth category, a ''G''-bundle is a smooth fiber bundle where ''G'' is a Lie group and the corresponding action on ''F'' is smooth and the transition functions are all smooth maps.

The transition functions $t_$ satisfy the following conditions
# $t_(x) = 1\,$
# $t_(x) = t_(x)^\,$
# $t_(x) = t_(x)t_(x).\,$

The third condition applies on triple overlaps ''U_i'' ∩ ''U_j'' ∩ ''U_k'' and is called the cocycle condition (see Čech cohomology). The importance of this is that the transition functions determine the fiber bundle (if one assumes the Čech cocycle condition).

A principal ''G''-bundle is a ''G''-bundle where the fiber ''F'' is a principal homogeneous space for the left action of ''G'' itself (equivalently, one can specify that the action of ''G'' on the fiber ''F'' is free and transitive, i.e. regular). In this case, it is often a matter of convenience to identify ''F'' with ''G'' and so obtain a (right) action of ''G'' on the principal bundle.

Bundle maps

It is useful to have notions of a mapping between two fiber bundles. Suppose that $M$ and $N$ are base spaces, and $\pi_E : E \to M$ and $\pi_F : F \to N$ are fiber bundles over $M$ and $N$, respectively. A or consists of a pair of continuous functions
$\varphi : E \to F,\quad f : M \to N$
such that $\pi_F\circ \varphi = f \circ \pi_E$. That is, the following diagram is commutative:

For fiber bundles with structure group $G$ and whose total spaces are (right) $G$-spaces (such as a principal bundle), bundle morphisms are also required to be $G$-equivariant on the fibers. This means that $\varphi : E \to F$ is also $G$-morphism from one $G$-space to another, that is, $\varphi(xs) = \varphi(x)s$ for all $x \in E$ and $s \in G$.

In case the base spaces $M$ and $N$ coincide, then a bundle morphism over $M$ from the fiber bundle $\pi_E : E \to M$ to $\pi_F : F \to M$ is a map $\varphi : E \to F$ such that $\pi_E = \pi_F \circ \varphi$. This means that the bundle map $\varphi : E \to F$ covers the identity of $M$. That is, $f \equiv \mathrm_$ and the following diagram commutes:

Assume that both $\pi_E : E \to M$ and $\pi_F : F \to M$ are defined over the same base space $M$. A bundle isomorphism is a bundle map $(\varphi,\, f)$ between $\pi_E : E \to M$ and $\pi_F : F \to M$ such that $f \equiv \mathrm_M$ and such that $\varphi$ is also a homeomorphism.Or is, at least, invertible in the appropriate category; e.g., a diffeomorphism.

Differentiable fiber bundles

In the category of differentiable manifolds, fiber bundles arise naturally as submersions of one manifold to another. Not every (differentiable) submersion $f : M \to N$ from a differentiable manifold ''M'' to another differentiable manifold ''N'' gives rise to a differentiable fiber bundle. For one thing, the map must be surjective, and $(M, N, f)$ is called a fibered manifold. However, this necessary condition is not quite sufficient, and there are a variety of sufficient conditions in common use.

If ''M'' and ''N'' are compact and connected, then any submersion $f : M \to N$ gives rise to a fiber bundle in the sense that there is a fiber space ''F'' diffeomorphic to each of the fibers such that $(E, B, \pi, F) = (M, N, f, F)$ is a fiber bundle. (Surjectivity of $f$ follows by the assumptions already given in this case.) More generally, the assumption of compactness can be relaxed if the submersion $f : M \to N$ is assumed to be a surjective proper map, meaning that $f^(K)$ is compact for every compact subset ''K'' of ''N''. Another sufficient condition, due to , is that if $f : M \to N$ is a surjective submersion with ''M'' and ''N'' differentiable manifolds such that the preimage $f^\$ is compact and connected for all $x \in N,$ then $f$ admits a compatible fiber bundle structure .

Generalizations

* The notion of a bundle applies to many more categories in mathematics, at the expense of appropriately modifying the local triviality condition; cf. principal homogeneous space and torsor (algebraic geometry).
* In topology, a fibration is a mapping $\pi : E \to B$ that has certain homotopy-theoretic properties in common with fiber bundles. Specifically, under mild technical assumptions a fiber bundle always has the homotopy lifting property or homotopy covering property (see for details). This is the defining property of a fibration.
* A section of a fiber bundle is a "function whose output range is continuously dependent on the input." This property is formally captured in the notion of dependent type.

See also

* Affine bundle
* Algebra bundle
* Characteristic class
* Covering map
* Equivariant bundle
* Fibered manifold
* Fibration
* Gauge theory
* Hopf bundle
* I-bundle
* Natural bundle
* Principal bundle
* Projective bundle
* Pullback bundle
* Quasifibration
* Universal bundle
* Vector bundle
* Wu–Yang dictionary

Notes

References

*
*
*
*
*
*
*

External links

Fiber Bundle
PlanetMath
*


* Sardanashvily, Gennadi, Fibre bundles, jet manifolds and Lagrangian theory. Lectures for theoreticians,

{{DEFAULTSORT:Fiber Bundle