B+ tree

A B+ tree is an m-ary tree with a variable but often large number of children per node. A B+ tree consists of a root, internal nodes and leaves. The root may be either a leaf or a node with two or more children.

A B+ tree can be viewed as a B-tree in which each node contains only keys (not key–value pairs), and to which an additional level is added at the bottom with linked leaves.

The primary value of a B+ tree is in storing data for efficient retrieval in a block-oriented storage context—in particular, filesystems. This is primarily because unlike binary search trees, B+ trees have very high fanout (number of pointers to child nodes in a node, typically on the order of 100 or more), which reduces the number of I/O operations required to find an element in the tree.

History

There is no single paper introducing the B+ tree concept. Instead, the notion of maintaining all data in leaf nodes is repeatedly brought up as an interesting variant of the B-tree, which was introduced by R. Bayer and E. McCreight. Douglas Comer notes in an early survey of B-trees (which also covers B+ trees) that the B+ tree was used in IBM's VSAM data access software, and refers to an IBM published article from 1973.

Structure

Pointer structure

As with other trees, B+ trees can be represented as a collection of three types of nodes: ''root'', ''internal'' (a.k.a. interior), and ''leaf''. In B+ trees, the following properties are maintained for these nodes:

* If $k_i$ exists in any node in a B+ tree, then exists in that node where $i \ge 1$.
* All leaf nodes have the same number of ancestors (i.e., they are all at the same depth).

The pointer properties of nodes are summarized in the tables below:

* : Maximum number of potential search keys for each node in a B+ tree. (this value is constant over the entire tree).
* : The pointer at the zero-based node index .
* : The search key at the zero-based node index .

Node bounds

The node bounds are summarized in the table below:

Intervals in internal nodes

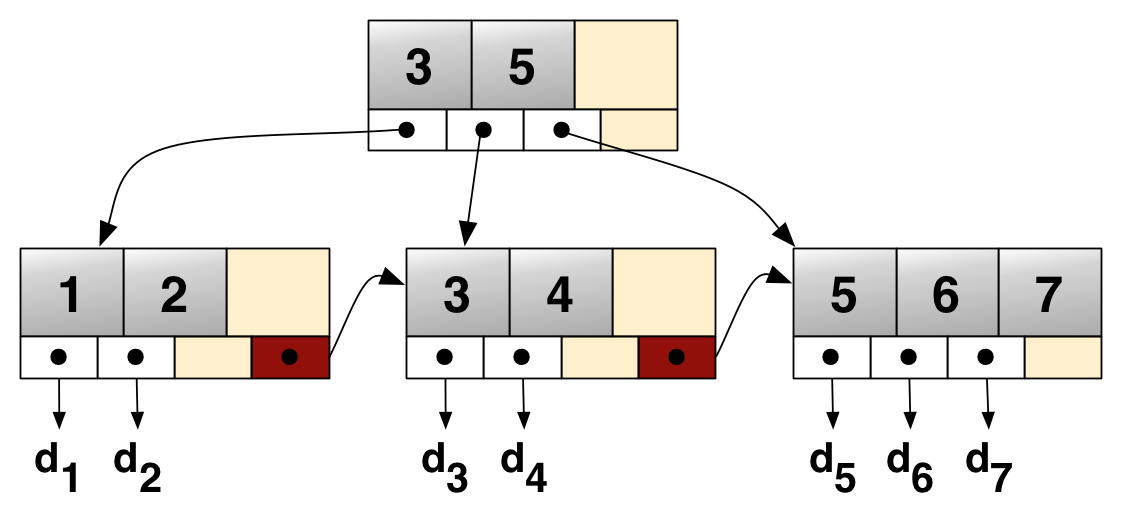
By definition, each value contained within the B+ tree is a key contained in exactly one leaf node. Each key is required to be directly comparable with every other key, which forms a total order. This enables each leaf node to keep all of its keys sorted at all times, which then enables each internal node to construct an ordered collection of intervals representing the contiguous extent of values contained in a given leaf. Internal nodes higher in the tree can then construct their own intervals, which recursively aggregate the intervals contained in their own child internal nodes. Eventually, the root of a B+ Tree represents the whole range of values in the tree, where every internal node represents a subinterval.

For this recursive interval information to be retained, internal nodes must additionally contain $m - 1$ copies of keys $l_i$ for i \in , m - 1/math> representing the least element within the interval covered by the child with index (which may itself be an internal node, or a leaf). Where represents the ''actual'' number of children for a given internal node.

Characteristics

The ''order'' or ''branching factor'' of a B+ tree measures the capacity of interior nodes, i.e. their maximum allowed number of direct child nodes. This value is constant over the entire tree. For a -order B+ tree with levels of index:
* The maximum number of records stored is $n_ = b^h - b^$
* The minimum number of records stored is $n_ = 2\left\lceil\tfrac\right\rceil^-2\left\lceil\tfrac\right\rceil^$
* The minimum number of keys is $n_\mathrm = 2\left\lceil\tfrac\right\rceil^-1$
* The maximum number of keys is $n_\mathrm = b^h-1$
* The space required to store the tree is $O(n)$
* Inserting a record requires $O(\log_bn)$ operations
* Finding a record requires $O(\log_bn)$ operations
* Removing a (previously located) record requires $O(\log_bn)$ operations
* Performing a range query with ''k'' elements occurring within the range requires $O(\log_bn+k)$ operations
* The B+ tree structure expands/contracts as the number of records increases/decreases. There are no restrictions on the size of B+ trees. Thus, increasing usability of a database system.
* Any change in structure does not affect performance due to balanced tree properties.
* The data is stored in the leaf nodes and more branching of internal nodes helps to reduce the tree's height, thus, reduce search time. As a result, it works well in secondary storage devices.
* Searching becomes extremely simple because all records are stored only in the leaf node and are sorted sequentially in the linked list.
* We can retrieve range retrieval or partial retrieval using B+ tree. This is made easier and faster by traversing the tree structure. This feature makes B+ tree structure applied in many search methods.

Algorithms

Search

We are looking for a value in the B+ Tree. This means that starting from the root, we are looking for the leaf which may contain the value . At each node, we figure out which internal node we should follow. An internal B+ Tree node has at most $m \le b$ children, where every one of them represents a different sub-interval. We select the corresponding child via a linear search of the entries, then when we finally get to a leaf, we do a linear search of its elements for the desired key. Because we only traverse one branch of all the children at each rung of the tree, we achieve $O(\log N)$ runtime, where is the total number of keys stored in the leaves of the B+ tree.

function search(''k'', ''root'') is
let leaf = leaf_search(k, root)
for leaf_key in leaf.keys():
if k = leaf_key:
return true
return false

function leaf_search(''k'', ''node'') is
if node is a leaf:
return node
let p = node.children()
let l = node.left_sided_intervals()
assert $, p, = , l, + 1$
let m = p.len()
for i from 1 to m - 1:
if k \le l /math>:
return leaf_search(k, p
return leaf_search(k, p

Note that this pseudocode uses 1-based array indexing.

Insertion

* Perform a search to determine which node the new record should go into.
* If the node is not full (at most $b - 1$ entries after the insertion), add the record.
* Otherwise, ''before'' inserting the new record
** Split the node.
*** original node has $\lceil (K+1)/2 \rceil$ items
*** new node has $\lfloor (K+1)/2 \rfloor$ items
** Copy $\lceil (K+1)/2 \rceil$-th key to the parent, and insert the new node to the parent.
** Repeat until a parent is found that need not split.
** Insert the new record into the new node.
* If the root splits, treat it as if it has an empty parent and split as outlined above.
B+ trees grow at the root and not at the leaves.

Bulk-loading

Given a collection of data records, we want to create a B+ tree index on some key field. One approach is to insert each record into an empty tree. However, it is quite expensive, because each entry requires us to start from the root and go down to the appropriate leaf page. An efficient alternative is to use bulk-loading.
* The first step is to sort the data entries according to a search key in ascending order.
* We allocate an empty page to serve as the root, and insert a pointer to the first page of entries into it.
* When the root is full, we split the root, and create a new root page.
* Keep inserting entries to the right most index page just above the leaf level, until all entries are indexed.

Note:
* when the right-most index page above the leaf level fills up, it is split;
* this action may, in turn, cause a split of the right-most index page one step closer to the root;
* splits only occur on the right-most path from the root to the leaf level.

Deletion

The purpose of the delete algorithm is to remove the desired entry node from the tree structure. We recursively call the delete algorithm on the appropriate node until no node is found. For each function call, we traverse along, using the index to navigate until we find the node, remove it, and then work back up to the root.

At entry L that we wish to remove:
* If L is at least half-full, done
* If L has only d-1 entries, try to re-distribute, borrowing from sibling (adjacent node with same parent as L).After the re-distribution of two sibling nodes happens, the parent node must be updated to reflect this change. The index key that points to the second sibling must take the smallest value of that node to be the index key.
* If re-distribute fails, merge L and sibling. After merging, the parent node is updated by deleting the index key that point to the deleted entry. In other words, if merge occurred, must delete entry (pointing to L or sibling) from parent of L.

Note: merge could propagate to root, which means decreasing height.

Implementation

The leaves (the bottom-most index blocks) of the B+ tree are often linked to one another in a linked list; this makes range queries or an (ordered) iteration through the blocks simpler and more efficient (though the aforementioned upper bound can be achieved even without this addition). This does not substantially increase space consumption or maintenance on the tree. This illustrates one of the significant advantages of a B+tree over a B-tree; in a B-tree, since not all keys are present in the leaves, such an ordered linked list cannot be constructed. A B+tree is thus particularly useful as a database system index, where the data typically resides on disk, as it allows the B+tree to actually provide an efficient structure for housing the data itself (this is described in as index structure "Alternative 1").

If a storage system has a block size of B bytes, and the keys to be stored have a size of k, arguably the most efficient B+ tree is one where $b=\tfrac B k -1$. Although theoretically the one-off is unnecessary, in practice there is often a little extra space taken up by the index blocks (for example, the linked list references in the leaf blocks). Having an index block which is slightly larger than the storage system's actual block represents a significant performance decrease; therefore erring on the side of caution is preferable.

If nodes of the B+ tree are organized as arrays of elements, then it may take a considerable time to insert or delete an element as half of the array will need to be shifted on average. To overcome this problem, elements inside a node can be organized in a binary tree or a B+ tree instead of an array.

B+ trees can also be used for data stored in RAM. In this case a reasonable choice for block size would be the size of processor's cache line.

Space efficiency of B+ trees can be improved by using some compression techniques. One possibility is to use delta encoding to compress keys stored into each block. For internal blocks, space saving can be achieved by either compressing keys or pointers. For string keys, space can be saved by using the following technique: Normally the ''i''-th entry of an internal block contains the first key of block . Instead of storing the full key, we could store the shortest prefix of the first key of block that is strictly greater (in lexicographic order) than last key of block ''i''. There is also a simple way to compress pointers: if we suppose that some consecutive blocks are stored contiguously, then it will suffice to store only a pointer to the first block and the count of consecutive blocks.

All the above compression techniques have some drawbacks. First, a full block must be decompressed to extract a single element. One technique to overcome this problem is to divide each block into sub-blocks and compress them separately. In this case searching or inserting an element will only need to decompress or compress a sub-block instead of a full block. Another drawback of compression techniques is that the number of stored elements may vary considerably from a block to another depending on how well the elements are compressed inside each block.

Applications

File systems

The ReiserFS, NSS, XFS, JFS, ReFS, and BFS filesystems all use this type of tree for metadata indexing; BFS also uses B+ trees for storing directories. NTFS uses B+ trees for directory and security-related metadata indexing. EXT4 uses extent trees (a modified B+ tree data structure) for file extent indexing. APFS uses B+ trees to store mappings from filesystem object IDs to their locations on disk, and to store filesystem records (including directories), though these trees' leaf nodes lack sibling pointers.

Database systems

Relational database management systems such as IBM Db2, Informix, Microsoft SQL Server, Oracle 8, Sybase ASE, and SQLiteSQLite Version 3 Overview
/ref> support this type of tree for table indices, though each such system implements the basic B+ tree structure with variations and extensions. Many NoSQL database management systems such as CouchDBCouchDB Guide
/ref> and Tokyo CabinetTokyo Cabinet reference
also support this type of tree for data access and storage.

Finding objects in a high-dimensional database that are comparable to a particular query object is one of the most often utilized and yet expensive procedures in such systems. In such situations, finding the closest neighbor using a B+ tree is productive.

iDistance

B+ tree is efficiently used to construct an indexed search method called iDistance. iDistance searches for k nearest neighbors (kNN) in high-dimension metric spaces. The data in those high-dimension spaces is divided based on space or partition strategies, and each partition has an index value that is close with the respect to the partition. From here, those points can be efficiently implemented using B+ tree, thus, the queries are mapped to single dimensions ranged search. In other words, the iDistance technique can be viewed as a way of accelerating the sequential scan. Instead of scanning records from the beginning to the end of the data file, the iDistance starts the scan from spots where the nearest neighbors can be obtained early with a very high probability.

NVRAM

Nonvolatile random-access memory (NVRAM) has been using B+ tree structure as the main memory access technique for the Internet Of Things (IoT) system because of its non static power consumption and high solidity of cell memory.  B+ can regulate the trafficking of data to memory efficiently. Moreover, with advanced strategies on frequencies of some highly used leaf or reference point, the B+ tree shows significant results in increasing the endurance of database systems.

See also

* Binary search tree
* B-tree
* Divide-and-conquer algorithm

Notes

References

External links

B+ tree in Python, used to implement a list



Evaluating the performance of CSB+-trees on Mutithreaded Architectures

Effect of node size on the performance of cache conscious B+-trees

Fractal Prefetching B+-trees

Towards pB+-trees in the field: implementations Choices and performance

Cache-Conscious Index Structures for Main-Memory Databases







B +-trees by Kerttu Pollari-Malmi

Data Structures B-Trees and B+ Trees

Implementations

Memory based B+ tree implementation as C++ template library

2019 improvement of previous

Stream based B+ tree implementation as C++ template library

Open Source JavaScript B+ Tree Implementation

Perl implementation of B+ trees

Java/C#/Python implementations of B+ treesC# B+ tree and related "A-List" data structures

File based B+Tree in C# with threading and MVCC support

Fast semi-persistent in-memory B+ Tree in TypeScript/JavaScript, MIT License

JavaScript B+ Tree, MIT License

JavaScript B+ Tree, Interactive and Open Source

{{DEFAULTSORT:B plus Tree
B-tree
1972 in computing
Computer-related introductions in 1972