attenuator (electronics)

An attenuator is a passive broadband electronic device that reduces the power of a signal without appreciably distorting its waveform.

An attenuator is effectively the opposite of an amplifier, though the two work by different methods. While an amplifier provides gain, an attenuator provides loss, or gain less than unity. An attenuator is often referred to as a "pad" in audio electronics.

Construction and usage

Attenuators are usually passive devices made from simple voltage divider networks. Switching between different resistances forms adjustable stepped attenuators and continuously adjustable ones using potentiometers. For higher frequencies precisely matched low voltage standing wave ratio (VSWR) resistance networks are used.

Fixed attenuators in circuits are used to lower voltage, dissipate power, and to improve impedance matching. In measuring signals, attenuator pads or adapters are used to lower the amplitude of the signal a known amount to enable measurements, or to protect the measuring device from signal levels that might damage it. Attenuators are also used to 'match' impedance by lowering apparent SWR (Standing Wave Ratio).

Attenuator circuits

Basic circuits used in attenuators are pi (Π) pads (π-type) and T pads. These may be required to be balanced or unbalanced networks depending on whether the line geometry with which they are to be used is balanced or unbalanced. For instance, attenuators used with coaxial lines would be the unbalanced form while attenuators for use with twisted pair are required to be the balanced form.

Four fundamental attenuator circuit diagrams are given in the figures on the left. Since an attenuator circuit consists solely of passive resistor elements, it is both linear and reciprocal. If the circuit is also made symmetrical (this is usually the case since it is usually required that the input and output impedance Z₁ and Z₂ are equal), then the input and output ports are not distinguished, but by convention the left and right sides of the circuits are referred to as input and output, respectively.

Various tables and calculators are available that provide a means of determining the appropriate resistor values for achieving particular loss values, such as that published by the NAB in 1960 for losses ranging from 1/2 to 40 dB, for use in 600 ohm circuits.

Attenuator characteristics

Key specifications for attenuators are:
* Attenuation expressed in decibels of relative power. A 3 dB pad reduces power to one half, 6 dB to one fourth, 10 dB to one tenth, 20 dB to one hundredth, 30 dB to one thousandth and so on. When input and output impedances are the same, voltage attenuation will be the square root of power attenuation, so, for example, a 6 dB attenuator that reduces power to one fourth will reduce the voltage (and the current) by half.
* Nominal impedance, for example 50 ohm
* Frequency bandwidth, for example DC-18 GHz
* Power dissipation depends on mass and surface area of resistance material as well as possible additional cooling fins.
* SWR is the standing wave ratio for input and output ports
* Accuracy
* Repeatability

RF attenuators

Radio frequency attenuators are typically coaxial in structure with precision connectors as ports and coaxial, micro strip or thin-film internal structure. Above SHF special waveguide structure is required. The flap attenuator is designed for use in waveguides to attenuate the signal.

Important characteristics are:
*accuracy,
*low SWR,
*flat frequency-response and
*repeatability.

The size and shape of the attenuator depends on its ability to dissipate power. RF attenuators are used as loads for and as known attenuation and protective dissipation of power in measuring RF signals.About RF attenuators
– Herley General Microwave

Audio attenuators

A line-level attenuator in the preamp or a power attenuator after the power amplifier uses electrical resistance to reduce the amplitude of the signal that reaches the speaker, reducing the volume of the output. A line-level attenuator has lower power handling, such as a 1/2-watt potentiometer or voltage divider and controls preamp level signals, whereas a power attenuator has higher power handling capability, such as 10 watts or more, and is used between the power amplifier and the speaker.

* Power attenuator (guitar)
* Guitar amplifier

Component values for resistive pads and attenuators

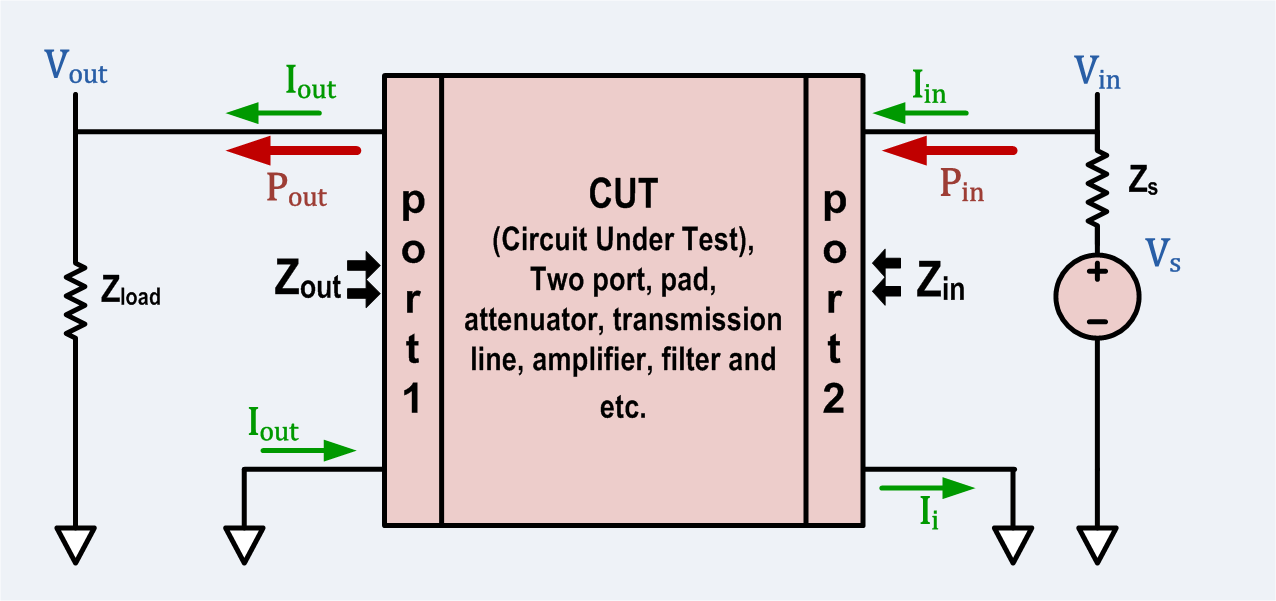
This section concerns pi-pads, T-pads and L-pads made entirely from resistors and terminated on each port with a purely real resistance.

*All impedance, currents, voltages and two-port parameters will be assumed to be purely real. For practical applications, this assumption is often close enough.
* The pad is designed for a particular load impedance, Z_Load, and a particular source impedance, Z_s.
**The impedance seen looking into the input port will be Z_S if the output port is terminated by Z_Load.
**The impedance seen looking into the output port will be Z_Load if the input port is terminated by Z_S.

Reference figures for attenuator component calculation

The attenuator two-port is generally bidirectional. However, in this section it will be treated as though it were one way. In general, either of the two figures applies, but the first figure (which depicts the source on the left) will be tacitly assumed most of the time. In the case of the L-pad, the second figure will be used if the load impedance is greater than the source impedance.

Each resistor in each type of pad discussed is given a unique designation to decrease confusion.

The L-pad component value calculation assumes that the design impedance for port 1 (on the left) is equal or higher than the design impedance for port 2.

Terms used

* Pad will include pi-pad, T-pad, L-pad, attenuator, and two-port.
* Two-port will include pi-pad, T-pad, L-pad, attenuator, and two-port.
* Input port will mean the input port of the two-port.
* Output port will mean the output port of the two-port.
* Symmetric means a case where the source and load have equal impedance.
* Loss means the ratio of power entering the input port of the pad divided by the power absorbed by the load.
* Insertion Loss means the ratio of power that would be delivered to the load if the load were directly connected to the source divided by the power absorbed by the load when connected through the pad.

Symbols used

Passive, resistive pads and attenuators are bidirectional two-ports, but in this section they will be treated as unidirectional.

*Z_S = the output impedance of the source.
*Z_Load = the input impedance of the load.
*Z_in = the impedance seen looking into the input port when Z_Load is connected to the output port. Z_in is a function of the load impedance.
*Z_out = the impedance seen looking into the output port when Z_s is connected to the input port. Z_out is a function of the source impedance.
*V_s = source open circuit or unloaded voltage.
*V_in = voltage applied to the input port by the source.
*V_out = voltage applied to the load by the output port.
*I_in = current entering the input port from the source.
*I_out = current entering the load from the output port.
*P_in = V_in I_in = power entering the input port from the source.
*P_out = V_out I_out = power absorbed by the load from the output port.
*P_direct = the power that would be absorbed by the load if the load were connected directly to the source.
*L_pad = 10 log₁₀ (P_in / P_out), always. Further, if Z_s = Z_Load, then L_pad = 20 log₁₀ (V_in / V_out ). Note, as defined, Loss ≥ 0 dB
*L_insertion = 10 log₁₀ (P_direct / P_out ). Further, if Z_s = Z_Load, then L_insertion = L_pad.
*Loss ≡ L_pad. Loss is defined to be L_pad.

Symmetric T pad resistor calculation

$A = 10^ \qquad R_a = R_b = Z_S \frac \qquad R_c = \frac$ see Valkenburg p 11-3

Symmetric pi pad resistor calculation

$A = 10^ \qquad R_x = R_y = Z_S \frac \qquad R_z = \frac$ see Valkenburg p 11-3

L-Pad for impedance matching resistor calculation

If a source and load are both resistive (i.e. Z₁ and Z₂ have zero or very small imaginary part) then a resistive L-pad can be used to match them to each other. As shown, either side of the L-pad can be the source or load, but the Z₁ side must be the side with the higher impedance.
$R_q = \frac \qquad R_p = Z_m \sqrt$
$\text = 20 \log_ \left(\sqrt + \sqrt\right) \quad \text \quad \rho = \frac \quad Z_m = \sqrt$ see

Large positive numbers means loss is large. The loss is a monotonic function of the impedance ratio. Higher ratios require higher loss.

Converting T-pad to pi-pad

This is the Y-Δ transform
$\begin R_z = \frac \\ R_x = \frac \\ R_y = \frac . \end$

Converting pi-pad to T-pad

This is the Δ-Y transform
$\begin R_c &= \frac \\ R_a &= \frac \\ R_b &= \frac \end$

Conversion between two-ports and pads

T-pad to impedance parameters

The impedance parameters for a passive two-port are
$V_1 = Z_ I_1 + Z_ I_2 \qquad V_2 = Z_ I_1 + Z_ I_2 \qquad \text \qquad Z_ = Z_$
It is always possible to represent a resistive t-pad as a two-port. The representation is particularly simple using impedance parameters as follows:
$Z_ = R_c \qquad Z_ = R_c + R_a \qquad Z_ = R_c + R_b$

Impedance parameters to T-pad

The preceding equations are trivially invertible, but if the loss is not enough, some of the t-pad components will have negative resistances.
$R_c = Z_ \qquad R_a = Z_ - Z_ \qquad R_b = Z_ - Z_$

Impedance parameters to pi-pad

These preceding T-pad parameters can be algebraically converted to pi-pad parameters.
$\begin R_z &= \frac \\ R_x &= \frac \\ R_y &= \frac \end$

Pi-pad to admittance parameters

The admittance parameters for a passive two port are
$I_1 = Y_ V_1 + Y_ V_2 \qquad I_2 = Y_ V_1 + Y_ V_2 \qquad \text \qquad Y_ = Y_$
It is always possible to represent a resistive pi pad as a two-port. The representation is particularly simple using admittance parameters as follows:
$Y_ = \frac \qquad Y_ = \frac + \frac \qquad Y_ = \frac + \frac$

Admittance parameters to pi-pad

The preceding equations are trivially invertible, but if the loss is not enough, some of the pi-pad components will have negative resistances.
$R_z = \frac \qquad R_x = \frac \qquad R_y = \frac \,$

General case, determining impedance parameters from requirements

Because the pad is entirely made from resistors, it must have a certain minimum loss to match source and load if they are not equal.

The minimum loss is given by
$\mathrm = 20 \log_ \left ( \sqrt + \sqrt \right ) \, \quad \text \quad \rho = \frac$

Although a passive matching two-port can have less loss, if it does it will not be convertible to a resistive attenuator pad.
$A = 10^ \qquad Z_ = Z_S \frac \qquad Z_ = Z_\text \frac \qquad Z_ = 2 \frac$

Once these parameters have been determined, they can be implemented as a T or pi pad as discussed above.

See also

* RF and microwave variable attenuators
* Optical attenuator

Notes

References

*
*

External links

Guitar amp power attenuator FAQBasic attenuator circuitsExplanation of attenuator types, impedance matching, and very useful calculator

{{DEFAULTSORT:Attenuator (Electronics)
Resistive components
Microwave technology
Audio engineering