Astroid2

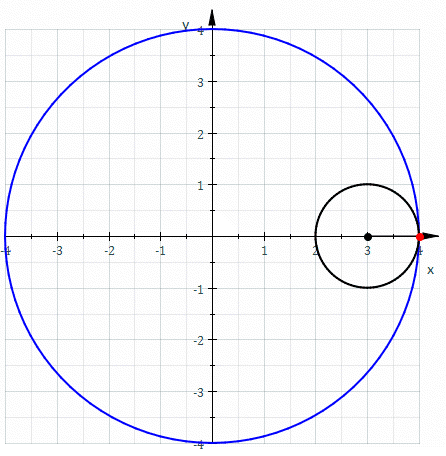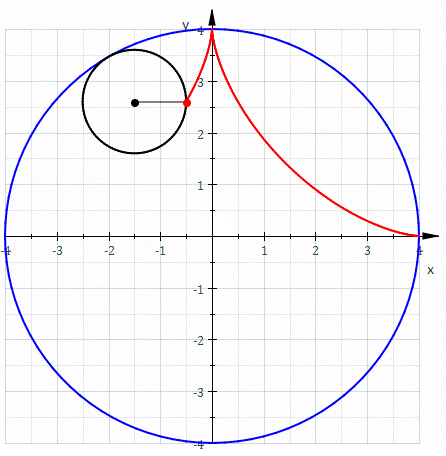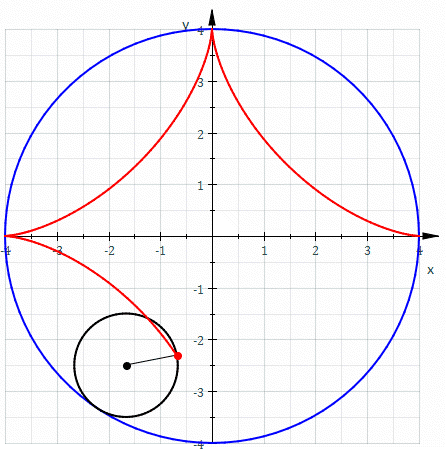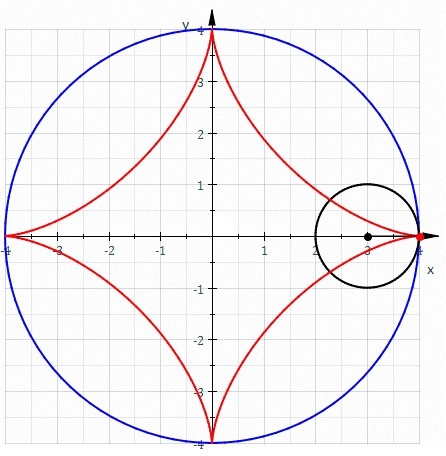
In mathematics, an astroid is a particular type of roulette curve: a hypocycloid with four cusps. Specifically, it is the locus of a point on a circle as it rolls inside a fixed circle with four times the radius. By double generation, it is also the locus of a point on a circle as it rolls inside a fixed circle with 4/3 times the radius. It can also be defined as the envelope of a line segment of fixed length that moves while keeping an end point on each of the axes. It is therefore the envelope of the moving bar in the Trammel of Archimedes.

Its modern name comes from the Greek word for "star". It was proposed, originally in the form of "Astrois", by Joseph Johann von Littrow in 1838. The curve had a variety of names, including tetracuspid (still used), cubocycloid, and paracycle. It is nearly identical in form to the evolute of an ellipse.

Equations

If the radius of the fixed circle is ''a'' then the equation is given by
$x^ + y^ = a^.$
This implies that an astroid is also a superellipse.

Parametric equations are

\begin
x = a\cos^3 t &= \frac \left( 3\cos \left(t\right) + \cos \left(3t\right)\right), \\ ex y = a\sin^3 t &= \frac \left( 3\sin \left(t\right) - \sin \left(3t\right) \right).
\end

The pedal equation with respect to the origin is
$r^2 = a^2 - 3p^2,$

the Whewell equation is
$s = \cos 2\varphi,$
and the Cesàro equation is
$R^2 + 4s^2 = \frac.$

The polar equation is
$r = \frac.$

The astroid is a real locus of a plane algebraic curve of genus zero. It has the equation
$\left(x^2 + y^2 - a^2\right)^3 + 27 a^2 x^2 y^2 = 0.$

The astroid is, therefore, a real algebraic curve of degree six.

Derivation of the polynomial equation

The polynomial equation may be derived from Leibniz's equation by elementary algebra:
$x^ + y^ = a^.$

Cube both sides:
\begin
x^ + 3x^y^ + 3x^y^ + y^ &= a^ \\ .5exx^2 + 3x^y^ \left(x^ + y^\right) + y^2 &= a^2 \\ exx^2 + y^2 - a^2 &= -3x^y^ \left(x^ + y^\right)
\end

Cube both sides again:
$\left(x^2 + y^2 - a^2\right)^3 = -27 x^2 y^2 \left(x^ + y^\right)^3$

But since:
$x^ + y^ = a^ \,$

It follows that
$\left(x^ + y^\right)^3 = a^2.$

Therefore:
$\left(x^2 + y^2 - a^2\right)^3 = -27 x^2 y^2 a^2$
or
$\left(x^2 + y^2 - a^2\right)^3 + 27 x^2 y^2 a^2 = 0.$

Metric properties

;Area enclosed :$\frac \pi a^2$
;Length of curve :$6a$
;Volume of the surface of revolution of the enclose area about the ''x''-axis. :$\frac\pi a^3$
;Area of surface of revolution about the ''x''-axis :$\frac\pi a^2$

Properties

The astroid has four cusp singularities in the real plane, the points on the star. It has two more complex cusp singularities at infinity, and four complex double points, for a total of ten singularities.

The dual curve to the astroid is the cruciform curve with equation $x^2 y^2 = x^2 + y^2.$
The evolute of an astroid is an astroid twice as large.

The astroid has only one tangent line in each oriented direction, making it an example of a hedgehog.

See also

* Cardioid – an epicycloid with one cusp
* Nephroid – an epicycloid with two cusps
* Deltoid – a hypocycloid with three cusps
* Stoner–Wohlfarth astroid – a use of this curve in magnetics
* Spirograph

References

*
*
*

External links

* {{springer, title=Astroid, id=p/a013540

"Astroid" at The MacTutor History of Mathematics archive

"Astroid" at The Encyclopedia of Remarkable Mathematical Forms





Bars of an Astroid
by Sándor Kabai, The Wolfram Demonstrations Project.

Sextic curves
Roulettes (curve)