Archimedes principle on:
[Wikipedia]
[Google]
[Amazon]
Archimedes' principle states that the upward
 A simplified explanation for the integration of the pressure over the contact area may be stated as follows:
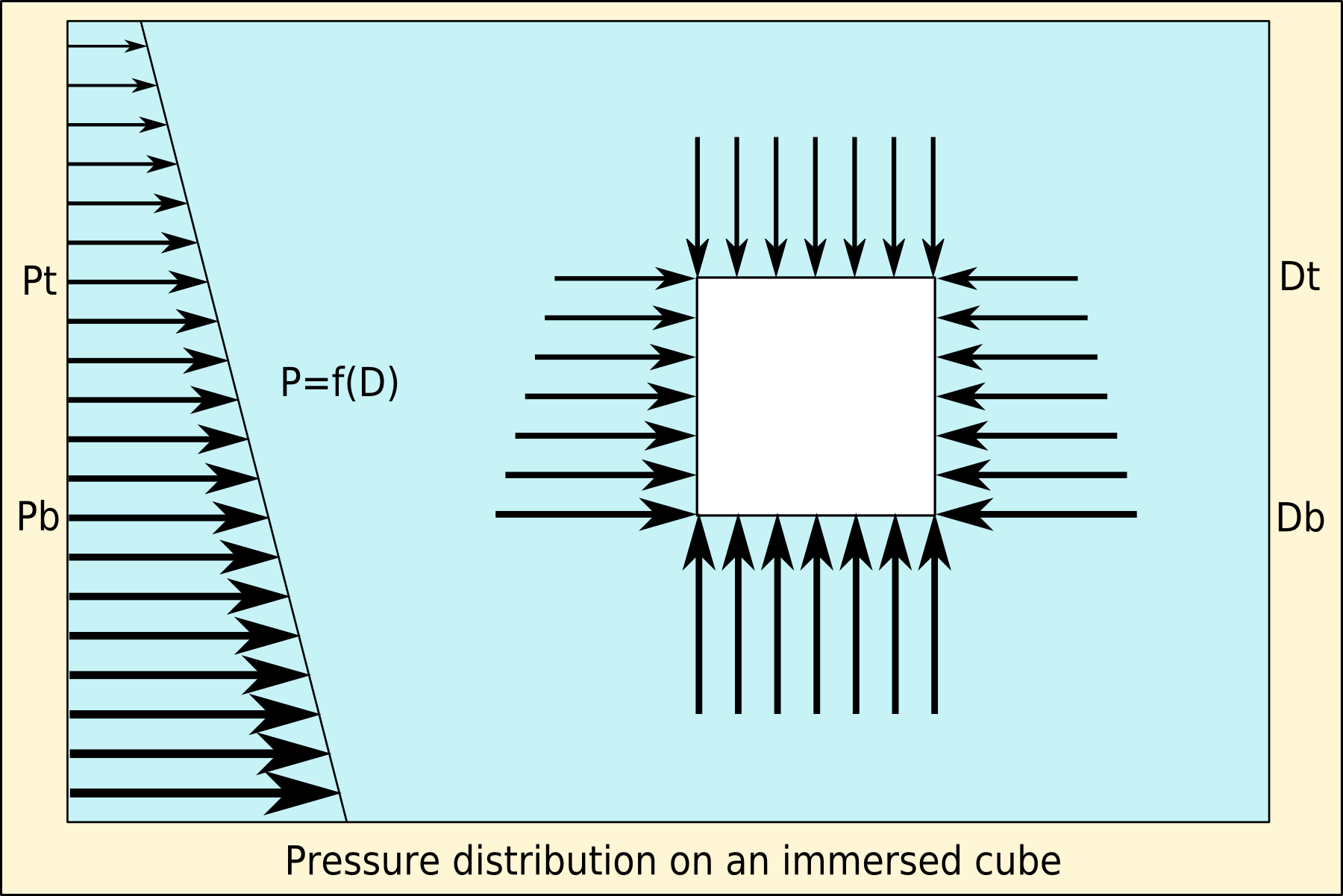
Consider a cube immersed in a fluid with the upper surface horizontal.
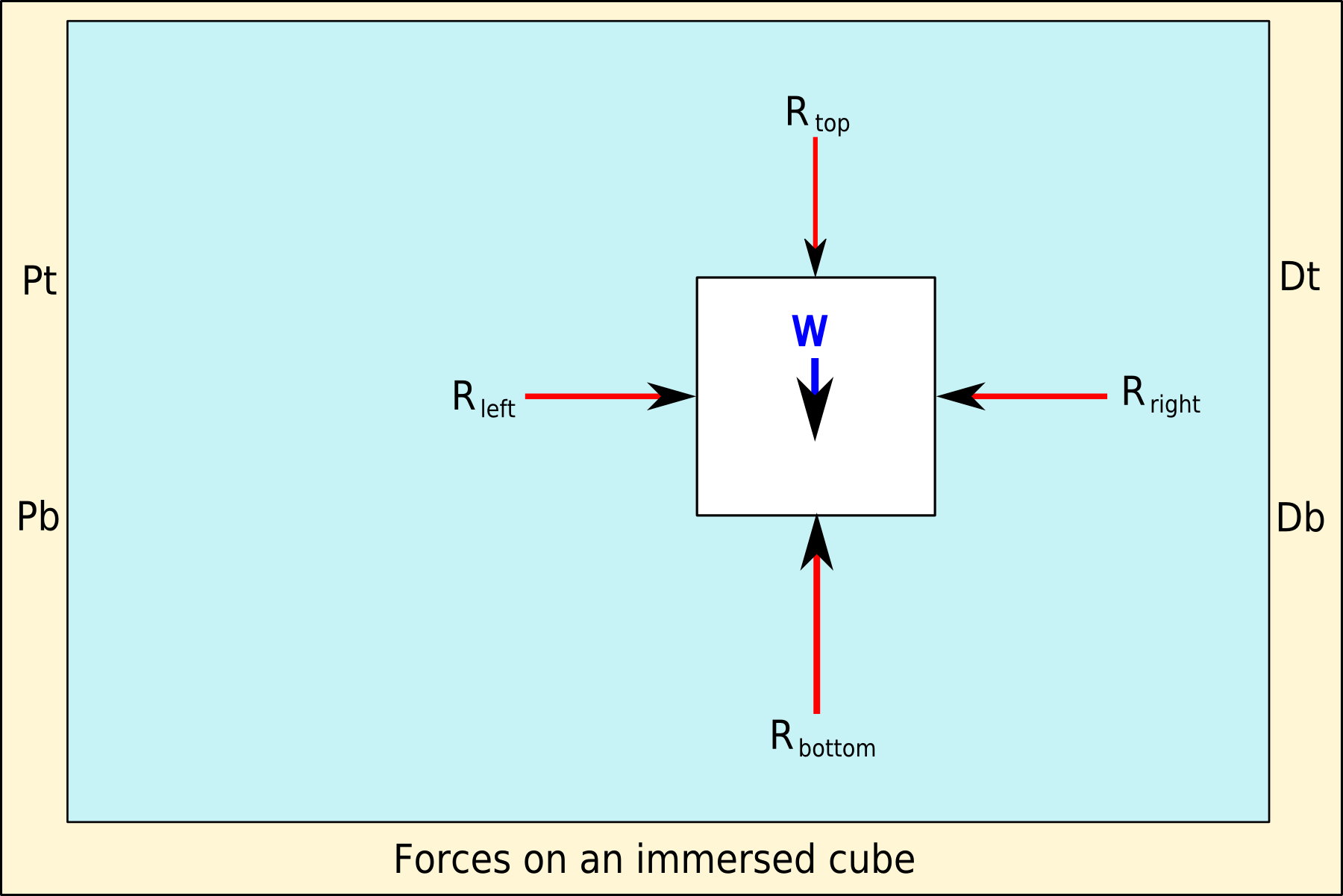
The sides are identical in area, and have the same depth distribution, therefore they also have the same pressure distribution, and consequently the same total force resulting from hydrostatic pressure, exerted perpendicular to the plane of the surface of each side.
There are two pairs of opposing sides, therefore the resultant horizontal forces balance in both orthogonal directions, and the resultant force is zero.
The upward force on the cube is the pressure on the bottom surface integrated over its area. The surface is at constant depth, so the pressure is constant. Therefore, the integral of the pressure over the area of the horizontal bottom surface of the cube is the hydrostatic pressure at that depth multiplied by the area of the bottom surface.
Similarly, the downward force on the cube is the pressure on the top surface integrated over its area. The surface is at constant depth, so the pressure is constant. Therefore, the integral of the pressure over the area of the horizontal top surface of the cube is the hydrostatic pressure at that depth multiplied by the area of the top surface.
As this is a cube, the top and bottom surfaces are identical in shape and area, and the pressure difference between the top and bottom of the cube is directly proportional to the depth difference, and the resultant force difference is exactly equal to the weight of the fluid that would occupy the volume of the cube in its absence.
This means that the resultant upward force on the cube is equal to the weight of the fluid that would fit into the volume of the cube, and the downward force on the cube is its weight, in the absence of external forces.
This analogy is valid for variations in the size of the cube.
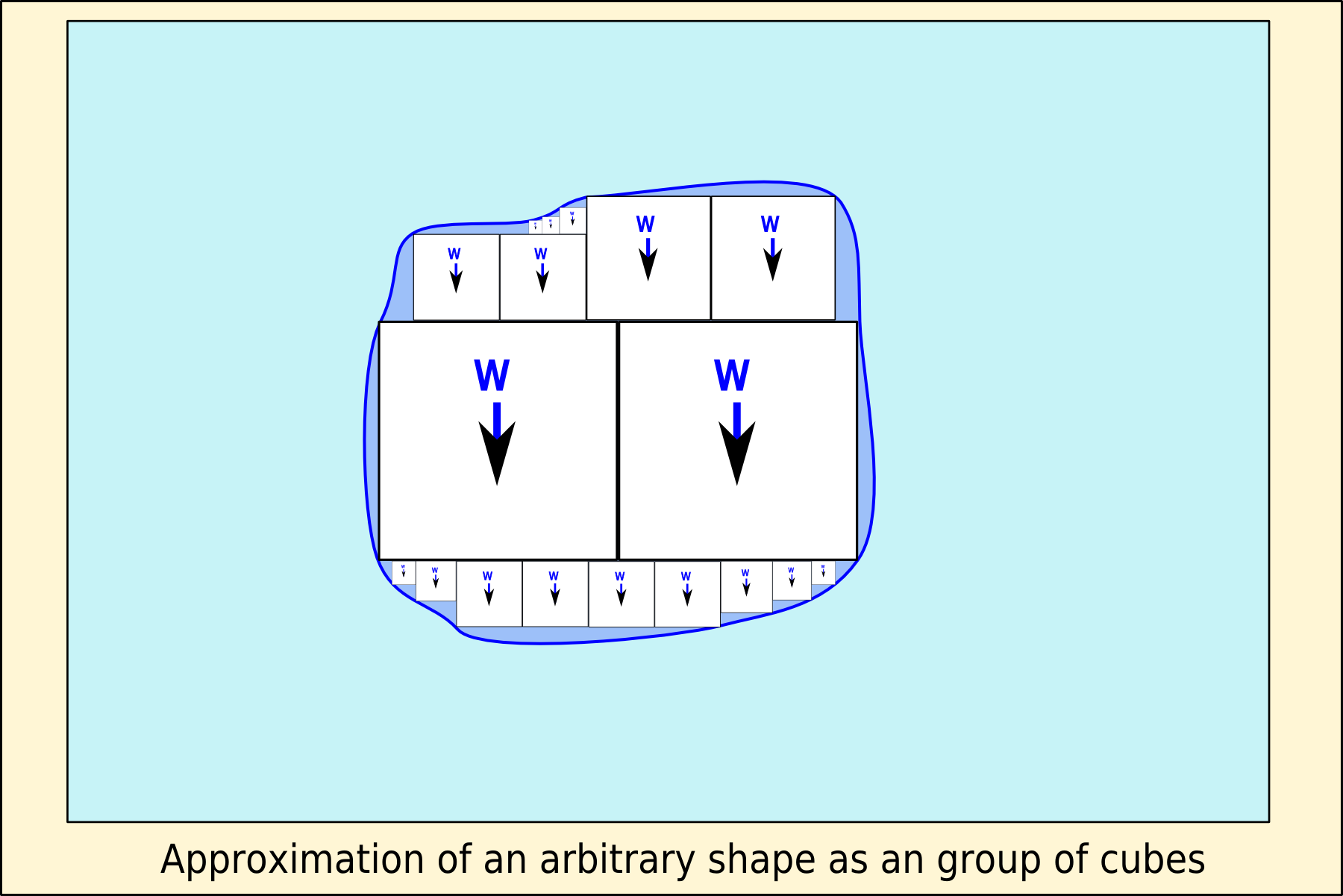
If two cubes are placed alongside each other with a face of each in contact, the pressures and resultant forces on the sides or parts thereof in contact are balanced and may be disregarded, as the contact surfaces are equal in shape, size and pressure distribution, therefore the buoyancy of two cubes in contact is the sum of the buoyancies of each cube. This analogy can be extended to an arbitrary number of cubes.
An object of any shape can be approximated as a group of cubes in contact with each other, and as the size of the cubes is decreased, the precision of the approximation increases. The limiting case for infinitely small cubes is the exact equivalence.
Angled surfaces do not nullify the analogy as the resultant force can be split into orthogonal components and each dealt with in the same way.
A simplified explanation for the integration of the pressure over the contact area may be stated as follows:
Consider a cube immersed in a fluid with the upper surface horizontal.
The sides are identical in area, and have the same depth distribution, therefore they also have the same pressure distribution, and consequently the same total force resulting from hydrostatic pressure, exerted perpendicular to the plane of the surface of each side.
There are two pairs of opposing sides, therefore the resultant horizontal forces balance in both orthogonal directions, and the resultant force is zero.
The upward force on the cube is the pressure on the bottom surface integrated over its area. The surface is at constant depth, so the pressure is constant. Therefore, the integral of the pressure over the area of the horizontal bottom surface of the cube is the hydrostatic pressure at that depth multiplied by the area of the bottom surface.
Similarly, the downward force on the cube is the pressure on the top surface integrated over its area. The surface is at constant depth, so the pressure is constant. Therefore, the integral of the pressure over the area of the horizontal top surface of the cube is the hydrostatic pressure at that depth multiplied by the area of the top surface.
As this is a cube, the top and bottom surfaces are identical in shape and area, and the pressure difference between the top and bottom of the cube is directly proportional to the depth difference, and the resultant force difference is exactly equal to the weight of the fluid that would occupy the volume of the cube in its absence.
This means that the resultant upward force on the cube is equal to the weight of the fluid that would fit into the volume of the cube, and the downward force on the cube is its weight, in the absence of external forces.
This analogy is valid for variations in the size of the cube.
If two cubes are placed alongside each other with a face of each in contact, the pressures and resultant forces on the sides or parts thereof in contact are balanced and may be disregarded, as the contact surfaces are equal in shape, size and pressure distribution, therefore the buoyancy of two cubes in contact is the sum of the buoyancies of each cube. This analogy can be extended to an arbitrary number of cubes.
An object of any shape can be approximated as a group of cubes in contact with each other, and as the size of the cubes is decreased, the precision of the approximation increases. The limiting case for infinitely small cubes is the exact equivalence.
Angled surfaces do not nullify the analogy as the resultant force can be split into orthogonal components and each dealt with in the same way.
buoyant force
Buoyancy (), or upthrust, is the force exerted by a fluid opposing the weight of a partially or fully immersed object (which may be also be a parcel of fluid). In a column of fluid, pressure increases with depth as a result of the weight of t ...
that is exerted on a body immersed in a fluid
In physics, a fluid is a liquid, gas, or other material that may continuously motion, move and Deformation (physics), deform (''flow'') under an applied shear stress, or external force. They have zero shear modulus, or, in simpler terms, are M ...
, whether fully or partially, is equal to the weight
In science and engineering, the weight of an object is a quantity associated with the gravitational force exerted on the object by other objects in its environment, although there is some variation and debate as to the exact definition.
Some sta ...
of the fluid that the body displaces. Archimedes' principle is a law of physics
Scientific laws or laws of science are statements, based on repeated experiments or observations, that describe or predict a range of natural phenomena. The term ''law'' has diverse usage in many cases (approximate, accurate, broad, or narrow) ...
fundamental to fluid mechanics
Fluid mechanics is the branch of physics concerned with the mechanics of fluids (liquids, gases, and plasma (physics), plasmas) and the forces on them.
Originally applied to water (hydromechanics), it found applications in a wide range of discipl ...
. It was formulated by Archimedes
Archimedes of Syracuse ( ; ) was an Ancient Greece, Ancient Greek Greek mathematics, mathematician, physicist, engineer, astronomer, and Invention, inventor from the ancient city of Syracuse, Sicily, Syracuse in History of Greek and Hellenis ...
of Syracuse
Syracuse most commonly refers to:
* Syracuse, Sicily, Italy; in the province of Syracuse
* Syracuse, New York, USA; in the Syracuse metropolitan area
Syracuse may also refer to:
Places
* Syracuse railway station (disambiguation)
Italy
* Provi ...
.
Explanation
In ''On Floating Bodies
''On Floating Bodies'' () is a work, originally in two books, by Archimedes, one of the most important mathematicians, physicists, and engineers of antiquity. Thought to have been written towards the end of Archimedes' life, ''On Floating Bodies ...
'', Archimedes suggested that (c. 246 BC):
Archimedes' principle allows the buoyancy of any floating object partially or fully immersed in a fluid to be calculated. The downward force on the object is simply its weight. The upward, or buoyant, force on the object is that stated by Archimedes' principle above. Thus, the net force on the object is the difference between the magnitudes of the buoyant force and its weight. If this net force is positive, the object rises; if negative, the object sinks; and if zero, the object is neutrally buoyant—that is, it remains in place without either rising or sinking. In simple words, Archimedes' principle states that, when a body is partially or completely immersed in a fluid, it experiences an apparent loss in weight that is equal to the weight of the fluid displaced by the immersed part of the body(s).
Formula
Consider a cuboid immersed in a fluid, its top and bottom faces orthogonal to the direction of gravity (assumed constant across the cube's stretch). The fluid will exert anormal force
In mechanics, the normal force F_n is the component of a contact force that is perpendicular to the surface that an object contacts. In this instance '' normal'' is used in the geometric sense and means perpendicular, as opposed to the meanin ...
on each face, but only the normal forces on top and bottom will contribute to buoyancy. The pressure
Pressure (symbol: ''p'' or ''P'') is the force applied perpendicular to the surface of an object per unit area over which that force is distributed. Gauge pressure (also spelled ''gage'' pressure)The preferred spelling varies by country and eve ...
difference between the bottom and the top face is directly proportional to the height (difference in depth of submersion). Multiplying the pressure difference by the area of a face gives a net force on the cuboid—the buoyancy—equaling in magnitude the weight of the fluid displaced by the cuboid. By summing up sufficiently many arbitrarily small cuboids this reasoning may be extended to irregular shapes, and so, whatever the shape of the submerged body, the buoyant force is equal to the weight of the displaced fluid.
:
The weight
In science and engineering, the weight of an object is a quantity associated with the gravitational force exerted on the object by other objects in its environment, although there is some variation and debate as to the exact definition.
Some sta ...
of the displaced fluid is directly proportional to the volume of the displaced fluid (if the surrounding fluid is of uniform density). The apparent weight
In physics, apparent weight is a property of objects that corresponds to how heavy an object appears to be. The apparent weight of an object will differ from the ordinary weight of an object whenever the force of gravity acting on the object is n ...
of the object in the fluid is reduced, because of the force acting on it, which is called upthrust. In simple terms, the principle states that the buoyant force (Fb) on an object is equal to the weight of the fluid displaced by the object, or the density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...
( ρ) of the fluid multiplied by the submerged volume (V) times the gravity
In physics, gravity (), also known as gravitation or a gravitational interaction, is a fundamental interaction, a mutual attraction between all massive particles. On Earth, gravity takes a slightly different meaning: the observed force b ...
(g)
We can express this relation in the equation:
:
where denotes the buoyant force applied onto the submerged object, denotes the density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...
of the fluid, represents the volume of the displaced fluid and is the acceleration due to gravity
In physics, gravity (), also known as gravitation or a gravitational interaction, is a fundamental interaction, a mutual attraction between all massive particles. On Earth, gravity takes a slightly different meaning: the observed force b ...
.
Thus, among completely submerged objects with equal masses, objects with greater volume have greater buoyancy.
Suppose a rock's weight is measured as 10 newtons when suspended by a string in a vacuum
A vacuum (: vacuums or vacua) is space devoid of matter. The word is derived from the Latin adjective (neuter ) meaning "vacant" or "void". An approximation to such vacuum is a region with a gaseous pressure much less than atmospheric pressur ...
with gravity acting on it. Suppose that, when the rock is lowered into the water, it displaces water of weight 3 newtons. The force it then exerts on the string from which it hangs would be 10 newtons minus the 3 newtons of buoyant force: 10 − 3 = 7 newtons. Buoyancy reduces the apparent weight of an object. It is generally easier to lift an object through the water than it is to pull it out of the water.
For a fully submerged object, Archimedes' principle can be reformulated as follows:
:
then inserted into the quotient of weights, which has been expanded by the mutual volume
:
yields the formula below. The density of the immersed object relative to the density of the fluid can easily be calculated without measuring any volume is
:
(This formula is used for example in describing the measuring principle of a dasymeter
A dasymeter was meant initially as a device to demonstrate the buoyant effect of gases like air (as shown in the adjacent pictures). A dasymeter which allows weighing acts as a densimeter used to measure the density of gases.
Principle
The ...
and of hydrostatic weighing
Hydrostatic weighing, also referred to as underwater weighing, hydrostatic body composition analysis and hydrodensitometry, is a technique for measuring the density of a living person's body. It is a direct application of Archimedes' principl ...
.)
Example: If you drop wood into water, buoyancy will keep it afloat.
Example: A helium balloon in a moving car. When increasing speed or driving in a curve, the air moves in the opposite direction to the car's acceleration. However, due to buoyancy, the balloon is pushed "out of the way" by the air and will drift in the same direction as the car's acceleration.
When an object is immersed in a liquid, the liquid exerts an upward force, which is known as the buoyant force, that is proportional to the weight of the displaced liquid. Consequently, the net force acting on the object is equal to the difference between the weight of the object, or 'down' force, and the weight of the displaced fluid, or 'up' force. Equilibrium, or neutral buoyancy, is achieved when these two weights and thus forces are equal.
Forces and equilibrium
The equation to calculate the pressure inside a fluid in equilibrium is: : where f is the force density exerted by some outer field on the fluid, and ''σ'' is theCauchy stress tensor
In continuum mechanics, the Cauchy stress tensor (symbol \boldsymbol\sigma, named after Augustin-Louis Cauchy), also called true stress tensor or simply stress tensor, completely defines the state of stress at a point inside a material in the d ...
. In this case the stress tensor is proportional to the identity tensor:
:
Here ''δij'' is the Kronecker delta
In mathematics, the Kronecker delta (named after Leopold Kronecker) is a function of two variables, usually just non-negative integers. The function is 1 if the variables are equal, and 0 otherwise:
\delta_ = \begin
0 &\text i \neq j, \\
1 &\ ...
. Using this the above equation becomes:
:
Assuming the outer force field is conservative, that is it can be written as the negative gradient of some scalar valued function:
:
Then:
:
Therefore, the shape of the open surface of a fluid equals the equipotential plane of the applied outer conservative force field. Let the ''z''-axis point downward. In this case the field is gravity, so Φ = −''ρfgz'' where ''g'' is the gravitational acceleration, ''ρf'' is the mass density of the fluid. Taking the pressure as zero at the surface, where ''z'' is zero, the constant will be zero, so the pressure inside the fluid, when it is subject to gravity, is
:
So pressure increases with depth below the surface of a liquid, as ''z'' denotes the distance from the surface of the liquid into it. Any object with a non-zero vertical depth will have different pressures on its top and bottom, with the pressure on the bottom being greater. This difference in pressure causes the upward buoyancy force.
The buoyancy force exerted on a body can now be calculated easily, since the internal pressure of the fluid is known. The force exerted on the body can be calculated by integrating the stress tensor over the surface of the body which is in contact with the fluid:
:
The surface integral
In mathematics, particularly multivariable calculus, a surface integral is a generalization of multiple integrals to integration over surfaces. It can be thought of as the double integral analogue of the line integral. Given a surface, o ...
can be transformed into a volume integral
In mathematics (particularly multivariable calculus), a volume integral (∭) is an integral over a 3-dimensional domain; that is, it is a special case of multiple integrals. Volume integrals are especially important in physics for many applica ...
with the help of the Gauss theorem
In vector calculus, the divergence theorem, also known as Gauss's theorem or Ostrogradsky's theorem, reprinted in is a theorem relating the ''flux'' of a vector field through a closed surface to the ''divergence'' of the field in the volume en ...
:
:
where ''V'' is the measure of the volume in contact with the fluid, that is the volume of the submerged part of the body, since the fluid doesn't exert force on the part of the body which is outside of it.
The magnitude of buoyancy force may be appreciated a bit more from the following argument. Consider any object of arbitrary shape and volume ''V'' surrounded by a liquid. The force
In physics, a force is an influence that can cause an Physical object, object to change its velocity unless counterbalanced by other forces. In mechanics, force makes ideas like 'pushing' or 'pulling' mathematically precise. Because the Magnitu ...
the liquid exerts on an object within the liquid is equal to the weight of the liquid with a volume equal to that of the object. This force is applied in a direction opposite to gravitational force, that is of magnitude:
:
where ''ρf'' is the density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...
of the fluid, ''Vdisp'' is the volume of the displaced body of liquid, and ''g'' is the gravitational acceleration
In physics, gravitational acceleration is the acceleration of an object in free fall within a vacuum (and thus without experiencing drag (physics), drag). This is the steady gain in speed caused exclusively by gravitational attraction. All bodi ...
at the location in question.
If this volume of liquid is replaced by a solid body of exactly the same shape, the force the liquid exerts on it must be exactly the same as above. In other words, the "buoyancy force" on a submerged body is directed in the opposite direction to gravity and is equal in magnitude to
:
The net force
In mechanics, the net force is the sum of all the forces acting on an object. For example, if two forces are acting upon an object in opposite directions, and one force is greater than the other, the forces can be replaced with a single force tha ...
on the object must be zero if it is to be a situation of fluid statics such that Archimedes principle is applicable, and is thus the sum of the buoyancy force and the object's weight
:
If the buoyancy of an (unrestrained and unpowered) object exceeds its weight, it tends to rise. An object whose weight exceeds its buoyancy tends to sink. Calculation of the upwards force on a submerged object during its accelerating
In mechanics, acceleration is the rate of change of the velocity of an object with respect to time. Acceleration is one of several components of kinematics, the study of motion. Accelerations are vector quantities (in that they have magnit ...
period cannot be done by the Archimedes principle alone; it is necessary to consider dynamics of an object involving buoyancy. Once it fully sinks to the floor of the fluid or rises to the surface and settles, Archimedes principle can be applied alone. For a floating object, only the submerged volume displaces water. For a sunken object, the entire volume displaces water, and there will be an additional force of reaction from the solid floor.
In order for Archimedes' principle to be used alone, the object in question must be in equilibrium (the sum of the forces on the object must be zero), therefore;
:
and therefore
:
showing that the depth to which a floating object will sink, and the volume of fluid it will displace, is independent of the gravitational field
In physics, a gravitational field or gravitational acceleration field is a vector field used to explain the influences that a body extends into the space around itself. A gravitational field is used to explain gravitational phenomena, such as ...
regardless of geographic location.
: (''Note: If the fluid in question is seawater
Seawater, or sea water, is water from a sea or ocean. On average, seawater in the world's oceans has a salinity of about 3.5% (35 g/L, 35 ppt, 600 mM). This means that every kilogram (roughly one liter by volume) of seawater has approximat ...
, it will not have the same density
Density (volumetric mass density or specific mass) is the ratio of a substance's mass to its volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' (or ''d'') can also be u ...
(''ρ'') at every location. For this reason, a ship may display a Plimsoll line
The load line, also known as Plimsoll line, indicates the legal limit to which a ship may be loaded for specific water types and temperatures in order to safely maintain buoyancy, particularly with regard to the hazard of Wind wave, waves. The l ...
.)''
It can be the case that forces other than just buoyancy and gravity come into play. This is the case if the object is restrained or if the object sinks to the solid floor. An object which tends to float requires a tension restraint force T in order to remain fully submerged. An object which tends to sink will eventually have a normal force
In mechanics, the normal force F_n is the component of a contact force that is perpendicular to the surface that an object contacts. In this instance '' normal'' is used in the geometric sense and means perpendicular, as opposed to the meanin ...
of constraint N exerted upon it by the solid floor. The constraint force can be tension in a spring scale measuring its weight in the fluid, and is how apparent weight is defined.
If the object would otherwise float, the tension to restrain it fully submerged is:
:
When a sinking object settles on the solid floor, it experiences a normal force
In mechanics, the normal force F_n is the component of a contact force that is perpendicular to the surface that an object contacts. In this instance '' normal'' is used in the geometric sense and means perpendicular, as opposed to the meanin ...
of:
:
Another possible formula for calculating buoyancy of an object is by finding the apparent weight of that particular object in the air (calculated in Newtons), and apparent weight of that object in the water (in Newtons). To find the force of buoyancy acting on the object when in air, using this particular information, this formula applies:
: Buoyancy force = weight of object in empty space − weight of object immersed in fluid
The final result would be measured in Newtons.
Air's density is very small compared to most solids and liquids. For this reason, the weight of an object in air is approximately the same as its true weight in a vacuum. The buoyancy of air is neglected for most objects during a measurement in air because the error is usually insignificant (typically less than 0.1% except for objects of very low average density such as a balloon or light foam).
Simplified model


 A simplified explanation for the integration of the pressure over the contact area may be stated as follows:
Consider a cube immersed in a fluid with the upper surface horizontal.
The sides are identical in area, and have the same depth distribution, therefore they also have the same pressure distribution, and consequently the same total force resulting from hydrostatic pressure, exerted perpendicular to the plane of the surface of each side.
There are two pairs of opposing sides, therefore the resultant horizontal forces balance in both orthogonal directions, and the resultant force is zero.
The upward force on the cube is the pressure on the bottom surface integrated over its area. The surface is at constant depth, so the pressure is constant. Therefore, the integral of the pressure over the area of the horizontal bottom surface of the cube is the hydrostatic pressure at that depth multiplied by the area of the bottom surface.
Similarly, the downward force on the cube is the pressure on the top surface integrated over its area. The surface is at constant depth, so the pressure is constant. Therefore, the integral of the pressure over the area of the horizontal top surface of the cube is the hydrostatic pressure at that depth multiplied by the area of the top surface.
As this is a cube, the top and bottom surfaces are identical in shape and area, and the pressure difference between the top and bottom of the cube is directly proportional to the depth difference, and the resultant force difference is exactly equal to the weight of the fluid that would occupy the volume of the cube in its absence.
This means that the resultant upward force on the cube is equal to the weight of the fluid that would fit into the volume of the cube, and the downward force on the cube is its weight, in the absence of external forces.
This analogy is valid for variations in the size of the cube.
If two cubes are placed alongside each other with a face of each in contact, the pressures and resultant forces on the sides or parts thereof in contact are balanced and may be disregarded, as the contact surfaces are equal in shape, size and pressure distribution, therefore the buoyancy of two cubes in contact is the sum of the buoyancies of each cube. This analogy can be extended to an arbitrary number of cubes.
An object of any shape can be approximated as a group of cubes in contact with each other, and as the size of the cubes is decreased, the precision of the approximation increases. The limiting case for infinitely small cubes is the exact equivalence.
Angled surfaces do not nullify the analogy as the resultant force can be split into orthogonal components and each dealt with in the same way.
A simplified explanation for the integration of the pressure over the contact area may be stated as follows:
Consider a cube immersed in a fluid with the upper surface horizontal.
The sides are identical in area, and have the same depth distribution, therefore they also have the same pressure distribution, and consequently the same total force resulting from hydrostatic pressure, exerted perpendicular to the plane of the surface of each side.
There are two pairs of opposing sides, therefore the resultant horizontal forces balance in both orthogonal directions, and the resultant force is zero.
The upward force on the cube is the pressure on the bottom surface integrated over its area. The surface is at constant depth, so the pressure is constant. Therefore, the integral of the pressure over the area of the horizontal bottom surface of the cube is the hydrostatic pressure at that depth multiplied by the area of the bottom surface.
Similarly, the downward force on the cube is the pressure on the top surface integrated over its area. The surface is at constant depth, so the pressure is constant. Therefore, the integral of the pressure over the area of the horizontal top surface of the cube is the hydrostatic pressure at that depth multiplied by the area of the top surface.
As this is a cube, the top and bottom surfaces are identical in shape and area, and the pressure difference between the top and bottom of the cube is directly proportional to the depth difference, and the resultant force difference is exactly equal to the weight of the fluid that would occupy the volume of the cube in its absence.
This means that the resultant upward force on the cube is equal to the weight of the fluid that would fit into the volume of the cube, and the downward force on the cube is its weight, in the absence of external forces.
This analogy is valid for variations in the size of the cube.
If two cubes are placed alongside each other with a face of each in contact, the pressures and resultant forces on the sides or parts thereof in contact are balanced and may be disregarded, as the contact surfaces are equal in shape, size and pressure distribution, therefore the buoyancy of two cubes in contact is the sum of the buoyancies of each cube. This analogy can be extended to an arbitrary number of cubes.
An object of any shape can be approximated as a group of cubes in contact with each other, and as the size of the cubes is decreased, the precision of the approximation increases. The limiting case for infinitely small cubes is the exact equivalence.
Angled surfaces do not nullify the analogy as the resultant force can be split into orthogonal components and each dealt with in the same way.
Refinements
Archimedes' principle does not consider thesurface tension
Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension (physics), tension is what allows objects with a higher density than water such as razor blades and insects (e.g. Ge ...
(capillarity) acting on the body. Moreover, Archimedes' principle has been found to break down in complex fluid
Complex fluids are mixtures that have a coexistence between two Phase (matter) , phases: solid–liquid (Suspension (chemistry) , suspensions or solutions of macromolecules such as polymers), solid–gas (Granular material, granular), liquid–gas ...
s.
There is an exception to Archimedes' principle known as the bottom (or side) case. This occurs when a side of the object is touching the bottom (or side) of the vessel it is submerged in, and no liquid seeps in along that side. In this case, the net force has been found to be different from Archimedes' principle, as, since no fluid seeps in on that side, the symmetry of pressure is broken.
Principle of flotation
Archimedes' principle shows the buoyant force and displacement of fluid. However, the concept of Archimedes' principle can be applied when considering why objects float. Proposition 5 of Archimedes' treatise ''On Floating Bodies
''On Floating Bodies'' () is a work, originally in two books, by Archimedes, one of the most important mathematicians, physicists, and engineers of antiquity. Thought to have been written towards the end of Archimedes' life, ''On Floating Bodies ...
'' states that
In other words, for an object floating on a liquid surface (like a boat) or floating submerged in a fluid (like a submarine
A submarine (often shortened to sub) is a watercraft capable of independent operation underwater. (It differs from a submersible, which has more limited underwater capability.) The term "submarine" is also sometimes used historically or infor ...
in water or dirigible
An airship, dirigible balloon or dirigible is a type of aerostat ( lighter-than-air) aircraft that can navigate through the air flying under its own power. Aerostats use buoyancy from a lifting gas that is less dense than the surrounding ...
in air) the weight of the displaced fluid equals the weight of the object. Thus, only in the special case of floating does the buoyant force acting on an object equal the objects weight. Consider a 1-ton block of solid iron. As iron is nearly eight times as dense as water, it displaces only 1/8 ton of water when submerged, which is not enough to keep it afloat. Suppose the same iron block is reshaped into a bowl. It still weighs 1 ton, but when it is put in water, it displaces a greater volume of water than when it was a block. The deeper the iron bowl is immersed, the more water it displaces, and the greater the buoyant force acting on it. When the buoyant force equals 1 ton, it will sink no farther.
When any boat displaces a weight of water equal to its own weight, it floats. This is often called the "principle of flotation": A floating object displaces a weight of fluid equal to its own weight. Every ship, submarine, and dirigible must be designed to displace a weight of fluid at least equal to its own weight. A 10,000-ton ship's hull must be built wide enough, long enough and deep enough to displace 10,000 tons of water and still have some hull above the water to prevent it from sinking. It needs extra hull to fight waves that would otherwise fill it and, by increasing its mass, cause it to submerge. The same is true for vessels in air: a dirigible that weighs 100 tons needs to displace 100 tons of air. If it displaces more, it rises; if it displaces less, it falls. If the dirigible displaces exactly its weight, it hovers at a constant altitude.
While they are related to it, the principle of flotation and the concept that a submerged object displaces a volume of fluid equal to its own volume are ''not'' Archimedes' principle. Archimedes' principle, as stated above, equates the ''buoyant force'' to the weight of the fluid displaced.
One common point of confusion regarding Archimedes' principle is the meaning of displaced volume. Common demonstrations involve measuring the rise in water level when an object floats on the surface in order to calculate the displaced water. This measurement approach fails with a buoyant submerged object because the rise in the water level is directly related to the volume of the object and not the mass (except if the effective density of the object equals exactly the fluid density).
Eureka
Archimedes reportedly exclaimed "Eureka" after he realized how to detect whether a crown is made of impure gold. While he did not use Archimedes' principle in the widespread tale and used displaced water only for measuring the volume of the crown, there is an alternative approach using the principle: Balance the crown and pure gold on a scale in the air and then put the scale into water. According to Archimedes' principle, if the density of the crown differs from the density of pure gold, the scale will get out of balance under water.See also
*Phragmen's voting rules
Phragmén's voting rules are rules for multiwinner voting. They allow voters to vote for individual candidates rather than parties, but still guarantee proportional representation. They were published by Lars Edvard Phragmén in French and Swedi ...
– a ballot load balancing method analogous to the idea of Archimedes' principle.
* Ship stability
Ship stability is an area of naval architecture and ship design that deals with how a ship behaves at sea, both in still water and in waves, whether intact or damaged. Stability calculations focus on center of mass#center of gravity, centers of ...
– Archimedes's theory of displacement of fluid is a core principle of ship stability.
* List of eponymous laws
This list of eponymous laws provides links to articles on laws, principles, adages, and other succinct observations or predictions named after a person. In some cases the person named has coined the law – such as Parkinson's law. In others, ...
References
External links
* {{Authority control Fluid dynamicsPrinciple
A principle may relate to a fundamental truth or proposition that serves as the foundation for a system of beliefs or behavior or a chain of reasoning. They provide a guide for behavior or evaluation. A principle can make values explicit, so t ...
Force
Buoyancy
Scientific laws