Anharmonic Oscillator on:
[Wikipedia]
[Google]
[Amazon]
 In
In
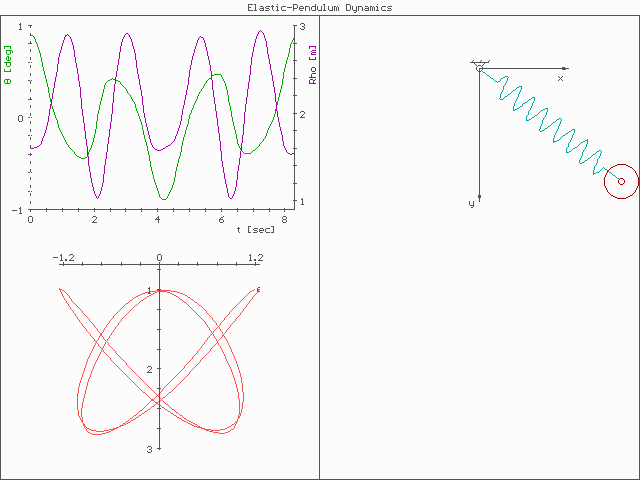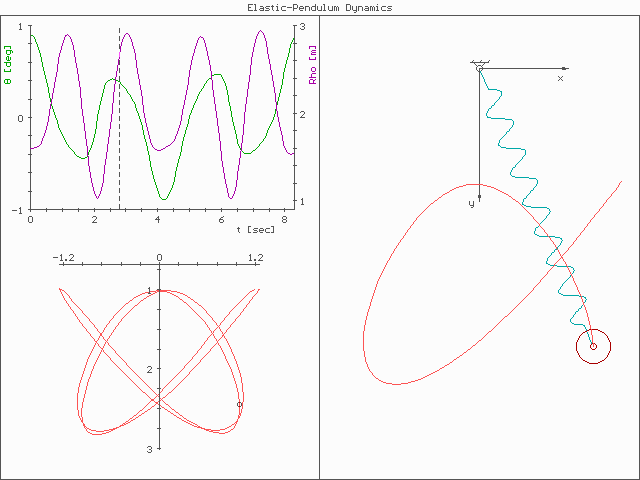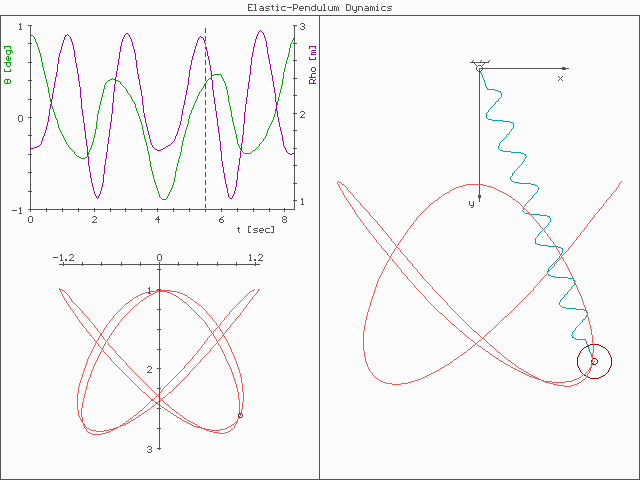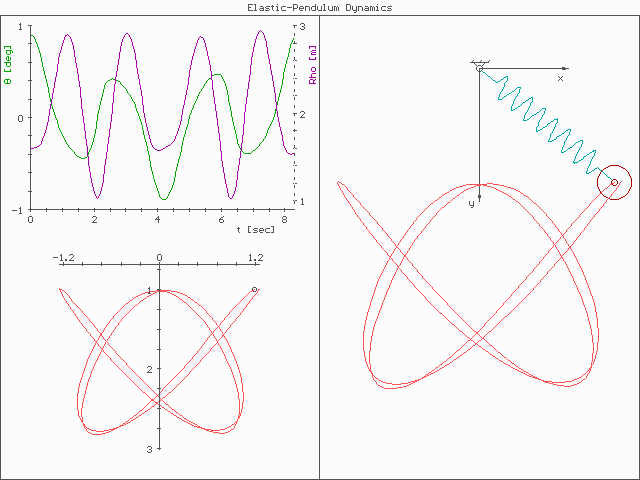 An oscillator is a physical system characterized by periodic motion, such as a pendulum, tuning fork, or vibrating
An oscillator is a physical system characterized by periodic motion, such as a pendulum, tuning fork, or vibrating
 In
In classical mechanics
Classical mechanics is a Theoretical physics, physical theory describing the motion of objects such as projectiles, parts of Machine (mechanical), machinery, spacecraft, planets, stars, and galaxies. The development of classical mechanics inv ...
, anharmonicity is the deviation of a system
A system is a group of interacting or interrelated elements that act according to a set of rules to form a unified whole. A system, surrounded and influenced by its open system (systems theory), environment, is described by its boundaries, str ...
from being a harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force ''F'' proportional to the displacement ''x'':
\vec F = -k \vec x,
where ''k'' is a positive const ...
. An oscillator
Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value (often a point of equilibrium) or between two or more different states. Familiar examples of oscillation include a swinging pendulum ...
that is not oscillating in harmonic motion is known as an anharmonic oscillator where the system can be approximated to a harmonic oscillator and the anharmonicity can be calculated using perturbation theory
In mathematics and applied mathematics, perturbation theory comprises methods for finding an approximate solution to a problem, by starting from the exact solution of a related, simpler problem. A critical feature of the technique is a middle ...
. If the anharmonicity is large, then other numerical techniques have to be used. In reality all oscillating systems are anharmonic, but most approximate the harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force ''F'' proportional to the displacement ''x'':
\vec F = -k \vec x,
where ''k'' is a positive const ...
the smaller the amplitude
The amplitude of a periodic variable is a measure of its change in a single period (such as time or spatial period). The amplitude of a non-periodic signal is its magnitude compared with a reference value. There are various definitions of am ...
of the oscillation is.
As a result, oscillations with frequencies
Frequency is the number of occurrences of a repeating event per unit of time. Frequency is an important parameter used in science and engineering to specify the rate of oscillatory and vibratory phenomena, such as mechanical vibrations, audio ...
and etc., where is the fundamental frequency
The fundamental frequency, often referred to simply as the ''fundamental'' (abbreviated as 0 or 1 ), is defined as the lowest frequency of a Periodic signal, periodic waveform. In music, the fundamental is the musical pitch (music), pitch of a n ...
of the oscillator, appear. Furthermore, the frequency deviates from the frequency of the harmonic oscillations. See also intermodulation
Intermodulation (IM) or intermodulation distortion (IMD) is the amplitude modulation of Signal (electrical engineering), signals containing two or more different frequencies, caused by non-linear, nonlinearities or time variance in a system. ...
and combination tones. As a first approximation, the frequency shift is proportional to the square of the oscillation amplitude
The amplitude of a periodic variable is a measure of its change in a single period (such as time or spatial period). The amplitude of a non-periodic signal is its magnitude compared with a reference value. There are various definitions of am ...
:
:
In a system of oscillators with natural frequencies
The fundamental frequency, often referred to simply as the ''fundamental'' (abbreviated as 0 or 1 ), is defined as the lowest frequency of a periodic waveform. In music, the fundamental is the musical pitch of a note that is perceived as the l ...
, , ... anharmonicity results in additional oscillations with frequencies .
Anharmonicity also modifies the energy profile of the resonance curve, leading to interesting phenomena such as the foldover effect and superharmonic
An overtone is any resonant frequency above the fundamental frequency of a sound. (An overtone may or may not be a harmonic) In other words, overtones are all pitches higher than the lowest pitch within an individual sound; the fundamental i ...
resonance.
General principle
 An oscillator is a physical system characterized by periodic motion, such as a pendulum, tuning fork, or vibrating
An oscillator is a physical system characterized by periodic motion, such as a pendulum, tuning fork, or vibrating diatomic molecule
Diatomic molecules () are molecules composed of only two atoms, of the same or different chemical elements. If a diatomic molecule consists of two atoms of the same element, such as hydrogen () or oxygen (), then it is said to be homonuclear mol ...
. Mathematically speaking, the essential feature of an oscillator is that for some coordinate of the system, a force whose magnitude depends on will push away from extreme values and back toward some central value , causing to oscillate between extremes. For example, may represent the displacement of a pendulum from its resting position . As the absolute value of increases, so does the restoring force acting on the pendulums weight that pushes it back towards its resting position.
In harmonic oscillators, the restoring force is proportional in magnitude (and opposite in direction) to the displacement of from its natural position . The resulting differential equation implies that must oscillate sinusoidally over time, with a period of oscillation that is inherent to the system. may oscillate with any amplitude, but will always have the same period.
Anharmonic oscillators, however, are characterized by the nonlinear dependence of the restorative force on the displacement x. Consequently, the anharmonic oscillator's period of oscillation may depend on its amplitude of oscillation.
As a result of the nonlinearity of anharmonic oscillators, the vibration frequency can change, depending upon the system's displacement. These changes in the vibration frequency result in energy being coupled from the fundamental vibration frequency to other frequencies through a process known as parametric coupling.
Treating the nonlinear restorative force as a function of the displacement of x from its natural position, we may replace by its linear approximation at zero displacement. The approximating function ''F1'' is linear, so it will describe simple harmonic motion. Further, this function is accurate when is small. For this reason, anharmonic motion can be approximated as harmonic motion as long as the oscillations are small.
Examples in physics
There are many systems throughout the physical world that can be modeled as anharmonic oscillators in addition to the nonlinear mass-spring system. For example, an atom, which consists of a positively charged nucleus surrounded by a negatively charged electronic cloud, experiences a displacement between the center of mass of the nucleus and the electronic cloud when an electric field is present. The amount of that displacement, called the electric dipole moment, is related linearly to the applied field for small fields, but as the magnitude of the field is increased, the field-dipole moment relationship becomes nonlinear, just as in the mechanical system. Further examples of anharmonic oscillators include the large-angle pendulum; nonequilibrium semiconductors that possess a large hot carrier population, which exhibit nonlinear behaviors of various types related to the effective mass of the carriers; and ionospheric plasmas, which also exhibit nonlinear behavior based on the anharmonicity of the plasma, transversal oscillating strings. In fact, virtually all oscillators become anharmonic when their pump amplitude increases beyond some threshold, and as a result it is necessary to use nonlinear equations of motion to describe their behavior. Anharmonicity plays a role in lattice and molecular vibrations, in quantum oscillations, and inacoustics
Acoustics is a branch of physics that deals with the study of mechanical waves in gases, liquids, and solids including topics such as vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician ...
. The atoms in a molecule or a solid vibrate about their equilibrium positions. When these vibrations have small amplitudes they can be described by harmonic oscillators
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force ''F'' proportional to the displacement ''x'':
\vec F = -k \vec x,
where ''k'' is a positive constan ...
. However, when the vibrational amplitudes are large, for example at high temperatures, anharmonicity becomes important. An example of the effects of anharmonicity is the thermal expansion of solids, which is usually studied within the quasi-harmonic approximation The quasi-harmonic approximation is a phonon-based model of solid-state physics used to describe volume-dependent thermal effects, such as the thermal expansion. It is based on the assumption that the harmonic approximation holds for every value of ...
. Studying vibrating anharmonic systems using quantum mechanics is a computationally demanding task because anharmonicity not only makes the potential experienced by each oscillator more complicated, but also introduces coupling between the oscillators. It is possible to use first-principles methods such as density-functional theory
Density functional theory (DFT) is a computational quantum mechanics, quantum mechanical modelling method used in physics, chemistry and materials science to investigate the electronic structure (or nuclear structure) (principally the ground sta ...
to map the anharmonic potential experienced by the atoms in both molecules and solids. Accurate anharmonic vibrational energies can then be obtained by solving the anharmonic vibrational equations for the atoms within a mean-field theory
In physics and probability theory, Mean-field theory (MFT) or Self-consistent field theory studies the behavior of high-dimensional random (stochastic) models by studying a simpler model that approximates the original by averaging over Degrees of ...
. Finally, it is possible to use Møller–Plesset perturbation theory
Møller–Plesset perturbation theory (MP) is one of several quantum chemistry post-Hartree–Fock ab initio methods in the field of computational chemistry. It improves on the Hartree–Fock method by adding electron correlation effects by me ...
to go beyond the mean-field formalism.
Period of oscillations
Consider a mass moving in a potential well . The oscillation period may be derived where the extremes of the motion are given by and .See also
*Inharmonicity
In music, inharmonicity is the degree to which the frequency, frequencies of overtones (also known as Harmonic series (music)#Partial, partials or partial tones) depart from Integer, whole multiples of the fundamental frequency (harmonic seri ...
*Harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force ''F'' proportional to the displacement ''x'':
\vec F = -k \vec x,
where ''k'' is a positive const ...
*Musical acoustics
Musical acoustics or music acoustics is a multidisciplinary field that combines knowledge from physics, psychophysics, organology (classification of the instruments), physiology, music theory, ethnomusicology, signal processing and instrument buil ...
*Nonlinear resonance In physics, nonlinear resonance is the occurrence of resonance in a nonlinear system. In nonlinear resonance the system behaviour – resonance frequency, resonance frequencies and normal mode, modes – depends on the amplitude of the oscillations, ...
* Transmon
References
* *External links
* {{Citation, last=Elmer , first=Franz-Josef , url=http://monet.physik.unibas.ch/~elmer/pendulum/nonres.htm , title=Nonlinear Resonance , publisher=University of Basel
The University of Basel (Latin: ''Universitas Basiliensis''; German: ''Universität Basel'') is a public research university in Basel, Switzerland. Founded on 4 April 1460, it is Switzerland's oldest university and among the world's oldest univ ...
, date=July 20, 1998 , accessdate=October 28, 2010 , url-status=dead , archiveurl=https://web.archive.org/web/20110613171204/http://monet.physik.unibas.ch/~elmer/pendulum/nonres.htm , archivedate=June 13, 2011
Classical mechanics