Alpha Max Plus Beta Min Algorithm

The alpha max plus beta min algorithm is a high-speed approximation of the square root of the sum of two squares. The square root of the sum of two squares, also known as Pythagorean addition, is a useful function, because it finds the hypotenuse of a right triangle given the two side lengths, the norm of a 2-D vector, or the magnitude $, z, = \sqrt$ of a complex number given the real and imaginary parts.

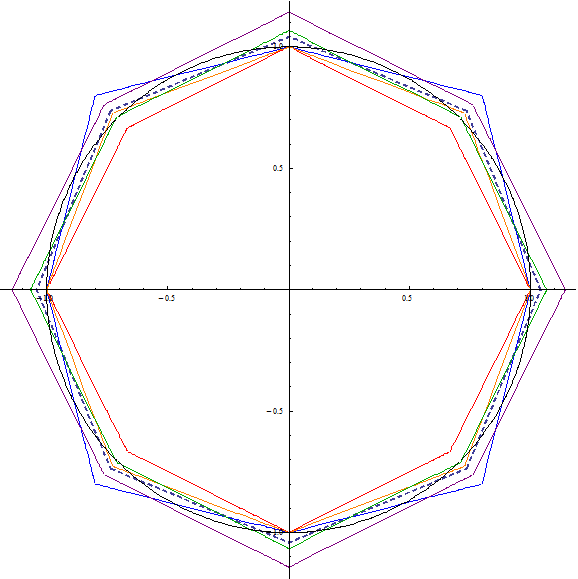
The algorithm avoids performing the square and square-root operations, instead using simple operations such as comparison, multiplication, and addition. Some choices of the α and β parameters of the algorithm allow the multiplication operation to be reduced to a simple shift of binary digits that is particularly well suited to implementation in high-speed digital circuitry.

The approximation is expressed as
$, z, = \alpha\,\mathbf + \beta\,\mathbf,$
where $\mathbf$ is the maximum absolute value of ''a'' and ''b'', and $\mathbf$ is the minimum absolute value of ''a'' and ''b''.

For the closest approximation, the optimum values for $\alpha$ and $\beta$ are $\alpha_0 = \frac = 0.960433870103...$ and $\beta_0 = \frac = 0.397824734759...$, giving a maximum error of 3.96%.

Improvements

When $\alpha < 1$, $, z,$ becomes smaller than $\mathbf$ (which is geometrically impossible) near the axes where $\mathbf$ is near 0.
This can be remedied by replacing the result with $\mathbf$ whenever that is greater, essentially splitting the line into two different segments.

: $, z, = \max(\mathbf, \alpha\,\mathbf + \beta\,\mathbf).$

Depending on the hardware, this improvement can be almost free.

Using this improvement changes which parameter values are optimal, because they no longer need a close match for the entire interval. A lower $\alpha$ and higher $\beta$ can therefore increase precision further.

''Increasing precision:'' When splitting the line in two like this one could improve precision even more by replacing the first segment by a better estimate than $\mathbf$, and adjust $\alpha$ and $\beta$ accordingly.

: $, z, = \max\big(, z_0, , , z_1, \big),$
: $, z_0, = \alpha_0\,\mathbf + \beta_0\,\mathbf,$
: $, z_1, = \alpha_1\,\mathbf + \beta_1\,\mathbf.$

Beware however, that a non-zero $\beta_0$ would require at least one extra addition and some bit-shifts (or a multiplication), probably nearly doubling the cost and, depending on the hardware, possibly defeat the purpose of using an approximation in the first place.

See also

*Hypot, a precise function or algorithm that is also safe against overflow and underflow.

References

* Lyons, Richard G. ''Understanding Digital Signal Processing, section 13.2.'' Prentice Hall, 2004 .
*Griffin, Grant
DSP Trick: Magnitude Estimator

External links

*{{cite web , title=Extension to three dimensions , date=May 14, 2015 , work=Stack Exchange , url=https://math.stackexchange.com/q/1282435

Approximation algorithms
Root-finding algorithms
Pythagorean theorem