All-Reduce on:
[Wikipedia]
[Google]
[Amazon]
Collective operations are building blocks for interaction patterns, that are often used in
 The reduce patternSanders, Mehlhorn, Dietzfelbinger, Dementiev 2019, pp. 402-403 is used to collect data or partial results from different processing units and to combine them into a global result by a chosen operator. Given processing units, message is on processing unit initially. All are aggregated by and the result is eventually stored on . The reduction operator must be associative at least. Some algorithms require a commutative operator with a neutral element. Operators like , , are common.
Implementation considerations are similar to broadcast (). For pipelining on
The reduce patternSanders, Mehlhorn, Dietzfelbinger, Dementiev 2019, pp. 402-403 is used to collect data or partial results from different processing units and to combine them into a global result by a chosen operator. Given processing units, message is on processing unit initially. All are aggregated by and the result is eventually stored on . The reduction operator must be associative at least. Some algorithms require a commutative operator with a neutral element. Operators like , , are common.
Implementation considerations are similar to broadcast (). For pipelining on
 The all-reduce patternSanders, Mehlhorn, Dietzfelbinger, Dementiev 2019, pp. 403-404 (also called allreduce) is used if the result of a reduce operation () must be distributed to all processing units. Given processing units, message is on processing unit initially. All are aggregated by an operator and the result is eventually stored on all . Analog to the reduce operation, the operator must be at least associative.
All-reduce can be interpreted as a reduce operation with a subsequent broadcast (). For long messages a corresponding implementation is suitable, whereas for short messages, the latency can be reduced by using a
The all-reduce patternSanders, Mehlhorn, Dietzfelbinger, Dementiev 2019, pp. 403-404 (also called allreduce) is used if the result of a reduce operation () must be distributed to all processing units. Given processing units, message is on processing unit initially. All are aggregated by an operator and the result is eventually stored on all . Analog to the reduce operation, the operator must be at least associative.
All-reduce can be interpreted as a reduce operation with a subsequent broadcast (). For long messages a corresponding implementation is suitable, whereas for short messages, the latency can be reduced by using a
 The gather communication patternSanders, Mehlhorn, Dietzfelbinger, Dementiev 2019, pp. 412-413 is used to store data from all processing units on a single processing unit. Given processing units, message on processing unit . For a fixed processing unit , we want to store the message on . Gather can be thought of as a reduce operation () that uses the concatenation operator. This works due to the fact that concatenation is associative. By using the same binomial tree reduction algorithm we get a runtime of . We see that the asymptotic runtime is similar to the asymptotic runtime of reduce , but with the addition of a factor p to the term . This additional factor is due to the message size increasing in each step as messages get concatenated. Compare this to reduce where message size is a constant for operators like .
The gather communication patternSanders, Mehlhorn, Dietzfelbinger, Dementiev 2019, pp. 412-413 is used to store data from all processing units on a single processing unit. Given processing units, message on processing unit . For a fixed processing unit , we want to store the message on . Gather can be thought of as a reduce operation () that uses the concatenation operator. This works due to the fact that concatenation is associative. By using the same binomial tree reduction algorithm we get a runtime of . We see that the asymptotic runtime is similar to the asymptotic runtime of reduce , but with the addition of a factor p to the term . This additional factor is due to the message size increasing in each step as messages get concatenated. Compare this to reduce where message size is a constant for operators like .
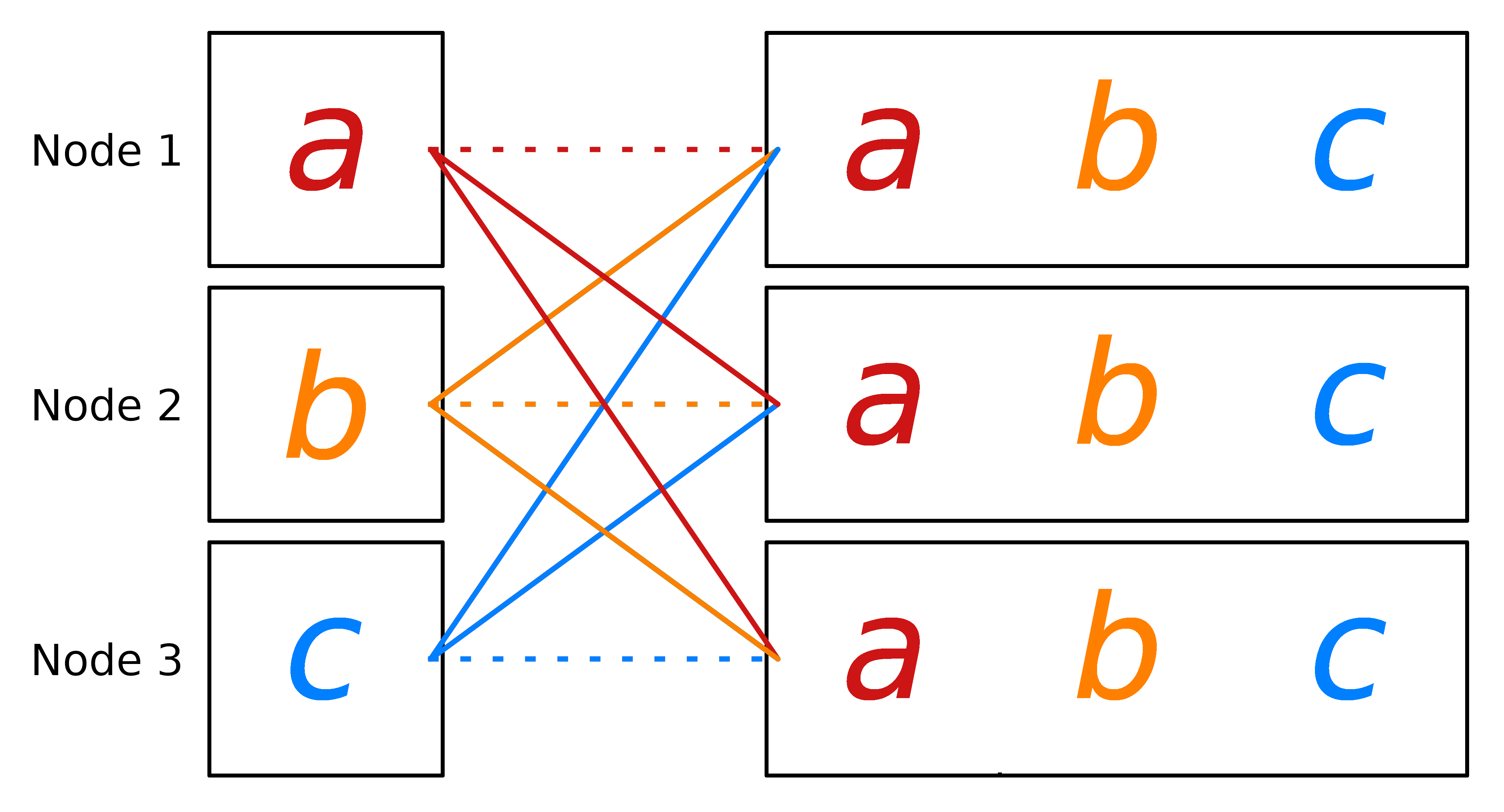 The all-gather communication pattern is used to collect data from all processing units and to store the collected data on all processing units. Given processing units , message initially stored on , we want to store the message on each .
It can be thought of in multiple ways. The first is as an all-reduce operation () with concatenation as the operator, in the same way that gather can be represented by reduce. The second is as a gather-operation followed by a broadcast of the new message of size . With this we see that all-gather in is possible.
The all-gather communication pattern is used to collect data from all processing units and to store the collected data on all processing units. Given processing units , message initially stored on , we want to store the message on each .
It can be thought of in multiple ways. The first is as an all-reduce operation () with concatenation as the operator, in the same way that gather can be represented by reduce. The second is as a gather-operation followed by a broadcast of the new message of size . With this we see that all-gather in is possible.
 The scatter communication patternSanders, Mehlhorn, Dietzfelbinger, Dementiev 2019, p. 413 is used to distribute data from one processing unit to all the processing units. It differs from broadcast, in that it does not send the same message to all processing units. Instead it splits the message and delivers one part of it to each processing unit.
Given processing units , a fixed processing unit that holds the message . We want to transport the message onto . The same implementation concerns as for gather () apply. This leads to an optimal runtime in .
The scatter communication patternSanders, Mehlhorn, Dietzfelbinger, Dementiev 2019, p. 413 is used to distribute data from one processing unit to all the processing units. It differs from broadcast, in that it does not send the same message to all processing units. Instead it splits the message and delivers one part of it to each processing unit.
Given processing units , a fixed processing unit that holds the message . We want to transport the message onto . The same implementation concerns as for gather () apply. This leads to an optimal runtime in .

SPMD
In computing, single program, multiple data (SPMD) is a term that has been used to refer to computational models for exploiting parallelism whereby multiple processors cooperate in the execution of a program in order to obtain results faster. ...
algorithms in the parallel programming
Parallel computing is a type of computing, computation in which many calculations or Process (computing), processes are carried out simultaneously. Large problems can often be divided into smaller ones, which can then be solved at the same time. ...
context. Hence, there is an interest in efficient realizations of these operations.
A realization of the collective operations is provided by the Message Passing Interface
The Message Passing Interface (MPI) is a portable message-passing standard designed to function on parallel computing architectures. The MPI standard defines the syntax and semantics of library routines that are useful to a wide range of use ...
(MPI).
Definitions
In all asymptotic runtime functions, we denote the latency (or startup time per message, independent of message size), the communication cost per word , the number of processing units and the input size per node . In cases where we have initial messages on more than one node we assume that all local messages are of the same size. To address individual processing units we use . If we do not have an equal distribution, i.e. node has a message of size , we get an upper bound for the runtime by setting . A distributed memory model is assumed. The concepts are similar for the shared memory model. However, shared memory systems can provide hardware support for some operations like broadcast () for example, which allows convenient concurrent read.Sanders, Mehlhorn, Dietzfelbinger, Dementiev 2019, p. 395 Thus, new algorithmic possibilities can become available.Broadcast
The broadcast patternSanders, Mehlhorn, Dietzfelbinger, Dementiev 2019, pp. 396-401 is used to distribute data from one processing unit to all processing units, which is often needed inSPMD
In computing, single program, multiple data (SPMD) is a term that has been used to refer to computational models for exploiting parallelism whereby multiple processors cooperate in the execution of a program in order to obtain results faster. ...
parallel programs to dispense input or global values. Broadcast can be interpreted as an inverse version of the reduce pattern (). Initially only root with stores message . During broadcast is sent to the remaining processing units, so that eventually is available to all processing units.
Since an implementation by means of a sequential for-loop with iterations becomes a bottleneck, divide-and-conquer approaches are common. One possibility is to utilize a binomial tree structure with the requirement that has to be a power of two. When a processing unit is responsible for sending to processing units , it sends to processing unit and delegates responsibility for the processing units to it, while its own responsibility is cut down to .
Binomial trees have a problem with long messages . The receiving unit of can only propagate the message to other units, after it received the whole message. In the meantime, the communication network is not utilized. Therefore pipelining on binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two children, referred to as the ''left child'' and the ''right child''. That is, it is a ''k''-ary tree with . A recursive definition using set theor ...
s is used, where is split into an array of packets of size . The packets are then broadcast one after another, so that data is distributed fast in the communication network.
Pipelined broadcast on balanced binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two children, referred to as the ''left child'' and the ''right child''. That is, it is a ''k''-ary tree with . A recursive definition using set theor ...
is possible in , whereas for the non-pipelined case it takes cost.
Reduce
 The reduce patternSanders, Mehlhorn, Dietzfelbinger, Dementiev 2019, pp. 402-403 is used to collect data or partial results from different processing units and to combine them into a global result by a chosen operator. Given processing units, message is on processing unit initially. All are aggregated by and the result is eventually stored on . The reduction operator must be associative at least. Some algorithms require a commutative operator with a neutral element. Operators like , , are common.
Implementation considerations are similar to broadcast (). For pipelining on
The reduce patternSanders, Mehlhorn, Dietzfelbinger, Dementiev 2019, pp. 402-403 is used to collect data or partial results from different processing units and to combine them into a global result by a chosen operator. Given processing units, message is on processing unit initially. All are aggregated by and the result is eventually stored on . The reduction operator must be associative at least. Some algorithms require a commutative operator with a neutral element. Operators like , , are common.
Implementation considerations are similar to broadcast (). For pipelining on binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two children, referred to as the ''left child'' and the ''right child''. That is, it is a ''k''-ary tree with . A recursive definition using set theor ...
s the message must be representable as a vector of smaller object for component-wise reduction.
Pipelined reduce on a balanced binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two children, referred to as the ''left child'' and the ''right child''. That is, it is a ''k''-ary tree with . A recursive definition using set theor ...
is possible in .
All-Reduce
 The all-reduce patternSanders, Mehlhorn, Dietzfelbinger, Dementiev 2019, pp. 403-404 (also called allreduce) is used if the result of a reduce operation () must be distributed to all processing units. Given processing units, message is on processing unit initially. All are aggregated by an operator and the result is eventually stored on all . Analog to the reduce operation, the operator must be at least associative.
All-reduce can be interpreted as a reduce operation with a subsequent broadcast (). For long messages a corresponding implementation is suitable, whereas for short messages, the latency can be reduced by using a
The all-reduce patternSanders, Mehlhorn, Dietzfelbinger, Dementiev 2019, pp. 403-404 (also called allreduce) is used if the result of a reduce operation () must be distributed to all processing units. Given processing units, message is on processing unit initially. All are aggregated by an operator and the result is eventually stored on all . Analog to the reduce operation, the operator must be at least associative.
All-reduce can be interpreted as a reduce operation with a subsequent broadcast (). For long messages a corresponding implementation is suitable, whereas for short messages, the latency can be reduced by using a hypercube
In geometry, a hypercube is an ''n''-dimensional analogue of a square ( ) and a cube ( ); the special case for is known as a ''tesseract''. It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel l ...
() topology, if is a power of two. All-reduce can also be implemented with a butterfly algorithm and achieve optimal latency and bandwidth.
All-reduce is possible in , since reduce and broadcast are possible in with pipelining on balanced binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two children, referred to as the ''left child'' and the ''right child''. That is, it is a ''k''-ary tree with . A recursive definition using set theor ...
s. All-reduce implemented with a butterfly algorithm achieves the same asymptotic runtime.
Prefix-Sum/Scan
The prefix-sum or scan operationSanders, Mehlhorn, Dietzfelbinger, Dementiev 2019, pp. 404-406 is used to collect data or partial results from different processing units and to compute intermediate results by an operator, which are stored on those processing units. It can be seen as a generalization of the reduce operation (). Given processing units, message is on processing unit . The operator must be at least associative, whereas some algorithms require also a commutative operator and a neutral element. Common operators are , and . Eventually processing unit stores the prefix sum . In the case of the so-called exclusive prefix sum, processing unit stores the prefix sum . Some algorithms require to store the overall sum at each processing unit in addition to the prefix sums. For short messages, this can be achieved with a hypercube topology if is a power of two. For long messages, thehypercube
In geometry, a hypercube is an ''n''-dimensional analogue of a square ( ) and a cube ( ); the special case for is known as a ''tesseract''. It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel l ...
(, ) topology is not suitable, since all processing units are active in every step and therefore pipelining can't be used. A binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two children, referred to as the ''left child'' and the ''right child''. That is, it is a ''k''-ary tree with . A recursive definition using set theor ...
topology is better suited for arbitrary and long messages ().
Prefix-sum on a binary tree can be implemented with an upward and downward phase. In the upward phase reduction is performed, while the downward phase is similar to broadcast, where the prefix sums are computed by sending different data to the left and right children. With this approach pipelining is possible, because the operations are equal to reduction () and broadcast ().
Pipelined prefix sum on a binary tree is possible in .
Barrier
The barrierSanders, Mehlhorn, Dietzfelbinger, Dementiev 2019, p. 408 as a collective operation is a generalization of the concept of a barrier, that can be used in distributed computing. When a processing unit calls barrier, it waits until all other processing units have called barrier as well. Barrier is thus used to achieve global synchronization in distributed computing. One way to implement barrier is to call all-reduce () with an empty/ dummy operand. We know the runtime of All-reduce is . Using a dummy operand reduces size to a constant factor and leads to a runtime of .Gather
 The gather communication patternSanders, Mehlhorn, Dietzfelbinger, Dementiev 2019, pp. 412-413 is used to store data from all processing units on a single processing unit. Given processing units, message on processing unit . For a fixed processing unit , we want to store the message on . Gather can be thought of as a reduce operation () that uses the concatenation operator. This works due to the fact that concatenation is associative. By using the same binomial tree reduction algorithm we get a runtime of . We see that the asymptotic runtime is similar to the asymptotic runtime of reduce , but with the addition of a factor p to the term . This additional factor is due to the message size increasing in each step as messages get concatenated. Compare this to reduce where message size is a constant for operators like .
The gather communication patternSanders, Mehlhorn, Dietzfelbinger, Dementiev 2019, pp. 412-413 is used to store data from all processing units on a single processing unit. Given processing units, message on processing unit . For a fixed processing unit , we want to store the message on . Gather can be thought of as a reduce operation () that uses the concatenation operator. This works due to the fact that concatenation is associative. By using the same binomial tree reduction algorithm we get a runtime of . We see that the asymptotic runtime is similar to the asymptotic runtime of reduce , but with the addition of a factor p to the term . This additional factor is due to the message size increasing in each step as messages get concatenated. Compare this to reduce where message size is a constant for operators like .
All-Gather
 The all-gather communication pattern is used to collect data from all processing units and to store the collected data on all processing units. Given processing units , message initially stored on , we want to store the message on each .
It can be thought of in multiple ways. The first is as an all-reduce operation () with concatenation as the operator, in the same way that gather can be represented by reduce. The second is as a gather-operation followed by a broadcast of the new message of size . With this we see that all-gather in is possible.
The all-gather communication pattern is used to collect data from all processing units and to store the collected data on all processing units. Given processing units , message initially stored on , we want to store the message on each .
It can be thought of in multiple ways. The first is as an all-reduce operation () with concatenation as the operator, in the same way that gather can be represented by reduce. The second is as a gather-operation followed by a broadcast of the new message of size . With this we see that all-gather in is possible.
Scatter
 The scatter communication patternSanders, Mehlhorn, Dietzfelbinger, Dementiev 2019, p. 413 is used to distribute data from one processing unit to all the processing units. It differs from broadcast, in that it does not send the same message to all processing units. Instead it splits the message and delivers one part of it to each processing unit.
Given processing units , a fixed processing unit that holds the message . We want to transport the message onto . The same implementation concerns as for gather () apply. This leads to an optimal runtime in .
The scatter communication patternSanders, Mehlhorn, Dietzfelbinger, Dementiev 2019, p. 413 is used to distribute data from one processing unit to all the processing units. It differs from broadcast, in that it does not send the same message to all processing units. Instead it splits the message and delivers one part of it to each processing unit.
Given processing units , a fixed processing unit that holds the message . We want to transport the message onto . The same implementation concerns as for gather () apply. This leads to an optimal runtime in .
All-to-all
All-to-allSanders, Mehlhorn, Dietzfelbinger, Dementiev 2019, pp. 413-418 is the most general communication pattern. For , message is the message that is initially stored on node and has to be delivered to node . We can express all communication primitives that do not use operators through all-to-all. For example, broadcast of message from node is emulated by setting for and setting empty for . Assuming we have a fully connected network, the best possible runtime for all-to-all is in . This is achieved through rounds of direct message exchange. For power of 2, in communication round , node exchanges messages with node . If the message size is small and latency dominates the communication, a hypercube algorithm can be used to distribute the messages in time .
Runtime Overview
This tableSanders, Mehlhorn, Dietzfelbinger, Dementiev 2019, p. 394 gives an overview over the best known asymptotic runtimes, assuming we have free choice of network topology. Example topologies we want for optimal runtime arebinary tree
In computer science, a binary tree is a tree data structure in which each node has at most two children, referred to as the ''left child'' and the ''right child''. That is, it is a ''k''-ary tree with . A recursive definition using set theor ...
, binomial tree, hypercube
In geometry, a hypercube is an ''n''-dimensional analogue of a square ( ) and a cube ( ); the special case for is known as a ''tesseract''. It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel l ...
.
In practice, we have to adjust to the available physical topologies, e.g. dragonfly, fat tree
The fat tree network is a universal network for provably efficient communication. It was invented by Charles E. Leiserson of the MIT in 1985. k-ary n-trees, the type of fat-trees commonly used in most high-performance networks, were initially ...
, grid network
A grid network is a computer network consisting of a number of computer systems connected in a grid topology.
In a regular grid topology, each node in the network is connected with two neighbors along one or more dimensions. If the network is o ...
(references other topologies, too).
More information under Network topology
Network topology is the arrangement of the elements (Data link, links, Node (networking), nodes, etc.) of a communication network. Network topology can be used to define or describe the arrangement of various types of telecommunication networks, ...
.
For each operation, the optimal algorithm can depend on the input sizes . For example, broadcast for short messages is best implemented using a binomial tree whereas for long messages a pipelined communication on a balanced binary tree is optimal.
The complexities stated in the table depend on the latency and the communication cost per word in addition to the number of processing units and the input message size per node . The ''# senders'' and ''# receivers'' columns represent the number of senders and receivers that are involved in the operation respectively. The ''# messages'' column lists the number of input messages and the ''Computations?'' column indicates if any computations are done on the messages or if the messages are just delivered without processing. ''Complexity'' gives the asymptotic runtime complexity of an optimal implementation under free choice of topology.
Notes
References
{{cite book, last1=Sanders, first1=Peter, title=Sequential and Parallel Algorithms and Data Structures - The Basic Toolbox, last2=Mehlhorn, first2=Kurt, last3=Dietzfelbinger, first3=Martin, last4=Dementiev, first4=Roman, date=2019, publisher=Springer Nature Switzerland AG, isbn=978-3-030-25208-3, authorlink1=Peter Sanders (computer scientist), authorlink2=Kurt Mehlhorn Parallel computing Algorithms Distributed computing