Adventures Among The Toroids on:
[Wikipedia]
[Google]
[Amazon]
''Adventures Among the Toroids: A study of orientable polyhedra with regular faces'' is a book on
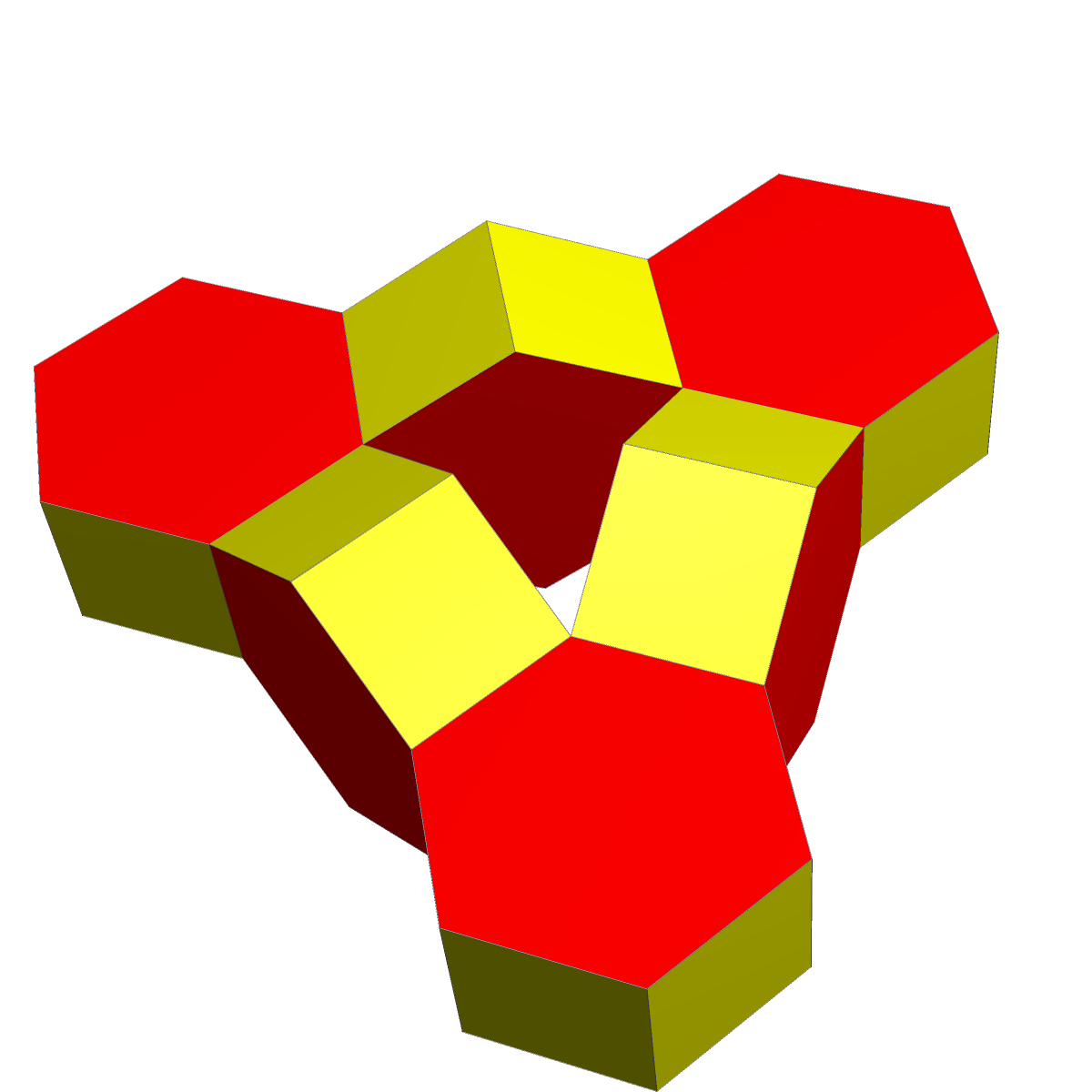 The
The  The second edition is rewritten in a different page format, letter sized in landscape mode compared to the tall and narrow by page size of the first edition, with two columns per page. It includes new material on knotted polyhedra and on rings of regular octahedra and regular dodecahedra; as the ring of dodecahedra forms the outline of a
The second edition is rewritten in a different page format, letter sized in landscape mode compared to the tall and narrow by page size of the first edition, with two columns per page. It includes new material on knotted polyhedra and on rings of regular octahedra and regular dodecahedra; as the ring of dodecahedra forms the outline of a
Virtual reality models of Stewart's polyhedra
Alex Doskey
Bonnie Stewarts Hohlkörper
(in German), Christoph Pöppe, on the German-language site of ''Scientific American'' Polyhedra Mathematics books 1970 non-fiction books 1980 non-fiction books Self-published books
toroidal polyhedra
In geometry, a toroidal polyhedron is a polyhedron which is also a toroid (a -holed torus), having a topology (Mathematics), topological Genus (mathematics), genus () of 1 or greater. Notable examples include the Császár polyhedron, Császár a ...
that have regular polygon
In Euclidean geometry, a regular polygon is a polygon that is Equiangular polygon, direct equiangular (all angles are equal in measure) and Equilateral polygon, equilateral (all sides have the same length). Regular polygons may be either ''convex ...
s as their faces. It was written, hand-lettered, and illustrated by mathematician Bonnie Stewart
Bonnie Madison Stewart (July 10, 1914 – April 15, 1994) was a professor of mathematics at Michigan State University from 1940 to 1980. He earned his Ph.D. from the University of Wisconsin–Madison in 1941, under the supervision of Cyrus Colton ...
, and self-published under the imprint "Number One Tall Search Book" in 1970. Stewart put out a second edition, again hand-lettered and self-published, in 1980. Although out of print, the Basic Library List Committee of the Mathematical Association of America
The Mathematical Association of America (MAA) is a professional society that focuses on mathematics accessible at the undergraduate level. Members include university
A university () is an educational institution, institution of tertiary edu ...
has recommended its inclusion in undergraduate mathematics libraries.
Topics
 The
The Platonic solid
In geometry, a Platonic solid is a Convex polytope, convex, regular polyhedron in three-dimensional space, three-dimensional Euclidean space. Being a regular polyhedron means that the face (geometry), faces are congruence (geometry), congruent (id ...
s, known to antiquity, have all faces regular polygons, all symmetric to each other (each face can be taken to each other face by a symmetry of the polyhedron). However, if less symmetry is required, a greater number of polyhedra can be formed while having all faces regular. The convex polyhedra
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal faces, straight edges and sharp corners or vertices. The term "polyhedron" may refer either to a solid figure or to its boundary surfa ...
with all faces regular were catalogued in 1966 by Norman Johnson (after earlier study e.g. by Martyn Cundy
Henry Martyn Cundy (23 December 1913 – 25 February 2005) was a mathematics teacher and professor in Britain and Malawi as well as a singer, musician and poet. He was one of the founders of the School Mathematics Project to reform O level and ...
and A. P. Rollett), and have come to be known as the Johnson solid
In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two Solid geometry, s ...
s. ''Adventures Among the Toroids'' extends the investigation of polyhedra with regular faces to non-convex polyhedra, and in particular to polyhedra of higher genus
Genus (; : genera ) is a taxonomic rank above species and below family (taxonomy), family as used in the biological classification of extant taxon, living and fossil organisms as well as Virus classification#ICTV classification, viruses. In bino ...
than the sphere. Many of these polyhedra can be formed by gluing together smaller polyhedral pieces, carving polyhedral tunnels through them, or piling them into elaborate towers. The toroidal polyhedra described in this book, formed from regular polygons with no self-intersections or flat angles, have come to be called Stewart toroid
In geometry, a toroidal polyhedron is a polyhedron which is also a toroid (a -holed torus), having a topological genus () of 1 or greater. Notable examples include the Császár and Szilassi polyhedra.
Variations in definition
Toroidal polyhed ...
s.
 The second edition is rewritten in a different page format, letter sized in landscape mode compared to the tall and narrow by page size of the first edition, with two columns per page. It includes new material on knotted polyhedra and on rings of regular octahedra and regular dodecahedra; as the ring of dodecahedra forms the outline of a
The second edition is rewritten in a different page format, letter sized in landscape mode compared to the tall and narrow by page size of the first edition, with two columns per page. It includes new material on knotted polyhedra and on rings of regular octahedra and regular dodecahedra; as the ring of dodecahedra forms the outline of a golden rhombus
In geometry, a golden rhombus is a rhombus whose diagonals are in the golden ratio:
: = \varphi = \approx 1.618~034
Equivalently, it is the Varignon parallelogram formed from the edge midpoints of a golden rectangle.
Rhombi with this shape f ...
, it can be extended to make skeletal pentagon-faced versions of the convex polyhedra formed from the golden rhombus, including the Bilinski dodecahedron
In geometry, the Bilinski dodecahedron is a Convex set, convex polyhedron with twelve Congruence (geometry), congruent golden rhombus faces. It has the same topology as the face-transitive rhombic dodecahedron, but a different geometry. It is a ...
, rhombic icosahedron
The rhombic icosahedron is a polyhedron shaped like an Oblate spheroid, oblate sphere. Its 20 faces are Congruence (geometry), congruent golden rhombi; 3, 4, or 5 faces meet at each vertex. It has 5 faces (green on top figure) meeting at each of ...
, and rhombic triacontahedron
The rhombic triacontahedron, sometimes simply called the triacontahedron as it is the most common thirty-faced polyhedron, is a convex polyhedron with 30 rhombus, rhombic face (geometry), faces. It has 60 edge (geometry), edges and 32 vertex ...
. The second edition also includes the Császár polyhedron
In geometry, the Császár polyhedron () is a nonconvex toroidal polyhedron with 14 triangular faces.
This polyhedron has no diagonals; every pair of vertices is connected by an edge. The seven vertices and 21 edges of the Császár polyhedron ...
and Szilassi polyhedron
In geometry, the Szilassi polyhedron is a nonconvex polyhedron, topologically a Toroidal polyhedron, torus, with seven hexagon, hexagonal faces. The tetrahedron and the Szilassi polyhedron are the only two known polyhedra in which each face share ...
, toroidal polyhedra with non-regular faces but with pairwise adjacent vertices and faces respectively, and constructions by Alaeglu and Giese of polyhedra with irregular but congruent faces and with the same numbers of edges at every vertex.
Audience and reception
The second edition describes its intended audience in an elaborate subtitle, a throwback to times when long subtitles were more common: "a study of Quasi-Convex, aplanar, tunneled orientable polyhedra of positive genus having regular faces with disjoint interiors, being an elaborate description and instructions for the construction of an enormous number or new and fascinating mathematical models of interest to students of euclidean geometry and topology, both secondary and collegiate, to designers, engineers and architects, to the scientific audience concerned with molecular and other structural problems, and to mathematicians, both professional and dilettante, with hundreds of exercises and search projects, many outlined for self-instruction". Reviewer H. S. M. Coxeter summarizes the book as "a remarkable combination of sound mathematics, art, instruction and humor", whileHenry Crapo
Henry Howland Crapo (pronounced ''Cray-poe''; May 24, 1804 – July 23, 1869) was a businessman and politician who was the 14th governor of Michigan from 1865 to 1869, during the end of the American Civil War and the beginning of Reconstruction. ...
calls it "highly recommended" to others interested in polyhedra and their juxtapositions.
Mathematician Joseph A. Troccolo calls a method of constructing physical models of polyhedra developed in the book, using cardboard and rubber bands, "of inestimable value in the classroom". One virtue of this technique is that it allows for the quick disassembly and reuse of its parts.
See also
*List of books about polyhedra
A list is a set of discrete items of information collected and set forth in some format for utility, entertainment, or other purposes. A list may be memorialized in any number of ways, including existing only in the mind of the list-maker, but ...
References
{{reflist, refs= {{citation, title=Review of ''Adventures Among the Toroids'' (1st ed.), first=H. S. M., last=Coxeter, authorlink=Harold Scott MacDonald Coxeter, journal=Mathematical Reviews
''Mathematical Reviews'' is a journal published by the American Mathematical Society (AMS) that contains brief synopses, and in some cases evaluations, of many articles in mathematics, statistics, and theoretical computer science.
The AMS also pu ...
, mr=0275266
{{citation, title=Review of ''Adventures Among the Toroids'' (2nd ed.), first=H. S. M., last=Coxeter, authorlink=Harold Scott MacDonald Coxeter, journal=Mathematical Reviews
''Mathematical Reviews'' is a journal published by the American Mathematical Society (AMS) that contains brief synopses, and in some cases evaluations, of many articles in mathematics, statistics, and theoretical computer science.
The AMS also pu ...
, mr=0588511, year=1982
{{citation, title=Review of ''Adventures Among the Toroids'' (2nd ed.), first=Henry, last=Crapo, authorlink=Henry Crapo (mathematician), journal=Structural Topology, volume=5, year=1980, url=http://www-iri.upc.es/people/ros/StructuralTopology/ST5/st5-09-a5-ocr.pdf, pages=45–48
{{citation, title=Adventures Among the Toroids (unreviewed listing), work=MAA Reviews, publisher=Mathematical Association of America
The Mathematical Association of America (MAA) is a professional society that focuses on mathematics accessible at the undergraduate level. Members include university
A university () is an educational institution, institution of tertiary edu ...
, url=https://old.maa.org/press/maa-reviews/adventures-among-the-toroids, accessdate=2020-08-01
{{citation, title=Review of ''Adventures Among the Toroids'' (1st ed.), journal=zbMATH
zbMATH Open, formerly Zentralblatt MATH, is a major reviewing service providing reviews and abstracts for articles in pure and applied mathematics, produced by the Berlin office of FIZ Karlsruhe – Leibniz Institute for Information Infrastru ...
, zbl=0214.47703, language=German
{{citation, title=Review of ''Adventures Among the Toroids'' (2nd ed.), journal=zbMATH
zbMATH Open, formerly Zentralblatt MATH, is a major reviewing service providing reviews and abstracts for articles in pure and applied mathematics, produced by the Berlin office of FIZ Karlsruhe – Leibniz Institute for Information Infrastru ...
, zbl=0443.52005
{{citation, url=https://www.software3d.com/PolyNav/PolyNavigator.php, last=Webb, first=Robert, title=Stella: Polyhedron Navigator, journal=Symmetry: Culture and Science, volume=11, issue=1–4, pages=231–268, year=2000
{{citation
, last = Troccolo , first = Joseph A.
, date = March 1976
, issue = 3
, journal = The Mathematics Teacher
, jstor = 27960432
, pages = 220–224
, title = The algebra and geometry of polyhedra
, volume = 69, doi = 10.5951/MT.69.3.0220
{{citation
, last = Prichett , first = Gordon D.
, date = January 1976
, issue = 1
, journal = The Mathematics Teacher
, jstor = 27960351
, pages = 5–10
, title = Three-dimensional discovery
, volume = 69, doi = 10.5951/MT.69.1.0005
External links
Virtual reality models of Stewart's polyhedra
Alex Doskey
Bonnie Stewarts Hohlkörper
(in German), Christoph Pöppe, on the German-language site of ''Scientific American'' Polyhedra Mathematics books 1970 non-fiction books 1980 non-fiction books Self-published books