Advection on:
[Wikipedia]
[Google]
[Amazon]
In the fields of
 Solutions to the advection equation can be approximated using
Solutions to the advection equation can be approximated using
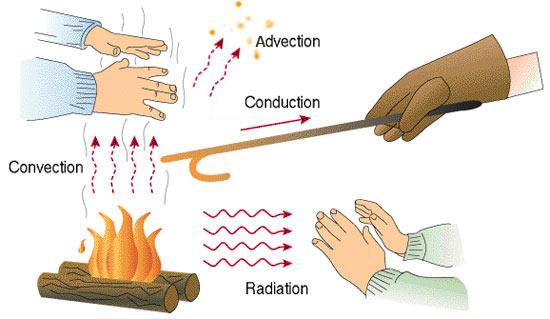 The term ''advection'' often serves as a synonym for ''
The term ''advection'' often serves as a synonym for ''
physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
, engineering
Engineering is the practice of using natural science, mathematics, and the engineering design process to Problem solving#Engineering, solve problems within technology, increase efficiency and productivity, and improve Systems engineering, s ...
, and earth science
Earth science or geoscience includes all fields of natural science related to the planet Earth. This is a branch of science dealing with the physical, chemical, and biological complex constitutions and synergistic linkages of Earth's four spheres ...
s, advection is the transport
Transport (in British English) or transportation (in American English) is the intentional Motion, movement of humans, animals, and cargo, goods from one location to another. Mode of transport, Modes of transport include aviation, air, land tr ...
of a substance or quantity by bulk motion of a fluid. The properties of that substance are carried with it. Generally the majority of the advected substance is also a fluid. The properties that are carried with the advected substance are conserved properties such as energy
Energy () is the physical quantity, quantitative physical property, property that is transferred to a physical body, body or to a physical system, recognizable in the performance of Work (thermodynamics), work and in the form of heat and l ...
. An example of advection is the transport of pollutants or silt
Silt is granular material of a size between sand and clay and composed mostly of broken grains of quartz. Silt may occur as a soil (often mixed with sand or clay) or as sediment mixed in suspension (chemistry), suspension with water. Silt usually ...
in a river
A river is a natural stream of fresh water that flows on land or inside Subterranean river, caves towards another body of water at a lower elevation, such as an ocean, lake, or another river. A river may run dry before reaching the end of ...
by bulk water flow downstream. Another commonly advected quantity is energy or enthalpy
Enthalpy () is the sum of a thermodynamic system's internal energy and the product of its pressure and volume. It is a state function in thermodynamics used in many measurements in chemical, biological, and physical systems at a constant extern ...
. Here the fluid may be any material that contains thermal energy, such as water
Water is an inorganic compound with the chemical formula . It is a transparent, tasteless, odorless, and Color of water, nearly colorless chemical substance. It is the main constituent of Earth's hydrosphere and the fluids of all known liv ...
or air. In general, any substance or conserved extensive quantity can be advected by a fluid
In physics, a fluid is a liquid, gas, or other material that may continuously motion, move and Deformation (physics), deform (''flow'') under an applied shear stress, or external force. They have zero shear modulus, or, in simpler terms, are M ...
that can hold or contain the quantity or substance.
During advection, a fluid transports some conserved quantity or material via bulk motion. The fluid's motion is described mathematically as a vector field, and the transported material is described by a scalar field
In mathematics and physics, a scalar field is a function associating a single number to each point in a region of space – possibly physical space. The scalar may either be a pure mathematical number ( dimensionless) or a scalar physical ...
showing its distribution over space. Advection requires currents in the fluid, and so cannot happen in rigid solids. It does not include transport of substances by molecular diffusion
Molecular diffusion is the motion of atoms, molecules, or other particles of a gas or liquid at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid, size and density (or their product, ...
.
Advection is sometimes confused with the more encompassing process of convection
Convection is single or Multiphase flow, multiphase fluid flow that occurs Spontaneous process, spontaneously through the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoy ...
, which is the combination of advective transport and diffusive transport.
In meteorology
Meteorology is the scientific study of the Earth's atmosphere and short-term atmospheric phenomena (i.e. weather), with a focus on weather forecasting. It has applications in the military, aviation, energy production, transport, agricultur ...
and physical oceanography, advection often refers to the transport of some property of the atmosphere or ocean
The ocean is the body of salt water that covers approximately 70.8% of Earth. The ocean is conventionally divided into large bodies of water, which are also referred to as ''oceans'' (the Pacific, Atlantic, Indian Ocean, Indian, Southern Ocean ...
, such as heat
In thermodynamics, heat is energy in transfer between a thermodynamic system and its surroundings by such mechanisms as thermal conduction, electromagnetic radiation, and friction, which are microscopic in nature, involving sub-atomic, ato ...
, humidity (see moisture
Moisture is the presence of a liquid, especially water, often in trace amounts. Moisture is defined as water in the adsorbed or absorbed phase. Small amounts of water may be found, for example, in the air (humidity), in foods, and in some comme ...
) or salinity
Salinity () is the saltiness or amount of salt (chemistry), salt dissolved in a body of water, called saline water (see also soil salinity). It is usually measured in g/L or g/kg (grams of salt per liter/kilogram of water; the latter is dimensio ...
.
Advection is important for the formation of orographic clouds and the precipitation of water from clouds, as part of the hydrological cycle.
Mathematical description
The advection equation is a first-orderhyperbolic partial differential equation
In mathematics, a hyperbolic partial differential equation of order n is a partial differential equation (PDE) that, roughly speaking, has a well-posed initial value problem for the first n - 1 derivatives. More precisely, the Cauchy problem can ...
that governs the motion of a conserved scalar field
In mathematics and physics, a scalar field is a function associating a single number to each point in a region of space – possibly physical space. The scalar may either be a pure mathematical number ( dimensionless) or a scalar physical ...
as it is advected by a known velocity vector field. It is derived using the scalar field's conservation law, together with Gauss's theorem, and taking the infinitesimal
In mathematics, an infinitesimal number is a non-zero quantity that is closer to 0 than any non-zero real number is. The word ''infinitesimal'' comes from a 17th-century Modern Latin coinage ''infinitesimus'', which originally referred to the " ...
limit.
One easily visualized example of advection is the transport of ink dumped into a river. As the river flows, ink will move downstream in a "pulse" via advection, as the water's movement itself transports the ink. If added to a lake without significant bulk water flow, the ink would simply disperse outwards from its source in a diffusive manner, which is not advection. Note that as it moves downstream, the "pulse" of ink will also spread via diffusion. The sum of these processes is called convection
Convection is single or Multiphase flow, multiphase fluid flow that occurs Spontaneous process, spontaneously through the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoy ...
.
The advection equation
The advection equation for a conserved quantity described by ascalar field
In mathematics and physics, a scalar field is a function associating a single number to each point in a region of space – possibly physical space. The scalar may either be a pure mathematical number ( dimensionless) or a scalar physical ...
is expressed by a continuity equation:
where vector field is the flow velocity and is the del operator.The subscripts denote the coordinates of the vector field; not to be confused with the notation for partial derivatives. If the flow is assumed to be incompressible then is solenoidal, that is, the divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the rate that the vector field alters the volume in an infinitesimal neighborhood of each point. (In 2D this "volume" refers to ...
is zero:and (by using a product rule associated with the divergence) the above equation reduces to
In particular, if the flow is steady, thenwhich shows that is constant (because for any vector ) along a streamline.
If a vector quantity (such as a magnetic field
A magnetic field (sometimes called B-field) is a physical field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular ...
) is being advected by the solenoidal velocity field , then the advection equation above becomes:
Here, is a vector field instead of the scalar field
In mathematics and physics, a scalar field is a function associating a single number to each point in a region of space – possibly physical space. The scalar may either be a pure mathematical number ( dimensionless) or a scalar physical ...
.
Solution
 Solutions to the advection equation can be approximated using
Solutions to the advection equation can be approximated using numerical methods
Numerical analysis is the study of algorithms that use numerical approximation (as opposed to symbolic manipulations) for the problems of mathematical analysis (as distinguished from discrete mathematics). It is the study of numerical methods t ...
, where interest typically centers on discontinuous "shock" solutions and necessary conditions for convergence (e.g. the CFL condition).
Numerical simulation can be aided by considering the skew-symmetric form of advection
where
Since skew symmetry implies only imaginary eigenvalues, this form reduces the "blow up" and "spectral blocking" often experienced in numerical solutions with sharp discontinuities.
Distinction between advection and convection
 The term ''advection'' often serves as a synonym for ''
The term ''advection'' often serves as a synonym for ''convection
Convection is single or Multiphase flow, multiphase fluid flow that occurs Spontaneous process, spontaneously through the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoy ...
'', and this correspondence of terms is used in the literature. More technically, convection applies to the movement of a fluid (often due to density gradients created by thermal gradients), whereas advection is the movement of some material by the velocity of the fluid. Thus, although it might seem confusing, it is technically correct to think of momentum being advected by the velocity field in the Navier-Stokes equations, although the resulting motion would be considered to be convection. Because of the specific use of the term convection to indicate transport in association with thermal gradients, it is probably safer to use the term advection if one is uncertain about which terminology best describes their particular system.
Meteorology
Inmeteorology
Meteorology is the scientific study of the Earth's atmosphere and short-term atmospheric phenomena (i.e. weather), with a focus on weather forecasting. It has applications in the military, aviation, energy production, transport, agricultur ...
and physical oceanography, advection often refers to the horizontal transport of some property of the atmosphere or ocean
The ocean is the body of salt water that covers approximately 70.8% of Earth. The ocean is conventionally divided into large bodies of water, which are also referred to as ''oceans'' (the Pacific, Atlantic, Indian Ocean, Indian, Southern Ocean ...
, such as heat
In thermodynamics, heat is energy in transfer between a thermodynamic system and its surroundings by such mechanisms as thermal conduction, electromagnetic radiation, and friction, which are microscopic in nature, involving sub-atomic, ato ...
, humidity or salinity, and convection generally refers to vertical transport (vertical advection). Advection is important for the formation of orographic clouds (terrain-forced convection) and the precipitation of water from clouds, as part of the hydrological cycle.
Other quantities
The advection equation also applies if the quantity being advected is represented by aprobability density function
In probability theory, a probability density function (PDF), density function, or density of an absolutely continuous random variable, is a Function (mathematics), function whose value at any given sample (or point) in the sample space (the s ...
at each point, although accounting for diffusion
Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical p ...
is more difficult.
See also
* Advection-diffusion equation *Atmosphere of Earth
The atmosphere of Earth is composed of a layer of gas mixture that surrounds the Earth's planetary surface (both lands and oceans), known collectively as air, with variable quantities of suspended aerosols and particulates (which create weather ...
* Conservation equation
* Courant–Friedrichs–Lewy condition
* Kinematic wave
* Overshoot (signal)
* Péclet number
* Radiation
In physics, radiation is the emission or transmission of energy in the form of waves or particles through space or a material medium. This includes:
* ''electromagnetic radiation'' consisting of photons, such as radio waves, microwaves, infr ...
Notes
References
* * {{Meteorological variables Vector calculus Atmospheric dynamics Conservation equations Equations of fluid dynamics Oceanography Convection Heat transfer Transport phenomena