Activity coefficient on:
[Wikipedia]
[Google]
[Amazon]
In

 The
The
 Activity coefficients of electrolyte solutions may be calculated theoretically, using the Debye–Hückel equation or extensions such as the Davies equation, Pitzer equations or TCPC model. Specific ion interaction theory (SIT) may also be used.
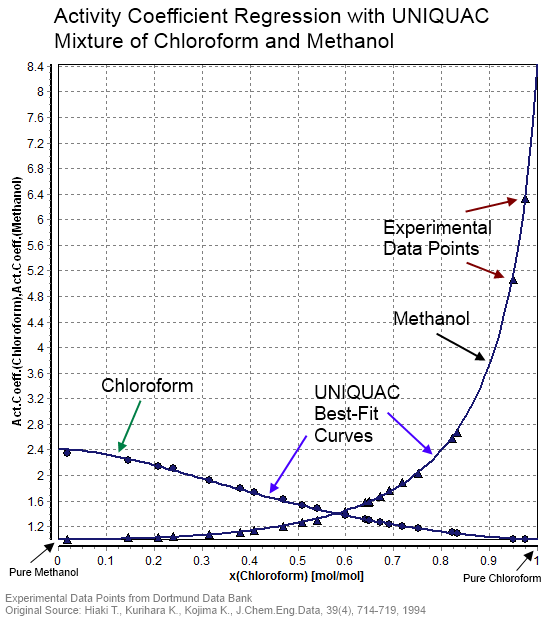
For non-electrolyte solutions correlative methods such as UNIQUAC, NRTL, MOSCED or UNIFAC may be employed, provided fitted component-specific or model parameters are available. COSMO-RS is a theoretical method which is less dependent on model parameters as required information is obtained from
Activity coefficients of electrolyte solutions may be calculated theoretically, using the Debye–Hückel equation or extensions such as the Davies equation, Pitzer equations or TCPC model. Specific ion interaction theory (SIT) may also be used.
For non-electrolyte solutions correlative methods such as UNIQUAC, NRTL, MOSCED or UNIFAC may be employed, provided fitted component-specific or model parameters are available. COSMO-RS is a theoretical method which is less dependent on model parameters as required information is obtained from
AIOMFAC online-model
An interactive group-contribution model for the calculation of activity coefficients in organic–inorganic mixtures.
''Electrochimica Acta''
Single-ion activity coefficients {{DEFAULTSORT:Activity Coefficient Thermodynamic models Equilibrium chemistry Dimensionless numbers of chemistry
thermodynamics
Thermodynamics is a branch of physics that deals with heat, Work (thermodynamics), work, and temperature, and their relation to energy, entropy, and the physical properties of matter and radiation. The behavior of these quantities is governed b ...
, an activity coefficient is a factor used to account for deviation of a mixture
In chemistry, a mixture is a material made up of two or more different chemical substances which can be separated by physical method. It is an impure substance made up of 2 or more elements or compounds mechanically mixed together in any proporti ...
of chemical substance
A chemical substance is a unique form of matter with constant chemical composition and characteristic properties. Chemical substances may take the form of a single element or chemical compounds. If two or more chemical substances can be com ...
s from ideal behaviour. In an ideal mixture, the microscopic interactions between each pair of chemical species are the same (or macroscopically equivalent, the enthalpy change of solution and volume variation in mixing is zero) and, as a result, properties of the mixtures can be expressed directly in terms of simple concentration
In chemistry, concentration is the abundance of a constituent divided by the total volume of a mixture. Several types of mathematical description can be distinguished: '' mass concentration'', '' molar concentration'', '' number concentration'', ...
s or partial pressure
In a mixture of gases, each constituent gas has a partial pressure which is the notional pressure of that constituent gas as if it alone occupied the entire volume of the original mixture at the same temperature. The total pressure of an ideal g ...
s of the substances present e.g. Raoult's law. Deviations from ideality are accommodated by modifying the concentration by an ''activity coefficient''. Analogously, expressions involving gases can be adjusted for non-ideality by scaling partial pressures by a fugacity coefficient.
The concept of activity coefficient is closely linked to that of activity in chemistry.
Thermodynamic definition
chemical potential
In thermodynamics, the chemical potential of a Chemical specie, species is the energy that can be absorbed or released due to a change of the particle number of the given species, e.g. in a chemical reaction or phase transition. The chemical potent ...
, , of a substance B in an ideal mixture of liquids or an ideal solution is given by
:,
where ''μ'' is the chemical potential of a pure substance , and is the mole fraction
In chemistry, the mole fraction or molar fraction, also called mole proportion or molar proportion, is a quantity defined as the ratio between the amount of a constituent substance, ''ni'' (expressed in unit of moles, symbol mol), and the to ...
of the substance in the mixture.
This is generalised to include non-ideal behavior by writing
:
when is the activity of the substance in the mixture,
:,
where is the activity coefficient, which may itself depend on . As approaches 1, the substance behaves as if it were ideal. For instance, if ≈ 1, then Raoult's law is accurate. For > 1 and < 1, substance B shows positive and negative deviation from Raoult's law, respectively. A positive deviation implies that substance B is more volatile.
In many cases, as goes to zero, the activity coefficient of substance B approaches a constant; this relationship is Henry's law for the solvent. These relationships are related to each other through the Gibbs–Duhem equation.
Note that in general activity coefficients are dimensionless.
In detail: Raoult's law states that the partial pressure of component B is related to its vapor pressure (saturation pressure) and its mole fraction in the liquid phase,
:
with the convention
In other words: Pure liquids represent the ideal case.
At infinite dilution, the activity coefficient approaches its limiting value, ∞. Comparison with Henry's law,
:
immediately gives
:
In other words: The compound shows nonideal behavior in the dilute case.
The above definition of the activity coefficient is impractical if the compound does not exist as a pure liquid. This is often the case for electrolytes or biochemical compounds. In such cases, a different definition is used that considers infinite dilution as the ideal state:
:
with
and
:
The symbol has been used here to distinguish between the two kinds of activity coefficients. Usually it is omitted, as it is clear from the context which kind is meant. But there are cases where both kinds of activity coefficients are needed and may even appear in the same equation, e.g., for solutions of salts in (water + alcohol) mixtures. This is sometimes a source of errors.
Modifying mole fractions or concentrations by activity coefficients gives the ''effective activities'' of the components, and hence allows expressions such as Raoult's law and equilibrium constant
The equilibrium constant of a chemical reaction is the value of its reaction quotient at chemical equilibrium, a state approached by a dynamic chemical system after sufficient time has elapsed at which its composition has no measurable tendency ...
s to be applied to both ideal and non-ideal mixtures.
Ionic solutions
Knowledge of activity coefficients is particularly important in the context ofelectrochemistry
Electrochemistry is the branch of physical chemistry concerned with the relationship between Electric potential, electrical potential difference and identifiable chemical change. These reactions involve Electron, electrons moving via an electronic ...
since the behaviour of electrolyte
An electrolyte is a substance that conducts electricity through the movement of ions, but not through the movement of electrons. This includes most soluble Salt (chemistry), salts, acids, and Base (chemistry), bases, dissolved in a polar solven ...
solutions is often far from ideal, even starting at low densities due to the effects of the ionic atmosphere. Additionally, they are particularly important in the context of soil chemistry
Soil chemistry is the study of the Chemistry, chemical characteristics of soil. Soil chemistry is affected by mineral composition, organic matter and Environment (biophysical), environmental factors. In the early 1870s a consulting chemist to the R ...
due to the low volumes of solvent and, consequently, the high concentration of electrolytes
An electrolyte is a substance that conducts electricity through the movement of ions, but not through the movement of electrons. This includes most soluble salts, acids, and bases, dissolved in a polar solvent like water. Upon dissolving, t ...
.
For solution of substances which ionize in solution the activity coefficients of the cation and anion cannot be experimentally determined independently of each other because solution properties depend on both ions. Single ion activity coefficients must be linked to the activity coefficient of the dissolved electrolyte as if undissociated. In this case a mean stoichiometric activity coefficient of the dissolved electrolyte, ''γ''±, is used. It is called stoichiometric because it expresses both the deviation from the ideality of the solution and the incomplete ionic dissociation of the ionic compound which occurs especially with the increase of its concentration.
For a 1:1 electrolyte, such as NaCl it is given by the following:
:
where and are the activity coefficients of the cation and anion respectively.
More generally, the mean activity coefficient of a compound of formula is given by
:
The prevailing view that single ion activity coefficients are unmeasurable independently, or perhaps even physically meaningless, has its roots in the work of Guggenheim in the late 1920s. In this view, the partitioning of the physical electrochemical potentials into an activity contribution and a Galvani potential contribution is arbitrary, thus nonidealities in ion activities can be remapped to nonidealities in Galvani potential and vice versa. Nevertheless, certain products of activities (such as ) reflect a charge-neutral stoichiometry that is anyway insensitive to this partitioning, so these products are physically meaningful even if the single-ion activities are not. However, chemists have never been able to give up the idea of single ion activities, and by implication single ion activity coefficients. For example, pH is defined as the negative logarithm of the hydrogen ion activity. If the prevailing view on the physical meaning and measurability of single ion activities is correct then defining pH as the negative logarithm of the hydrogen ion activity places the quantity squarely in the unmeasurable category. Recognizing this logical difficulty, International Union of Pure and Applied Chemistry
The International Union of Pure and Applied Chemistry (IUPAC ) is an international federation of National Adhering Organizations working for the advancement of the chemical sciences, especially by developing nomenclature and terminology. It is ...
(IUPAC) states that the activity-based definition of pH is a notional definition only. Despite the prevailing negative view on the measurability of single ion coefficients, the concept of single ion activities continues to be discussed in the literature.
Experimental determination of activity coefficients
Activity coefficients may be determined experimentally by making measurements on non-ideal mixtures. Use may be made of Raoult's law or Henry's law to provide a value for an ideal mixture against which the experimental value may be compared to obtain the activity coefficient. Other colligative properties, such asosmotic pressure
Osmotic pressure is the minimum pressure which needs to be applied to a Solution (chemistry), solution to prevent the inward flow of its pure solvent across a semipermeable membrane.
It is also defined as the measure of the tendency of a soluti ...
may also be used.
Radiochemical methods
Activity coefficients can be determined by radiochemical methods.At infinite dilution
Activity coefficients for binary mixtures are often reported at the infinite dilution of each component. Because activity coefficient models simplify at infinite dilution, such empirical values can be used to estimate interaction energies. Examples are given for water:Theoretical calculation of activity coefficients
 Activity coefficients of electrolyte solutions may be calculated theoretically, using the Debye–Hückel equation or extensions such as the Davies equation, Pitzer equations or TCPC model. Specific ion interaction theory (SIT) may also be used.
For non-electrolyte solutions correlative methods such as UNIQUAC, NRTL, MOSCED or UNIFAC may be employed, provided fitted component-specific or model parameters are available. COSMO-RS is a theoretical method which is less dependent on model parameters as required information is obtained from
Activity coefficients of electrolyte solutions may be calculated theoretically, using the Debye–Hückel equation or extensions such as the Davies equation, Pitzer equations or TCPC model. Specific ion interaction theory (SIT) may also be used.
For non-electrolyte solutions correlative methods such as UNIQUAC, NRTL, MOSCED or UNIFAC may be employed, provided fitted component-specific or model parameters are available. COSMO-RS is a theoretical method which is less dependent on model parameters as required information is obtained from quantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
calculations specific to each molecule (sigma profiles) combined with a statistical thermodynamics treatment of surface segments.
For uncharged species, the activity coefficient ''γ''0 mostly follows a salting-out model:
:
This simple model predicts activities of many species (dissolved undissociated gases such as CO2, H2S, NH3, undissociated acids and bases) to high ionic strengths (up to 5 mol/kg). The value of the constant ''b'' for CO2 is 0.11 at 10 °C and 0.20 at 330 °C.
For water
Water is an inorganic compound with the chemical formula . It is a transparent, tasteless, odorless, and Color of water, nearly colorless chemical substance. It is the main constituent of Earth's hydrosphere and the fluids of all known liv ...
as solvent, the activity ''a''w can be calculated using:
:
where ''ν'' is the number of ions produced from the dissociation of one molecule of the dissolved salt, ''b'' is the molality of the salt dissolved in water, ''φ'' is the osmotic coefficient of water, and the constant 55.51 represents the molality
In chemistry, molality is a measure of the amount of solute in a solution relative to a given mass of solvent. This contrasts with the definition of '' molarity'' which is based on a given volume of solution.
A commonly used unit for molality ...
of water. In the above equation, the activity of a solvent (here water) is represented as inversely proportional to the number of particles of salt versus that of the solvent.
Link to ionic diameter
The ionic activity coefficient is connected to the ionic diameter by the formula obtained from Debye–Hückel theory ofelectrolyte
An electrolyte is a substance that conducts electricity through the movement of ions, but not through the movement of electrons. This includes most soluble Salt (chemistry), salts, acids, and Base (chemistry), bases, dissolved in a polar solven ...
s:
:
where ''A'' and ''B'' are constants, ''zi'' is the valence number of the ion, and ''I'' is ionic strength.
Concentrated ionic solutions
Ionic activity coefficients can be calculated theoretically, for example by using the Debye–Hückel equation. The theoretical equation can be tested by combining the calculated single-ion activity coefficients to give mean values which can be compared to experimental values.Stokes–Robinson model
For concentrated ionic solutions the hydration of ions must be taken into consideration, as done by Stokes and Robinson in their hydration model from 1948. The activity coefficient of the electrolyte is split into electric and statistical components by E. Glueckauf who modifies the Robinson–Stokes model. The statistical part includes hydration index number , the number of ions from the dissociation and the ratio between the apparent molar volume of the electrolyte and the molar volume of water and molality . Concentrated solution statistical part of the activity coefficient is: : The Stokes–Robinson model has been analyzed and improved by other investigators. The problem with this widely accepted idea that electrolyte activity coefficients are driven at higher concentrations by changes in hydration is that water activities are completely dependent on the concentration of the ions themselves, as imposed by a thermodynamic relationship called the Gibbs-Duhem equation. This means that the activity coefficients and the corresponding water activities are linked together fundamentally, regardless of molecular-level hypotheses. Due to this high correlation, such hypotheses are not independent enough to be satisfactorily tested.Ion trios
The rise in activity coefficients found with most aqueous strong electrolyte systems can be explained by increasing electrostatic repulsions between ions of the same charge which are forced together as the available space between them decreases. In this way, the initial attractions between cations and anions at the low concentrations described by Debye and Hueckel are progressively overcome. It has been proposed that these electrostatic repulsions take place predominantly through the formation of so-called ion trios in which two ions of like charge interact, on average and at distance, with the same counterion as well as with each other. This model accurately reproduces the experimental patterns of activity and osmotic coefficients exhibited by numerous 3-ion aqueous electrolyte mixtures.Dependence on state parameters
The derivative of an activity coefficient with respect to temperature is related to excess molar enthalpy by : Similarly, the derivative of an activity coefficient with respect to pressure can be related to excess molar volume. :Application to chemical equilibrium
At equilibrium, the sum of the chemical potentials of the reactants is equal to the sum of the chemical potentials of the products. TheGibbs free energy
In thermodynamics, the Gibbs free energy (or Gibbs energy as the recommended name; symbol is a thermodynamic potential that can be used to calculate the maximum amount of Work (thermodynamics), work, other than Work (thermodynamics)#Pressure–v ...
change for the reactions, Δr''G'', is equal to the difference between these sums and therefore, at equilibrium, is equal to zero. Thus, for an equilibrium such as
:
:
Substitute in the expressions for the chemical potential of each reactant:
:
Upon rearrangement this expression becomes
:
The sum
is the standard free energy change for the reaction, .
Therefore,
:
where is the equilibrium constant
The equilibrium constant of a chemical reaction is the value of its reaction quotient at chemical equilibrium, a state approached by a dynamic chemical system after sufficient time has elapsed at which its composition has no measurable tendency ...
. Note that activities and equilibrium constants are dimensionless numbers.
This derivation serves two purposes. It shows the relationship between standard free energy change and equilibrium constant. It also shows that an equilibrium constant is defined as a quotient of activities. In practical terms this is inconvenient. When each activity is replaced by the product of a concentration and an activity coefficient, the equilibrium constant is defined as
:
where denotes the concentration
In chemistry, concentration is the abundance of a constituent divided by the total volume of a mixture. Several types of mathematical description can be distinguished: '' mass concentration'', '' molar concentration'', '' number concentration'', ...
of S, etc. In practice equilibrium constants are determined in a medium such that the quotient of activity coefficients is constant and can be ignored, leading to the usual expression
:
which applies under the conditions that the activity quotient has a particular (constant) value.
References
External links
AIOMFAC online-model
An interactive group-contribution model for the calculation of activity coefficients in organic–inorganic mixtures.
''Electrochimica Acta''
Single-ion activity coefficients {{DEFAULTSORT:Activity Coefficient Thermodynamic models Equilibrium chemistry Dimensionless numbers of chemistry