832 Symmetry on:
[Wikipedia]
[Google]
[Amazon]
In
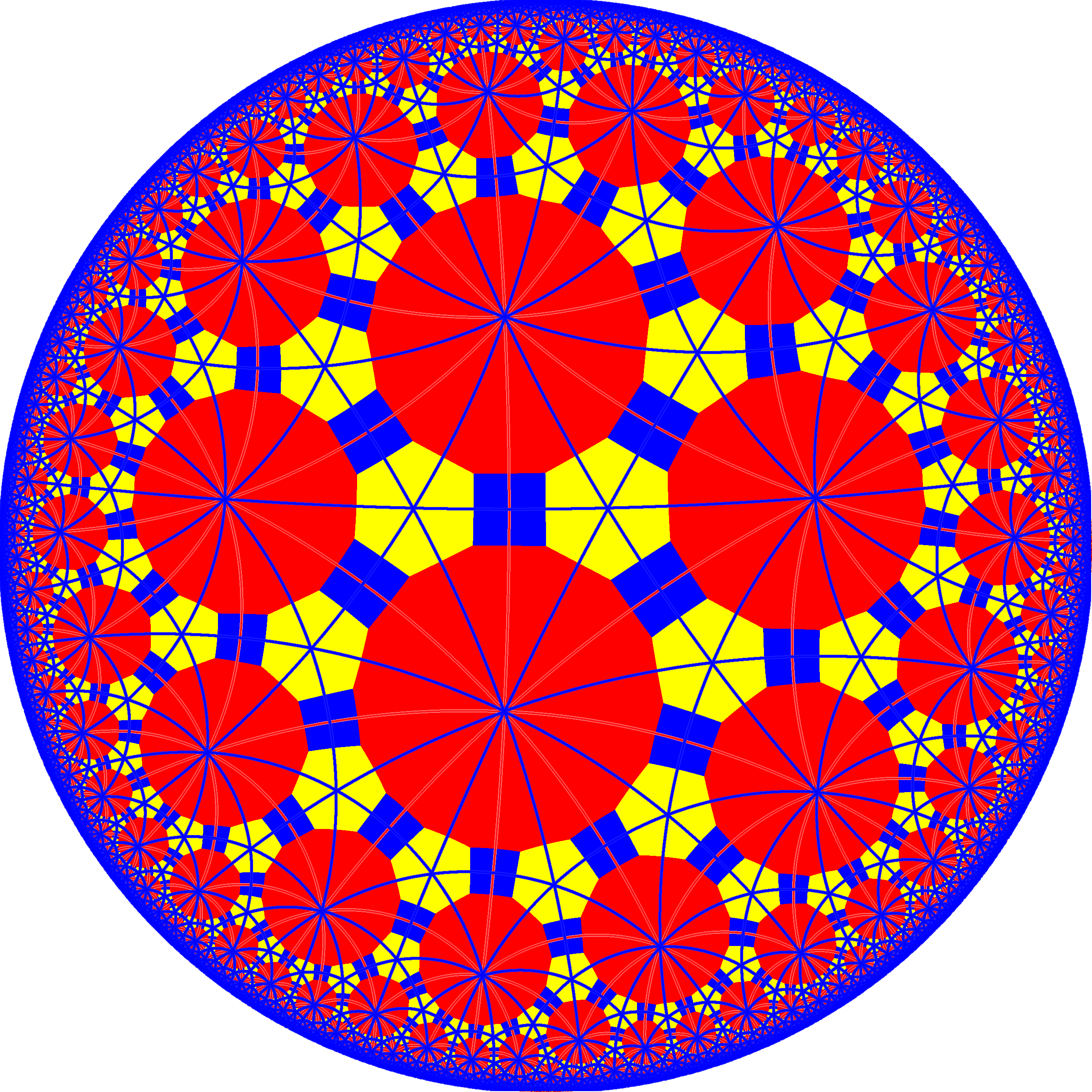 The dual of this tiling, the order 3-8 kisrhombille, represents the fundamental domains of ,3(*832) symmetry. There are 3 small index subgroups constructed from ,3by mirror removal and alternation. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors.
A larger index 6 subgroup constructed as ,3* becomes 4,4,4) (*444). An intermediate index 3 subgroup is constructed as ,3⅄ with 2/3 of blue mirrors removed.
The dual of this tiling, the order 3-8 kisrhombille, represents the fundamental domains of ,3(*832) symmetry. There are 3 small index subgroups constructed from ,3by mirror removal and alternation. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors.
A larger index 6 subgroup constructed as ,3* becomes 4,4,4) (*444). An intermediate index 3 subgroup is constructed as ,3⅄ with 2/3 of blue mirrors removed.
Hyperbolic and Spherical Tiling Gallery
* ttp://www.hadron.org/~hatch/HyperbolicTesselations Hyperbolic Planar Tessellations, Don Hatch {{Tessellation Hyperbolic tilings Isogonal tilings Semiregular tilings Truncated tilings
geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, the truncated trioctagonal tiling is a semiregular tiling of the hyperbolic plane. There are one square
In geometry, a square is a regular polygon, regular quadrilateral. It has four straight sides of equal length and four equal angles. Squares are special cases of rectangles, which have four equal angles, and of rhombuses, which have four equal si ...
, one hexagon
In geometry, a hexagon (from Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.
Regular hexagon
A regular hexagon is de ...
, and one hexadecagon
In mathematics, a hexadecagon (sometimes called a hexakaidecagon or 16-gon) is a sixteen-sided polygon.
Regular hexadecagon
A ''regular polygon, regular hexadecagon'' is a hexadecagon in which all angles are equal and all sides are congruent. It ...
(16-sides) on each vertex. It has Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines List of regular polytopes and compounds, regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, wh ...
of ''tr''.
Symmetry
 The dual of this tiling, the order 3-8 kisrhombille, represents the fundamental domains of ,3(*832) symmetry. There are 3 small index subgroups constructed from ,3by mirror removal and alternation. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors.
A larger index 6 subgroup constructed as ,3* becomes 4,4,4) (*444). An intermediate index 3 subgroup is constructed as ,3⅄ with 2/3 of blue mirrors removed.
The dual of this tiling, the order 3-8 kisrhombille, represents the fundamental domains of ,3(*832) symmetry. There are 3 small index subgroups constructed from ,3by mirror removal and alternation. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors.
A larger index 6 subgroup constructed as ,3* becomes 4,4,4) (*444). An intermediate index 3 subgroup is constructed as ,3⅄ with 2/3 of blue mirrors removed.
Order 3-8 kisrhombille
The order 3-8 kisrhombille is a semiregular dual tiling of the hyperbolic plane. It is constructed by congruentright triangle
A right triangle or right-angled triangle, sometimes called an orthogonal triangle or rectangular triangle, is a triangle in which two sides are perpendicular, forming a right angle ( turn or 90 degrees).
The side opposite to the right angle i ...
s with 4, 6, and 16 triangles meeting at each vertex.
The image shows a Poincaré disk model
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of 2-dimensional hyperbolic geometry in which all points are inside the unit disk, and straight lines are either circular arcs contained within the disk t ...
projection of the hyperbolic plane.
It is labeled V4.6.16 because each right triangle face has three types of vertices: one with 4 triangles, one with 6 triangles, and one with 16 triangles. It is the dual tessellation
In geometry, every polyhedron is associated with a second dual structure, where the vertices of one correspond to the faces of the other, and the edges between pairs of vertices of one correspond to the edges between pairs of faces of the other. ...
of the truncated trioctagonal tiling which has one square and one octagon and one hexakaidecagon at each vertex.
Naming
An alternative name is 3-8 kisrhombille byConway
Conway may refer to:
Places
United States
* Conway, Arkansas
* Conway County, Arkansas
* Lake Conway, Arkansas
* Conway, Florida
* Conway, Iowa
* Conway, Kansas
* Conway, Louisiana
* Conway, Massachusetts
* Conway, Michigan
* Conway Townshi ...
, seeing it as a 3-8 rhombic tiling, divided by a kis operator, adding a center point to each rhombus, and dividing into four triangles.
Related polyhedra and tilings
This tiling is one of 10 uniform tilings constructed from ,3hyperbolic symmetry and three subsymmetries +,8,3 ,3+and ,3sup>+. This tiling can be considered a member of a sequence of uniform patterns with vertex figure (4.6.2p) and Coxeter-Dynkin diagram . For ''p'' < 6, the members of the sequence areomnitruncated
In geometry, an omnitruncation of a convex polytope is a simple polytope of the same dimension, having a vertex for each Flag (geometry), flag of the original polytope and a Facet (geometry), facet for each face of any dimension of the original pol ...
polyhedra (zonohedron
In geometry, a zonohedron is a convex polyhedron that is point symmetry, centrally symmetric, every face of which is a polygon that is centrally symmetric (a zonogon). Any zonohedron may equivalently be described as the Minkowski addition, Minkows ...
s), shown below as spherical tilings. For ''p'' > 6, they are tilings of the hyperbolic plane, starting with the truncated triheptagonal tiling.
See also
*Tilings of regular polygons
Euclidean plane tilings by convex regular polygons have been widely used since antiquity. The first systematic mathematical treatment was that of Kepler in his (Latin: ''The Harmony of the World'', 1619).
Notation of Euclidean tilings
Eucl ...
* Hexakis triangular tiling
* List of uniform tilings
This table shows the 11 convex uniform tilings (regular and semiregular) of the Euclidean plane, and their dual tilings.
There are three regular and eight semiregular tilings in the plane. The semiregular tilings form new tilings from their du ...
* Uniform tilings in hyperbolic plane
In hyperbolic geometry, a uniform hyperbolic tiling (or regular, quasiregular or semiregular hyperbolic tiling) is an edge-to-edge filling of the hyperbolic plane which has regular polygons as Face (geometry), faces and is vertex-transitive (Tran ...
References
* John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ''The Symmetries of Things'' 2008, (Chapter 19, The Hyperbolic Archimedean Tessellations) *External links
* *Hyperbolic and Spherical Tiling Gallery
* ttp://www.hadron.org/~hatch/HyperbolicTesselations Hyperbolic Planar Tessellations, Don Hatch {{Tessellation Hyperbolic tilings Isogonal tilings Semiregular tilings Truncated tilings