5-simplex

In five-dimensional geometry, a 5-simplex is a self-dual regular 5-polytope. It has six vertices, 15 edges, 20 triangle faces, 15 tetrahedral cells, and 6 5-cell facets. It has a dihedral angle of cos⁻¹(), or approximately 78.46°.

The 5-simplex is a solution to the problem: ''Make 20 equilateral triangles using 15 matchsticks, where each side of every triangle is exactly one matchstick.''

Alternate names

It can also be called a hexateron, or hexa-5-tope, as a 6- facetted polytope in 5-dimensions. The name ''hexateron'' is derived from ''hexa-'' for having six facets and '' teron'' (with ''ter-'' being a corruption of ''tetra-'') for having four-dimensional facets.

By Jonathan Bowers, a hexateron is given the acronym hix.

As a configuration

This configuration matrix represents the 5-simplex. The rows and columns correspond to vertices, edges, faces, cells and 4-faces. The diagonal numbers say how many of each element occur in the whole 5-simplex. The nondiagonal numbers say how many of the column's element occur in or at the row's element. This self-dual simplex's matrix is identical to its 180 degree rotation.

$\begin\begin6 & 5 & 10 & 10 & 5 \\ 2 & 15 & 4 & 6 & 4 \\ 3 & 3 & 20 & 3 & 3 \\ 4 & 6 & 4 & 15 & 2 \\ 5 & 10 & 10 & 5 & 6 \end\end$

Regular hexateron cartesian coordinates

The ''hexateron'' can be constructed from a 5-cell by adding a 6th vertex such that it is equidistant from all the other vertices of the 5-cell.

The Cartesian coordinates for the vertices of an origin-centered regular hexateron having edge length 2 are:

:\begin
&\left(\tfrac\sqrt,\ \tfrac\sqrt,\ \tfrac\sqrt,\ \tfrac\sqrt,\ \pm1\right)\\ pt&\left(\tfrac\sqrt,\ \tfrac\sqrt,\ \tfrac\sqrt,\ -\tfrac\sqrt,\ 0\right)\\ pt&\left(\tfrac\sqrt,\ \tfrac\sqrt,\ -\tfrac\sqrt\sqrt,\ 0,\ 0\right)\\ pt&\left(\tfrac\sqrt,\ -\tfrac\sqrt,\ 0,\ 0,\ 0\right)\\ pt&\left(-\tfrac\sqrt\sqrt,\ 0,\ 0,\ 0,\ 0\right)
\end

The vertices of the ''5-simplex'' can be more simply positioned on a hyperplane in 6-space as permutations of (0,0,0,0,0,1) ''or'' (0,1,1,1,1,1). These constructions can be seen as facets of the 6-orthoplex or rectified 6-cube respectively.

Projected images

Lower symmetry forms

A lower symmetry form is a ''5-cell pyramid'' ∨( ), with ,3,3symmetry order 120, constructed as a 5-cell base in a 4-space hyperplane, and an apex point ''above'' the hyperplane. The five ''sides'' of the pyramid are made of 5-cell cells. These are seen as vertex figures of truncated regular 6-polytopes, like a truncated 6-cube.

Another form is ∨, with ,3,2,1symmetry order 48, the joining of an orthogonal digon and a tetrahedron, orthogonally offset, with all pairs of vertices connected between. Another form is ∨, with ,2,3,1symmetry order 36, and extended symmetry 3,2,31], order 72. It represents joining of 2 orthogonal triangles, orthogonally offset, with all pairs of vertices connected between.

The form ∨∨ has symmetry ,2,1,1 order 8, extended by permuting 3 segments as [2,21">[2,2.html" ;"title="[2,2">[2,21or [4,3,1,1">[2,2.html"_;"title="[2,2">[2,2<_a>1.html" ;"title="[2,2.html" ;"title="[2,2">[2,21">[2,2.html" ;"title="[2,2">[2,21or [4,3,1,1 order 48.

These are seen in the vertex figures of bitruncated and tritruncated regular 6-polytopes, like a bitruncated 6-cube">Bitruncation">bitruncated and tritruncated regular 6-polytopes, like a bitruncated 6-cube and a tritruncated 6-simplex. The edge labels here represent the types of face along that direction, and thus represent different edge lengths.

The vertex figure of the omnitruncated 5-simplex honeycomb, , is a 5-simplex with a petrie polygon cycle of 5 long edges. Its symmetry is isomorphic to dihedral group Dih₆ or simple rotation group ,2sup>+, order 12.

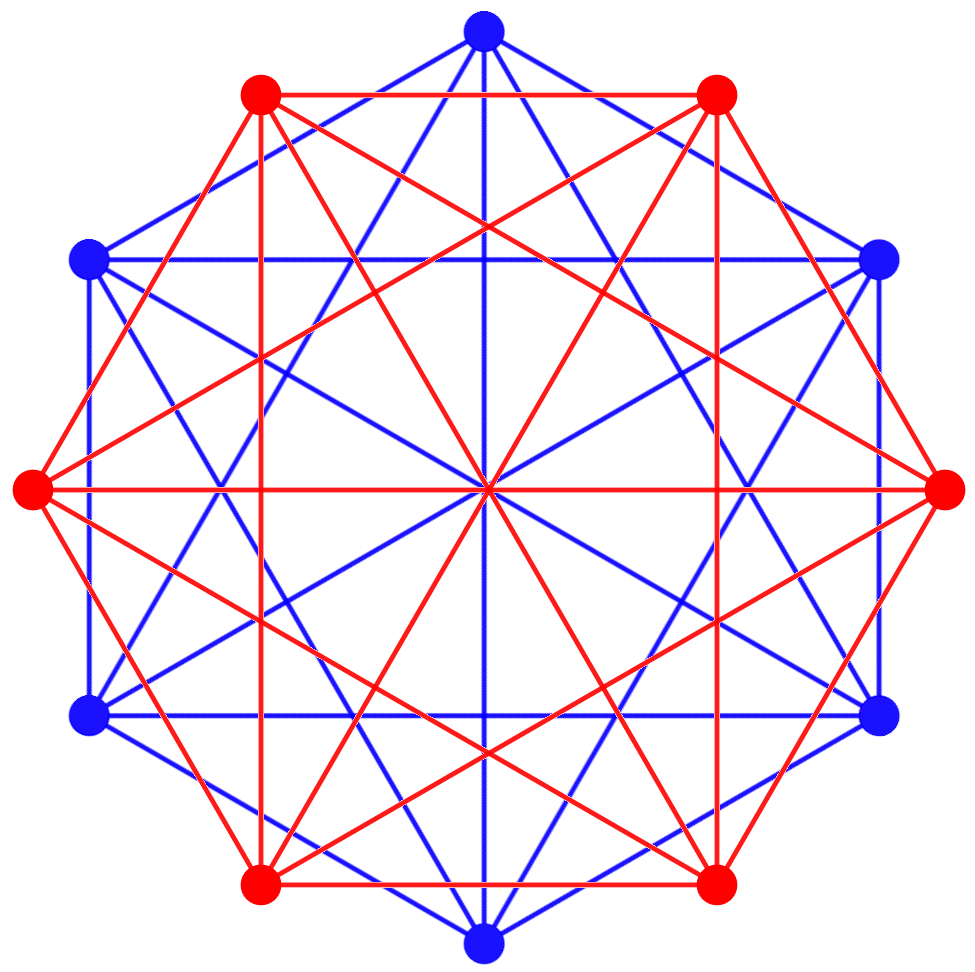
Compound

The compound of two 5-simplexes in dual configurations can be seen in this A6 Coxeter plane projection, with a red and blue 5-simplex vertices and edges. This compound has 3,3,3,3 symmetry, order 1440. The intersection of these two 5-simplexes is a uniform birectified 5-simplex. = ∩ .
:

Related uniform 5-polytopes

It is first in a dimensional series of uniform polytopes and honeycombs, expressed by Coxeter as 1_3k series. A degenerate 4-dimensional case exists as 3-sphere tiling, a tetrahedral hosohedron.

It is first in a dimensional series of uniform polytopes and honeycombs, expressed by Coxeter as 3_k1 series. A degenerate 4-dimensional case exists as 3-sphere tiling, a tetrahedral dihedron.

The 5-simplex, as 2₂₀ polytope is first in dimensional series 2_2k.

The regular 5-simplex is one of 19 uniform polytera based on the ,3,3,3Coxeter group, all shown here in A₅ Coxeter plane orthographic projections. (Vertices are colored by projection overlap order, red, orange, yellow, green, cyan, blue, purple having progressively more vertices)

See also

* 11-cell

Notes

References

*
* Coxeter, H.S.M.:
**
**
*** (Paper 22)
*** (Paper 23)
*** (Paper 24)
*
*
**

External links

*

Polytopes of Various Dimensions
Jonathan Bowers



{{Polytopes

5-polytopes