
In
four-dimensional geometry
Four-dimensional space (4D) is the mathematical extension of the concept of three-dimensional space (3D). Three-dimensional space is the simplest possible abstraction of the observation that one needs only three numbers, called ''dimensions'' ...
, the 24-cell is the convex
regular 4-polytope
In mathematics, a regular 4-polytope or regular polychoron is a regular polytope, regular 4-polytope, four-dimensional polytope. They are the four-dimensional analogues of the Regular polyhedron, regular polyhedra in three dimensions and the regul ...
(four-dimensional analogue of a
Platonic solid
In geometry, a Platonic solid is a Convex polytope, convex, regular polyhedron in three-dimensional space, three-dimensional Euclidean space. Being a regular polyhedron means that the face (geometry), faces are congruence (geometry), congruent (id ...
) with
Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines List of regular polytopes and compounds, regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, wh ...
. It is also called C
24, or the icositetrachoron, octaplex (short for "octahedral complex"), icosatetrahedroid,
octacube, hyper-diamond or polyoctahedron, being constructed of
octahedral
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of i ...
cells.
The boundary of the 24-cell is composed of 24
octahedral
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of i ...
cells with six meeting at each vertex, and three at each edge. Together they have 96 triangular faces, 96 edges, and 24 vertices. The
vertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a general -polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connected ed ...
is a
cube
A cube or regular hexahedron is a three-dimensional space, three-dimensional solid object in geometry, which is bounded by six congruent square (geometry), square faces, a type of polyhedron. It has twelve congruent edges and eight vertices. It i ...
. The 24-cell is
self-dual. The 24-cell and the
tesseract
In geometry, a tesseract or 4-cube is a four-dimensional hypercube, analogous to a two-dimensional square and a three-dimensional cube. Just as the perimeter of the square consists of four edges and the surface of the cube consists of six ...
are the only convex regular 4-polytopes in which the edge length equals the radius.
The 24-cell does not have a regular analogue in
three dimensions
In geometry, a three-dimensional space (3D space, 3-space or, rarely, tri-dimensional space) is a mathematical space in which three values (''coordinates'') are required to determine the position of a point. Most commonly, it is the three-di ...
or any other number of dimensions, either below or above. It is the only one of the six convex regular 4-polytopes which is not the analogue of one of the five Platonic solids. However, it can be seen as the analogue of a pair of irregular solids: the
cuboctahedron
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertex (geometry), vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edge (geometry), edges, each separating a tr ...
and its dual the
rhombic dodecahedron
In geometry, the rhombic dodecahedron is a Polyhedron#Convex_polyhedra, convex polyhedron with 12 congruence (geometry), congruent rhombus, rhombic face (geometry), faces. It has 24 edge (geometry), edges, and 14 vertex (geometry), vertices of 2 ...
.
Translated copies of the 24-cell can
tesselate
A tessellation or tiling is the covering of a surface, often a plane (mathematics), plane, using one or more geometric shapes, called ''tiles'', with no overlaps and no gaps. In mathematics, tessellation can be generalized to high-dimensiona ...
four-dimensional space face-to-face, forming the
24-cell honeycomb. As a polytope that can tile by translation, the 24-cell is an example of a
parallelotope, the simplest one that is not also a
zonotope
In geometry, a zonohedron is a convex polyhedron that is point symmetry, centrally symmetric, every face of which is a polygon that is centrally symmetric (a zonogon). Any zonohedron may equivalently be described as the Minkowski addition, Minkows ...
.
Geometry
The 24-cell incorporates the geometries of every convex regular polytope in the first four dimensions, except the 5-cell, those with a 5 in their Schlӓfli symbol, and the regular polygons with 7 or more sides. In other words, the 24-cell contains ''all'' of the regular polytopes made of triangles and squares that exist in four dimensions except the regular 5-cell, but ''none'' of the pentagonal polytopes. The geometric relationships among all of these regular polytopes can be observed in a single 24-cell or the
24-cell honeycomb.
The 24-cell is the fourth in the sequence of six
convex regular 4-polytope
In mathematics, a regular 4-polytope or regular polychoron is a regular four-dimensional polytope. They are the four-dimensional analogues of the regular polyhedra in three dimensions and the regular polygons in two dimensions.
There are six co ...
s (in order of size and complexity). It can be deconstructed into 3 overlapping instances of its predecessor the
tesseract
In geometry, a tesseract or 4-cube is a four-dimensional hypercube, analogous to a two-dimensional square and a three-dimensional cube. Just as the perimeter of the square consists of four edges and the surface of the cube consists of six ...
(8-cell), as the 8-cell can be deconstructed into 2 instances of its predecessor the
16-cell
In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the ...
. The reverse procedure to construct each of these from an instance of its predecessor preserves the radius of the predecessor, but generally produces a successor with a smaller edge length.
Coordinates
The 24-cell has two natural systems of Cartesian coordinates, which reveal distinct structure.
Squares
The 24-cell is the
convex hull
In geometry, the convex hull, convex envelope or convex closure of a shape is the smallest convex set that contains it. The convex hull may be defined either as the intersection of all convex sets containing a given subset of a Euclidean space, ...
of its vertices which can be described as the 24 coordinate
permutation
In mathematics, a permutation of a set can mean one of two different things:
* an arrangement of its members in a sequence or linear order, or
* the act or process of changing the linear order of an ordered set.
An example of the first mean ...
s of:
Those coordinates can be constructed as ,
rectifying
A rectifier is an electrical device that converts alternating current (AC), which periodically reverses direction, to direct current (DC), which flows in only one direction.
The process is known as ''rectification'', since it "straightens" t ...
the
16-cell
In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the ...
with the 8 vertices that are permutations of (±2,0,0,0). The vertex figure of a 16-cell is the
octahedron
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of i ...
; thus, cutting the vertices of the 16-cell at the midpoint of its incident edges produces 8 octahedral cells. This process also rectifies the tetrahedral cells of the 16-cell which become 16 octahedra, giving the 24-cell 24 octahedral cells.
In this frame of reference the 24-cell has edges of length and is inscribed in a
3-sphere
In mathematics, a hypersphere or 3-sphere is a 4-dimensional analogue of a sphere, and is the 3-dimensional n-sphere, ''n''-sphere. In 4-dimensional Euclidean space, it is the set of points equidistant from a fixed central point. The interior o ...
of radius . Remarkably, the edge length equals the circumradius, as in the
hexagon
In geometry, a hexagon (from Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.
Regular hexagon
A regular hexagon is de ...
, or the
cuboctahedron
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertex (geometry), vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edge (geometry), edges, each separating a tr ...
. Such polytopes are ''radially equilateral''.
The 24 vertices form 18 great squares (3 sets of 6 orthogonal central squares), 3 of which intersect at each vertex. By viewing just one square at each vertex, the 24-cell can be seen as the vertices of 3 pairs of
completely orthogonal great squares which intersect at no vertices.
Hexagons
The 24-cell is
self-dual, having the same number of vertices (24) as cells and the same number of edges (96) as faces.
If the dual of the above 24-cell of edge length is taken by reciprocating it about its ''inscribed'' sphere, another 24-cell is found which has edge length and circumradius 1, and its coordinates reveal more structure. In this frame of reference the 24-cell lies vertex-up, and its vertices can be given as follows:
8 vertices obtained by permuting the ''integer'' coordinates:
and 16 vertices with ''half-integer'' coordinates of the form:
all 24 of which lie at distance 1 from the origin.
Viewed as quaternions, these are the unit
Hurwitz quaternions.
The 24-cell has unit radius and unit edge length in this coordinate system. We refer to the system as ''unit radius coordinates'' to distinguish it from others, such as the radius coordinates used
above
Above may refer to:
*Above (artist)
Tavar Zawacki (b. 1981, California) is a Polish, Portuguese - American abstract artist and
internationally recognized visual artist based in Berlin, Germany. From 1996 to 2016, he created work under the ...
.
The 24 vertices and 96 edges form 16 non-orthogonal great hexagons, four of which intersect at each vertex. By viewing just one hexagon at each vertex, the 24-cell can be seen as the 24 vertices of 4 non-intersecting hexagonal great circles which are
Clifford parallel to each other.
The 12 axes and 16 hexagons of the 24-cell constitute a
Reye configuration, which in the language of
configurations is written as 12
416
3 to indicate that each axis belongs to 4 hexagons, and each hexagon contains 3 axes.
Triangles
The 24 vertices form 32 equilateral great triangles, of edge length in the unit-radius 24-cell, inscribed in the 16 great hexagons. Each great triangle is a ring linking three completely disjoint great squares.
Hypercubic chords

The 24 vertices of the 24-cell are distributed at four different
chord lengths from each other: , , and . The chords (the 24-cell edges) are the edges of central hexagons, and the chords are the diagonals of central hexagons. The chords are the edges of central squares, and the chords are the diagonals of central squares.
Each vertex is joined to 8 others by an edge of length 1, spanning 60° =
of arc. Next nearest are 6 vertices located 90° =
away, along an interior chord of length . Another 8 vertices lie 120° =
away, along an interior chord of length . The opposite vertex is 180° =
away along a diameter of length 2. Finally, as the 24-cell is radially equilateral, its center is 1 edge length away from all vertices.
To visualize how the interior polytopes of the 24-cell fit together (as described
below
Below may refer to:
*Earth
*Ground (disambiguation)
*Soil
*Floor
* Bottom (disambiguation)
*Less than
*Temperatures below freezing
*Hell or underworld
People with the surname
* Ernst von Below (1863–1955), German World War I general
* Fred Belo ...
), keep in mind that the four chord lengths (, , , ) are the long diameters of the
hypercube
In geometry, a hypercube is an ''n''-dimensional analogue of a square ( ) and a cube ( ); the special case for is known as a ''tesseract''. It is a closed, compact, convex figure whose 1- skeleton consists of groups of opposite parallel l ...
s of dimensions 1 through 4: the long diameter of the square is ; the long diameter of the cube is ; and the long diameter of the tesseract is . Moreover, the long diameter of the octahedron is like the square; and the long diameter of the 24-cell itself is like the tesseract.
Geodesics
The vertex chords of the 24-cell are arranged in
geodesic
In geometry, a geodesic () is a curve representing in some sense the locally shortest path ( arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a conn ...
great circle
In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point.
Discussion
Any arc of a great circle is a geodesic of the sphere, so that great circles in spher ...
polygons. The
geodesic distance between two 24-cell vertices along a path of edges is always 1, 2, or 3, and it is 3 only for opposite vertices.
The edges occur in 16
hexagonal great circles (in planes inclined at 60 degrees to each other), 4 of which cross at each vertex. The 96 distinct edges divide the surface into 96 triangular faces and 24 octahedral cells: a 24-cell. The 16 hexagonal great circles can be divided into 4 sets of 4 non-intersecting
Clifford parallel geodesics, such that only one hexagonal great circle in each set passes through each vertex, and the 4 hexagons in each set reach all 24 vertices.
The chords occur in 18
square great circles (3 sets of 6 orthogonal planes), 3 of which cross at each vertex. The 72 distinct chords do not run in the same planes as the hexagonal great circles; they do not follow the 24-cell's edges, they pass through its octagonal cell centers. The 72 chords are the 3 orthogonal axes of the 24 octahedral cells, joining vertices which are 2 edges apart. The 18 square great circles can be divided into 3 sets of 6 non-intersecting Clifford parallel geodesics, such that only one square great circle in each set passes through each vertex, and the 6 squares in each set reach all 24 vertices.
The chords occur in 32
triangular great circles in 16 planes, 4 of which cross at each vertex. The 96 distinct chords run vertex-to-every-other-vertex in the same planes as the hexagonal great circles. They are the 3 edges of the 32 great triangles inscribed in the 16 great hexagons, joining vertices which are 2 edges apart on a great circle.
The chords occur as 12 vertex-to-vertex diameters (3 sets of 4 orthogonal axes), the 24 radii around the 25th central vertex.
The sum of the squared lengths of all these distinct chords of the 24-cell is 576 = 24
2. These are all the central polygons through vertices, but in 4-space there are geodesics on the 3-sphere which do not lie in central planes at all. There are geodesic shortest paths between two 24-cell vertices that are helical rather than simply circular; they correspond to diagonal
isoclinic rotations rather than
simple rotations.
The edges occur in 48 parallel pairs, apart. The chords occur in 36 parallel pairs, apart. The chords occur in 48 parallel pairs, apart.
The central planes of the 24-cell can be divided into 4 orthogonal central hyperplanes (3-spaces) each forming a
cuboctahedron
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertex (geometry), vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edge (geometry), edges, each separating a tr ...
. The great hexagons are 60 degrees apart; the great squares are 90 degrees or 60 degrees apart; a great square and a great hexagon are 90 degrees ''and'' 60 degrees apart. Each set of similar central polygons (squares or hexagons) can be divided into 4 sets of non-intersecting Clifford parallel polygons (of 6 squares or 4 hexagons). Each set of Clifford parallel great circles is a parallel
fiber bundle
In mathematics, and particularly topology, a fiber bundle ( ''Commonwealth English'': fibre bundle) is a space that is a product space, but may have a different topological structure. Specifically, the similarity between a space E and a pr ...
which visits all 24 vertices just once.
Each great circle intersects with the other great circles to which it is not Clifford parallel at one diameter of the 24-cell. Great circles which are
completely orthogonal or otherwise Clifford parallel do not intersect at all: they pass through disjoint sets of vertices.
Constructions
Triangles and squares come together uniquely in the 24-cell to generate, as interior features, all of the triangle-faced and square-faced regular convex polytopes in the first four dimensions (with caveats for the
5-cell
In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol . It is a 5-vertex four-dimensional space, four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, hypertetrahedron, pentachoron, pentatope, pe ...
and the
600-cell
In geometry, the 600-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol .
It is also known as the C600, hexacosichoron and hexacosihedroid.
It is also called a tetraplex (abbreviated from ...
). Consequently, there are numerous ways to construct or deconstruct the 24-cell.
Reciprocal constructions from 8-cell and 16-cell
The 8 integer vertices (±1, 0, 0, 0) are the vertices of a regular
16-cell
In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the ...
, and the 16 half-integer vertices (±, ±, ±, ±) are the vertices of its dual, the
tesseract
In geometry, a tesseract or 4-cube is a four-dimensional hypercube, analogous to a two-dimensional square and a three-dimensional cube. Just as the perimeter of the square consists of four edges and the surface of the cube consists of six ...
(8-cell). The tesseract gives Gosset's construction of the 24-cell, equivalent to cutting a tesseract into 8
cubic pyramids, and then attaching them to the facets of a second tesseract. The analogous construction in 3-space gives the
rhombic dodecahedron
In geometry, the rhombic dodecahedron is a Polyhedron#Convex_polyhedra, convex polyhedron with 12 congruence (geometry), congruent rhombus, rhombic face (geometry), faces. It has 24 edge (geometry), edges, and 14 vertex (geometry), vertices of 2 ...
which, however, is not regular. The 16-cell gives the reciprocal construction of the 24-cell, Cesaro's construction, equivalent to rectifying a 16-cell (truncating its corners at the mid-edges, as described
above
Above may refer to:
*Above (artist)
Tavar Zawacki (b. 1981, California) is a Polish, Portuguese - American abstract artist and
internationally recognized visual artist based in Berlin, Germany. From 1996 to 2016, he created work under the ...
). The analogous construction in 3-space gives the
cuboctahedron
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertex (geometry), vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edge (geometry), edges, each separating a tr ...
(dual of the rhombic dodecahedron) which, however, is not regular. The tesseract and the 16-cell are the only regular 4-polytopes in the 24-cell.
We can further divide the 16 half-integer vertices into two groups: those whose coordinates contain an even number of minus (−) signs and those with an odd number. Each of these groups of 8 vertices also define a regular 16-cell. This shows that the vertices of the 24-cell can be grouped into three disjoint sets of eight with each set defining a regular 16-cell, and with the complement defining the dual tesseract. This also shows that the symmetries of the 16-cell form a subgroup of index 3 of the symmetry group of the 24-cell.
Diminishings
We can
facet
Facets () are flat faces on geometric shapes. The organization of naturally occurring facets was key to early developments in crystallography, since they reflect the underlying symmetry of the crystal structure. Gemstones commonly have facets cu ...
the 24-cell by cutting through interior cells bounded by vertex chords to remove vertices, exposing the
facets of interior 4-polytopes
inscribed
An inscribed triangle of a circle
In geometry, an inscribed planar shape or solid is one that is enclosed by and "fits snugly" inside another geometric shape or solid. To say that "figure F is inscribed in figure G" means precisely the same th ...
in the 24-cell. One can cut a 24-cell through any planar hexagon of 6 vertices, any planar rectangle of 4 vertices, or any triangle of 3 vertices. The great circle central planes (
above
Above may refer to:
*Above (artist)
Tavar Zawacki (b. 1981, California) is a Polish, Portuguese - American abstract artist and
internationally recognized visual artist based in Berlin, Germany. From 1996 to 2016, he created work under the ...
) are only some of those planes. Here we shall expose some of the others: the face planes of interior polytopes.
= 8-cell
=
Starting with a complete 24-cell, remove 8 orthogonal vertices (4 opposite pairs on 4 perpendicular axes), and the 8 edges which radiate from each, by cutting through 8 cubic cells bounded by edges to remove 8
cubic pyramids whose
apexes are the vertices to be removed. This removes 4 edges from each hexagonal great circle (retaining just one opposite pair of edges), so no continuous hexagonal great circles remain. Now 3 perpendicular edges meet and form the corner of a cube at each of the 16 remaining vertices, and the 32 remaining edges divide the surface into 24 square faces and 8 cubic cells: a
tesseract
In geometry, a tesseract or 4-cube is a four-dimensional hypercube, analogous to a two-dimensional square and a three-dimensional cube. Just as the perimeter of the square consists of four edges and the surface of the cube consists of six ...
. There are three ways you can do this (choose a set of 8 orthogonal vertices out of 24), so there are three such tesseracts inscribed in the 24-cell. They overlap with each other, but most of their element sets are disjoint: they share some vertex count, but no edge length, face area, or cell volume. They do share 4-content, their common core.
= 16-cell
=
Starting with a complete 24-cell, remove the 16 vertices of a tesseract (retaining the 8 vertices you removed above), by cutting through 16 tetrahedral cells bounded by chords to remove 16
tetrahedral pyramids whose apexes are the vertices to be removed. This removes 12 great squares (retaining just one orthogonal set) and all the edges, exposing chords as the new edges. Now the remaining 6 great squares cross perpendicularly, 3 at each of 8 remaining vertices, and their 24 edges divide the surface into 32 triangular faces and 16 tetrahedral cells: a
16-cell
In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the ...
. There are three ways you can do this (remove 1 of 3 sets of tesseract vertices), so there are three such 16-cells inscribed in the 24-cell. They overlap with each other, but all of their element sets are disjoint: they do not share any vertex count, edge length, or face area, but they do share cell volume. They also share 4-content, their common core.
Tetrahedral constructions
The 24-cell can be constructed radially from 96 equilateral triangles of edge length which meet at the center of the polytope, each contributing two radii and an edge. They form 96 tetrahedra (each contributing one 24-cell face), all sharing the 25th central apex vertex. These form 24 octahedral pyramids (half-16-cells) with their apexes at the center.
The 24-cell can be constructed from 96 equilateral triangles of edge length , where the three vertices of each triangle are located 90° =
away from each other on the 3-sphere. They form 48 -edge tetrahedra (the cells of the
three 16-cells), centered at the 24 mid-edge-radii of the 24-cell.
The 24-cell can be constructed directly from its
characteristic simplex , the
irregular 5-cell which is the
fundamental region of its
symmetry group
In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the amb ...
F4, by reflection of that 4-
orthoscheme in its own cells (which are 3-orthoschemes).
Cubic constructions
The 24-cell is not only the 24-octahedral-cell, it is also the 24-cubical-cell, although the cubes are cells of the three 8-cells, not cells of the 24-cell, in which they are not volumetrically disjoint.
The 24-cell can be constructed from 24 cubes of its own edge length (three 8-cells). Each of the cubes is shared by 2 8-cells, each of the cubes' square faces is shared by 4 cubes (in 2 8-cells), each of the 96 edges is shared by 8 square faces (in 4 cubes in 2 8-cells), and each of the 96 vertices is shared by 16 edges (in 8 square faces in 4 cubes in 2 8-cells).
Relationships among interior polytopes
The 24-cell, three tesseracts, and three 16-cells are deeply entwined around their common center, and intersect in a common core. The tesseracts and the 16-cells are rotated 60° isoclinically with respect to each other. This means that the corresponding vertices of two tesseracts or two 16-cells are (120°) apart.
The tesseracts are inscribed in the 24-cell such that their vertices and edges are exterior elements of the 24-cell, but their square faces and cubical cells lie inside the 24-cell (they are not elements of the 24-cell). The 16-cells are inscribed in the 24-cell such that only their vertices are exterior elements of the 24-cell: their edges, triangular faces, and tetrahedral cells lie inside the 24-cell. The interior 16-cell edges have length .
The 16-cells are also inscribed in the tesseracts: their edges are the face diagonals of the tesseract, and their 8 vertices occupy every other vertex of the tesseract. Each tesseract has two 16-cells inscribed in it (occupying the opposite vertices and face diagonals), so each 16-cell is inscribed in two of the three 8-cells. This is reminiscent of the way, in 3 dimensions, two opposing regular tetrahedra can be inscribed in a cube, as discovered by Kepler. In fact it is the exact dimensional analogy (the
demihypercubes), and the 48 tetrahedral cells are inscribed in the 24 cubical cells in just that way.
The 24-cell encloses the three tesseracts within its envelope of octahedral facets, leaving 4-dimensional space in some places between its envelope and each tesseract's envelope of cubes. Each tesseract encloses two of the three 16-cells, leaving 4-dimensional space in some places between its envelope and each 16-cell's envelope of tetrahedra. Thus there are measurable 4-dimensional interstices between the 24-cell, 8-cell and 16-cell envelopes. The shapes filling these gaps are
4-pyramids, alluded to above.
Boundary cells
Despite the 4-dimensional interstices between 24-cell, 8-cell and 16-cell envelopes, their 3-dimensional volumes overlap. The different envelopes are separated in some places, and in contact in other places (where no 4-pyramid lies between them). Where they are in contact, they merge and share cell volume: they are the same 3-membrane in those places, not two separate but adjacent 3-dimensional layers. Because there are a total of 7 envelopes, there are places where several envelopes come together and merge volume, and also places where envelopes interpenetrate (cross from inside to outside each other).
Some interior features lie within the 3-space of the (outer) boundary envelope of the 24-cell itself: each octahedral cell is bisected by three perpendicular squares (one from each of the tesseracts), and the diagonals of those squares (which cross each other perpendicularly at the center of the octahedron) are 16-cell edges (one from each 16-cell). Each square bisects an octahedron into two square pyramids, and also bonds two adjacent cubic cells of a tesseract together as their common face.
As we saw
above
Above may refer to:
*Above (artist)
Tavar Zawacki (b. 1981, California) is a Polish, Portuguese - American abstract artist and
internationally recognized visual artist based in Berlin, Germany. From 1996 to 2016, he created work under the ...
, 16-cell tetrahedral cells are inscribed in tesseract cubic cells, sharing the same volume. 24-cell octahedral cells overlap their volume with cubic cells: they are bisected by a square face into two square pyramids, the apexes of which also lie at a vertex of a cube. The octahedra share volume not only with the cubes, but with the tetrahedra inscribed in them; thus the 24-cell, tesseracts, and 16-cells all share some boundary volume.
As a configuration
This
configuration matrix represents the 24-cell. The rows and columns correspond to vertices, edges, faces, and cells. The diagonal numbers say how many of each element occur in the whole 24-cell. The non-diagonal numbers say how many of the column's element occur in or at the row's element.
Since the 24-cell is self-dual, its matrix is identical to its 180 degree rotation.
Symmetries, root systems, and tessellations

The 24 root vectors of the
D4 root system of the
simple Lie group
In mathematics, a simple Lie group is a connected non-abelian Lie group ''G'' which does not have nontrivial connected normal subgroups. The list of simple Lie groups can be used to read off the list of simple Lie algebras and Riemannian symm ...
SO(8) form the vertices of a 24-cell. The vertices can be seen in 3
hyperplane
In geometry, a hyperplane is a generalization of a two-dimensional plane in three-dimensional space to mathematical spaces of arbitrary dimension. Like a plane in space, a hyperplane is a flat hypersurface, a subspace whose dimension is ...
s, with the 6 vertices of an
octahedron
In geometry, an octahedron (: octahedra or octahedrons) is any polyhedron with eight faces. One special case is the regular octahedron, a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Many types of i ...
cell on each of the outer hyperplanes and 12 vertices of a
cuboctahedron
A cuboctahedron is a polyhedron with 8 triangular faces and 6 square faces. A cuboctahedron has 12 identical vertex (geometry), vertices, with 2 triangles and 2 squares meeting at each, and 24 identical edge (geometry), edges, each separating a tr ...
on a central hyperplane. These vertices, combined with the 8 vertices of the
16-cell
In geometry, the 16-cell is the regular convex 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is one of the six regular convex 4-polytopes first described by the Swiss mathematician Ludwig Schläfli in the ...
, represent the 32 root vectors of the B
4 and C
4 simple Lie groups.
The 48 vertices (or strictly speaking their radius vectors) of the union of the 24-cell and its dual form the
root system
In mathematics, a root system is a configuration of vector space, vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras, especially the classification and ...
of type
F4. The 24 vertices of the original 24-cell form a root system of type D
4; its size has the ratio :1. This is likewise true for the 24 vertices of its dual. The full
symmetry group
In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the amb ...
of the 24-cell is the
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group (named after Hermann Weyl) of a root system Φ is a subgroup of the isometry group of that root system. Specifically, it is the subgroup which is generated by reflections t ...
of F
4, which is generated by
reflections through the hyperplanes orthogonal to the F
4 roots. This is a
solvable group
In mathematics, more specifically in the field of group theory, a solvable group or soluble group is a group that can be constructed from abelian groups using extensions. Equivalently, a solvable group is a group whose derived series terminat ...
of order 1152. The rotational symmetry group of the 24-cell is of order 576.
Quaternionic interpretation
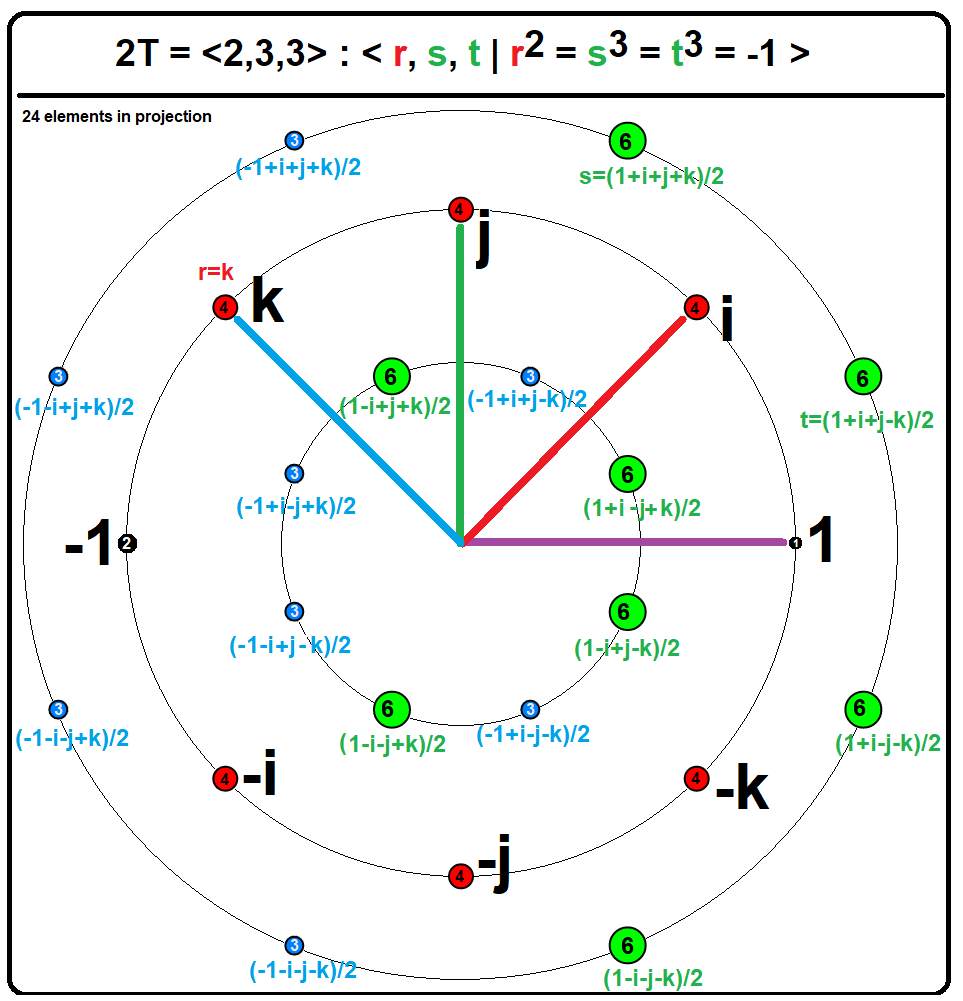
When interpreted as the
quaternion
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quater ...
s, the F
4 root lattice (which is the integral span of the vertices of the 24-cell) is closed under multiplication and is therefore a
ring
(The) Ring(s) may refer to:
* Ring (jewellery), a round band, usually made of metal, worn as ornamental jewelry
* To make a sound with a bell, and the sound made by a bell
Arts, entertainment, and media Film and TV
* ''The Ring'' (franchise), a ...
. This is the ring of
Hurwitz integral quaternions. The vertices of the 24-cell form the
group of units
In algebra, a unit or invertible element of a ring is an invertible element for the multiplication of the ring. That is, an element of a ring is a unit if there exists in such that
vu = uv = 1,
where is the multiplicative identity; the ele ...
(i.e. the group of invertible elements) in the Hurwitz quaternion ring (this group is also known as the
binary tetrahedral group
In mathematics, the binary tetrahedral group, denoted 2T or ,Coxeter&Moser: Generators and Relations for discrete groups: : Rl = Sm = Tn = RST is a certain nonabelian group of order (group theory), order 24. It is an group extension, extension of ...
). The vertices of the 24-cell are precisely the 24 Hurwitz quaternions with norm squared 1, and the vertices of the dual 24-cell are those with norm squared 2. The D
4 root lattice is the
dual of the F
4 and is given by the subring of Hurwitz quaternions with even norm squared.
Viewed as the 24 unit
Hurwitz quaternion
In mathematics, a Hurwitz quaternion (or Hurwitz integer) is a quaternion whose components are ''either'' all integers ''or'' all half-integers (halves of odd integers; a mixture of integers and half-integers is excluded). The set of all Hurwitz ...
s, the
unit radius coordinates of the 24-cell represent (in antipodal pairs) the 12 rotations of a regular tetrahedron.
Vertices of other
convex regular 4-polytope
In mathematics, a regular 4-polytope or regular polychoron is a regular four-dimensional polytope. They are the four-dimensional analogues of the regular polyhedra in three dimensions and the regular polygons in two dimensions.
There are six co ...
s also form multiplicative groups of quaternions, but few of them generate a root lattice.
Voronoi cells
The
Voronoi cell
In mathematics, a Voronoi diagram is a partition of a plane into regions close to each of a given set of objects. It can be classified also as a tessellation. In the simplest case, these objects are just finitely many points in the plane (calle ...
s of the
D4 root lattice are regular 24-cells. The corresponding Voronoi tessellation gives the
tessellation
A tessellation or tiling is the covering of a surface, often a plane, using one or more geometric shapes, called ''tiles'', with no overlaps and no gaps. In mathematics, tessellation can be generalized to higher dimensions and a variety ...
of 4-dimensional
Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
by regular 24-cells, the
24-cell honeycomb. The 24-cells are centered at the D
4 lattice points (Hurwitz quaternions with even norm squared) while the vertices are at the F
4 lattice points with odd norm squared. Each 24-cell of this tessellation has 24 neighbors. With each of these it shares an octahedron. It also has 24 other neighbors with which it shares only a single vertex. Eight 24-cells meet at any given vertex in this tessellation. The
Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines List of regular polytopes and compounds, regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, wh ...
for this tessellation is . It is one of only three regular tessellations of R
4.
The unit
balls inscribed in the 24-cells of this tessellation give rise to the densest known
lattice packing of
hypersphere
In mathematics, an -sphere or hypersphere is an - dimensional generalization of the -dimensional circle and -dimensional sphere to any non-negative integer .
The circle is considered 1-dimensional and the sphere 2-dimensional because a point ...
s in 4 dimensions. The vertex configuration of the 24-cell has also been shown to give the
highest possible kissing number in 4 dimensions.
Radially equilateral honeycomb
The dual tessellation of the
24-cell honeycomb is the
16-cell honeycomb . The third regular tessellation of four dimensional space is the
tesseractic honeycomb , whose vertices can be described by 4-integer Cartesian coordinates. The congruent relationships among these three tessellations can be helpful in visualizing the 24-cell, in particular the radial equilateral symmetry which it shares with the tesseract.
A honeycomb of unit edge length 24-cells may be overlaid on a honeycomb of unit edge length tesseracts such that every vertex of a tesseract (every 4-integer coordinate) is also the vertex of a 24-cell (and tesseract edges are also 24-cell edges), and every center of a 24-cell is also the center of a tesseract. The 24-cells are twice as large as the tesseracts by 4-dimensional content (hypervolume), so overall there are two tesseracts for every 24-cell, only half of which are inscribed in a 24-cell. If those tesseracts are colored black, and their adjacent tesseracts (with which they share a cubical facet) are colored red, a 4-dimensional checkerboard results. Of the 24 center-to-vertex radii of each 24-cell, 16 are also the radii of a black tesseract inscribed in the 24-cell. The other 8 radii extend outside the black tesseract (through the centers of its cubical facets) to the centers of the 8 adjacent red tesseracts. Thus the 24-cell honeycomb and the tesseractic honeycomb coincide in a special way: 8 of the 24 vertices of each 24-cell do not occur at a vertex of a tesseract (they occur at the center of a tesseract instead). Each black tesseract is cut from a 24-cell by truncating it at these 8 vertices, slicing off 8 cubic pyramids (as in reversing Gosset's construction, but instead of being removed the pyramids are simply colored red and left in place). Eight 24-cells meet at the center of each red tesseract: each one meets its opposite at that shared vertex, and the six others at a shared octahedral cell.
The red tesseracts are filled cells (they contain a central vertex and radii); the black tesseracts are empty cells. The vertex set of this union of two honeycombs includes the vertices of all the 24-cells and tesseracts, plus the centers of the red tesseracts. Adding the 24-cell centers (which are also the black tesseract centers) to this honeycomb yields a 16-cell honeycomb, the vertex set of which includes all the vertices and centers of all the 24-cells and tesseracts. The formerly empty centers of adjacent 24-cells become the opposite vertices of a unit edge length 16-cell. 24 half-16-cells (octahedral pyramids) meet at each formerly empty center to fill each 24-cell, and their octahedral bases are the 6-vertex octahedral facets of the 24-cell (shared with an adjacent 24-cell).
Notice the complete absence of pentagons anywhere in this union of three honeycombs. Like the 24-cell, 4-dimensional Euclidean space itself is entirely filled by a complex of all the polytopes that can be built out of regular triangles and squares (except the 5-cell), but that complex does not require (or permit) any of the pentagonal polytopes.
Rotations

The
regular convex 4-polytopes are an
expression of their underlying
symmetry
Symmetry () in everyday life refers to a sense of harmonious and beautiful proportion and balance. In mathematics, the term has a more precise definition and is usually used to refer to an object that is Invariant (mathematics), invariant und ...
which is known as
SO(4)
In mathematics, the group (mathematics), group of rotations about a fixed point in four-dimensional space, four-dimensional Euclidean space is denoted SO(4). The name comes from the fact that it is the special orthogonal group of order 4.
In this ...
, the
group
A group is a number of persons or things that are located, gathered, or classed together.
Groups of people
* Cultural group, a group whose members share the same cultural identity
* Ethnic group, a group whose members share the same ethnic iden ...
of rotations about a fixed point in 4-dimensional Euclidean space.
The 3 Cartesian bases of the 24-cell
There are three distinct orientations of the tesseractic honeycomb which could be made to coincide with the 24-cell
honeycomb
A honeycomb is a mass of Triangular prismatic honeycomb#Hexagonal prismatic honeycomb, hexagonal prismatic cells built from beeswax by honey bees in their beehive, nests to contain their brood (eggs, larvae, and pupae) and stores of honey and pol ...
, depending on which of the 24-cell's three disjoint sets of 8 orthogonal vertices (which set of 4 perpendicular axes, or equivalently, which inscribed basis 16-cell) was chosen to align it, just as three tesseracts can be inscribed in the 24-cell, rotated with respect to each other. The distance from one of these orientations to another is an
isoclinic rotation through 60 degrees (a
double rotation
In mathematics, the group of rotations about a fixed point in four-dimensional Euclidean space is denoted SO(4). The name comes from the fact that it is the special orthogonal group of order 4.
In this article ''rotation'' means ''rotational dis ...
of 60 degrees in each pair of orthogonal invariant planes, around a single fixed point). This rotation can be seen most clearly in the hexagonal central planes, where every hexagon rotates to change which of its three diameters is aligned with a coordinate system axis.
Planes of rotation
Rotations in 4-dimensional Euclidean space can be seen as the composition of two 2-dimensional rotations in completely orthogonal planes. Thus the general rotation in 4-space is a ''double rotation''. There are two important special cases, called a ''simple rotation'' and an ''isoclinic rotation''.
Simple rotations
In 3 dimensions a spinning polyhedron has a single invariant central ''plane of rotation''. The plane is an
invariant set because each point in the plane moves in a circle but stays within the plane. Only ''one'' of a polyhedron's central planes can be invariant during a particular rotation; the choice of invariant central plane, and the angular distance and direction it is rotated, completely specifies the rotation. Points outside the invariant plane also move in circles (unless they are on the fixed ''axis of rotation'' perpendicular to the invariant plane), but the circles do not lie within a
''central'' plane.
When a 4-polytope is rotating with only one invariant central plane, the same kind of
simple rotation is happening that occurs in 3 dimensions. One difference is that instead of a fixed axis of rotation, there is an entire fixed central plane in which the points do not move. The fixed plane is the one central plane that is
completely orthogonal to the invariant plane of rotation. In the 24-cell, there is a simple rotation which will take any vertex ''directly'' to any other vertex, also moving most of the other vertices but leaving at least 2 and at most 6 other vertices fixed (the vertices that the fixed central plane intersects). The vertex moves along a great circle in the invariant plane of rotation between adjacent vertices of a great hexagon, a great square or a great
digon
In geometry, a bigon, digon, or a ''2''-gon, is a polygon with two sides (edge (geometry), edges) and two Vertex (geometry), vertices. Its construction is Degeneracy (mathematics), degenerate in a Euclidean plane because either the two sides wou ...
, and the completely orthogonal fixed plane is a digon, a square or a hexagon, respectively.
Double rotations
The points in the completely orthogonal central plane are not ''constrained'' to be fixed. It is also possible for them to be rotating in circles, as a second invariant plane, at a rate independent of the first invariant plane's rotation: a
double rotation
In mathematics, the group of rotations about a fixed point in four-dimensional Euclidean space is denoted SO(4). The name comes from the fact that it is the special orthogonal group of order 4.
In this article ''rotation'' means ''rotational dis ...
in two perpendicular non-intersecting planes of rotation at once. In a double rotation there is no fixed plane or axis: every point moves except the center point. The angular distance rotated may be different in the two completely orthogonal central planes, but they are always both invariant: their circularly moving points remain within the plane ''as the whole plane tilts sideways'' in the completely orthogonal rotation. A rotation in 4-space always has (at least) ''two'' completely orthogonal invariant planes of rotation, although in a simple rotation the angle of rotation in one of them is 0.
Double rotations come in two
chiral
Chirality () is a property of asymmetry important in several branches of science. The word ''chirality'' is derived from the Greek language, Greek (''kheir''), "hand", a familiar chiral object.
An object or a system is ''chiral'' if it is dist ...
forms: ''left'' and ''right'' rotations. In a double rotation each vertex moves in a spiral along two orthogonal great circles at once. Either the path is right-hand
threaded (like most screws and bolts), moving along the circles in the "same" directions, or it is left-hand threaded (like a reverse-threaded bolt), moving along the circles in what we conventionally say are "opposite" directions (according to the
right hand rule by which we conventionally say which way is "up" on each of the 4 coordinate axes).
In double rotations of the 24-cell that take vertices to vertices, one invariant plane of rotation contains either a great hexagon, a great square, or only an axis (two vertices, a great digon). The completely orthogonal invariant plane of rotation will necessarily contain a great digon, a great square, or a great hexagon, respectively. The selection of an invariant plane of rotation, a rotational direction and angle through which to rotate it, and a rotational direction and angle through which to rotate its completely orthogonal plane, completely determines the nature of the rotational displacement. In the 24-cell there are several noteworthy kinds of double rotation permitted by these parameters.
Isoclinic rotations
When the angles of rotation in the two completely orthogonal invariant planes are exactly the same, a
remarkably symmetric transformation occurs: all the great circle planes Clifford parallel to the pair of invariant planes become pairs of invariant planes of rotation themselves, through that same angle, and the 4-polytope rotates
isoclinically in many directions at once. Each vertex moves an equal distance in four orthogonal directions at the same time. In the 24-cell any isoclinic rotation through 60 degrees in a hexagonal plane takes each vertex to a vertex two edge lengths away, rotates ''all 16'' hexagons by 60 degrees, and takes ''every'' great circle polygon (square, hexagon or triangle) to a Clifford parallel great circle polygon of the same kind 120 degrees away. An isoclinic rotation is also called a ''Clifford displacement'', after its
discoverer.
The 24-cell in the ''double'' rotation animation appears to turn itself inside out. It appears to, because it actually does, reversing the
chirality
Chirality () is a property of asymmetry important in several branches of science. The word ''chirality'' is derived from the Greek (''kheir''), "hand", a familiar chiral object.
An object or a system is ''chiral'' if it is distinguishable fro ...
of the whole 4-polytope just the way your bathroom mirror reverses the chirality of your image by a 180 degree reflection. Each 360 degree isoclinic rotation is as if the 24-cell surface had been stripped off like a glove and turned inside out, making a right-hand glove into a left-hand glove (or vice versa).
In a simple rotation of the 24-cell in a hexagonal plane, each vertex in the plane rotates first along an edge to an adjacent vertex 60 degrees away. But in an isoclinic rotation in ''two'' completely orthogonal planes one of which is a great hexagon, each vertex rotates first to a vertex ''two'' edge lengths away ( and 120° distant). The double 60-degree rotation's helical geodesics pass through every other vertex, missing the vertices in between. Each chord of the helical geodesic crosses between two Clifford parallel hexagon central planes, and lies in another hexagon central plane that intersects them both. The chords meet at a 60° angle, but since they lie in different planes they form a
helix
A helix (; ) is a shape like a cylindrical coil spring or the thread of a machine screw. It is a type of smooth space curve with tangent lines at a constant angle to a fixed axis. Helices are important in biology, as the DNA molecule is for ...
not a
triangle
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called ''vertices'', are zero-dimensional points while the sides connecting them, also called ''edges'', are one-dimension ...
. Three chords and 360° of rotation takes the vertex to an adjacent vertex, not back to itself. The helix of chords closes into a loop only after six chords: a 720° rotation twice around the 24-cell on a
skew hexagram
, can be seen as a compound polygon, compound composed of an upwards (blue here) and downwards (pink) facing equilateral triangle, with their intersection as a regular hexagon (in green).
A hexagram (Greek language, Greek) or sexagram (Latin l ...
with edges. Even though all 24 vertices and all the hexagons rotate at once, a 360 degree isoclinic rotation moves each vertex only halfway around its circuit. After 360 degrees each helix has departed from 3 vertices and reached a fourth vertex adjacent to the original vertex, but has ''not'' arrived back exactly at the vertex it departed from. Each central plane (every hexagon or square in the 24-cell) has rotated 360 degrees ''and'' been tilted sideways all the way around 360 degrees back to its original position (like a coin flipping twice), but the 24-cell's
orientation
Orientation may refer to:
Positioning in physical space
* Map orientation, the relationship between directions on a map and compass directions
* Orientation (housing), the position of a building with respect to the sun, a concept in building des ...
in the 4-space in which it is embedded is now different. Because the 24-cell is now inside-out, if the isoclinic rotation is continued in the ''same'' direction through another 360 degrees, the 24 moving vertices will pass through the other half of the vertices that were missed on the first revolution (the 12 antipodal vertices of the 12 that were hit the first time around), and each isoclinic geodesic ''will'' arrive back at the vertex it departed from, forming a closed six-chord helical loop. It takes a 720 degree isoclinic rotation for each
hexagram2 geodesic to complete a circuit through every ''second'' vertex of its six vertices by
winding around the 24-cell twice, returning the 24-cell to its original chiral orientation.
The hexagonal winding path that each vertex takes as it loops twice around the 24-cell forms a double helix bent into a
Möbius ring, so that the two strands of the double helix form a continuous single strand in a closed loop. In the first revolution the vertex traverses one 3-chord strand of the double helix; in the second revolution it traverses the second 3-chord strand, moving in the same rotational direction with the same handedness (bending either left or right) throughout. Although this isoclinic Möbius
ring
(The) Ring(s) may refer to:
* Ring (jewellery), a round band, usually made of metal, worn as ornamental jewelry
* To make a sound with a bell, and the sound made by a bell
Arts, entertainment, and media Film and TV
* ''The Ring'' (franchise), a ...
is a circular spiral through all 4 dimensions, not a 2-dimensional circle, like a great circle it is a geodesic because it is the shortest path from vertex to vertex.
Clifford parallel polytopes
Two planes are also called ''isoclinic'' if an isoclinic rotation will bring them together. The isoclinic planes are precisely those central planes with Clifford parallel geodesic great circles. Clifford parallel great circles do not intersect, so isoclinic great circle polygons have disjoint vertices. In the 24-cell every hexagonal central plane is isoclinic to three others, and every square central plane is isoclinic to five others. We can pick out 4 mutually isoclinic (Clifford parallel) great hexagons (four different ways) covering all 24 vertices of the 24-cell just once (a hexagonal fibration). We can pick out 6 mutually isoclinic (Clifford parallel) great squares (three different ways) covering all 24 vertices of the 24-cell just once (a square fibration). Every isoclinic rotation taking vertices to vertices corresponds to a discrete fibration.
Two dimensional great circle polygons are not the only polytopes in the 24-cell which are parallel in the Clifford sense. Congruent polytopes of 2, 3 or 4 dimensions can be said to be Clifford parallel in 4 dimensions if their corresponding vertices are all the same distance apart. The three 16-cells inscribed in the 24-cell are Clifford parallels. Clifford parallel polytopes are ''completely disjoint'' polytopes. A 60 degree isoclinic rotation in hexagonal planes takes each 16-cell to a disjoint 16-cell. Like all
double rotations, isoclinic rotations come in two
chiral
Chirality () is a property of asymmetry important in several branches of science. The word ''chirality'' is derived from the Greek language, Greek (''kheir''), "hand", a familiar chiral object.
An object or a system is ''chiral'' if it is dist ...
forms: there is a disjoint 16-cell to the ''left'' of each 16-cell, and another to its ''right''.
All Clifford parallel 4-polytopes are related by an isoclinic rotation, but not all isoclinic polytopes are Clifford parallels (completely disjoint). The three 8-cells in the 24-cell are isoclinic but not Clifford parallel. Like the 16-cells, they are rotated 60 degrees isoclinically with respect to each other, but their vertices are not all disjoint (and therefore not all equidistant). Each vertex occurs in two of the three 8-cells (as each 16-cell occurs in two of the three 8-cells).
Isoclinic rotations relate the convex regular 4-polytopes to each other. An isoclinic rotation of a single 16-cell will generate a 24-cell. A simple rotation of a single 16-cell will not, because its vertices will not reach either of the other two 16-cells' vertices in the course of the rotation. An isoclinic rotation of the 24-cell will generate the 600-cell, and an isoclinic rotation of the 600-cell will generate the 120-cell. (Or they can all be generated directly by an isoclinic rotation of the 16-cell, generating isoclinic copies of itself.) The different convex regular 4-polytopes nest inside each other, and multiple instances of the same 4-polytope hide next to each other in the Clifford parallel spaces that comprise the 3-sphere. For an object of more than one dimension, the only way to reach these parallel subspaces directly is by isoclinic rotation.
Rings
In the 24-cell there are sets of rings of six different kinds, described separately in detail in other sections of this article. This section describes how the different kinds of rings are
intertwined.
The 24-cell contains four kinds of
geodesic fibers (polygonal rings running through vertices):
great circle squares and their
isoclinic helix octagrams, and
great circle hexagons and their
isoclinic helix hexagrams. It also contains two kinds of
cell rings (chains of octahedra bent into a ring in the fourth dimension): four octahedra connected vertex-to-vertex and bent into a square, and six octahedra connected face-to-face and bent into a hexagon.
4-cell rings
Four unit-edge-length octahedra can be connected vertex-to-vertex along a common axis of length 4. The axis can then be bent into a square of edge length . Although it is possible to do this in a space of only three dimensions, that is not how it occurs in the 24-cell. Although the axes of the four octahedra occupy the same plane, forming one of the 18 great squares of the 24-cell, each octahedron occupies a different 3-dimensional hyperplane, and all four dimensions are utilized. The 24-cell can be partitioned into 6 such 4-cell rings (three different ways), mutually interlinked like adjacent links in a chain (but these
links all have a common center). An
isoclinic rotation in the great square plane by a multiple of 90° takes each octahedron in the ring to an octahedron in the ring.
6-cell rings

Six regular octahedra can be connected face-to-face along a common axis that passes through their centers of volume, forming a stack or column with only triangular faces. In a space of four dimensions, the axis can then be bent 60° in the fourth dimension at each of the six octahedron centers, in a plane orthogonal to all three orthogonal central planes of each octahedron, such that the top and bottom triangular faces of the column become coincident. The column becomes a ring around a hexagonal axis. The 24-cell can be partitioned into 4 such rings (four different ways), mutually interlinked. Because the hexagonal axis joins cell centers (not vertices), it is not a great hexagon of the 24-cell. However, six great hexagons can be found in the ring of six octahedra, running along the edges of the octahedra. In the column of six octahedra (before it is bent into a ring) there are six spiral paths along edges running up the column: three parallel helices spiraling clockwise, and three parallel helices spiraling counterclockwise. Each clockwise helix intersects each counterclockwise helix at two vertices three edge lengths apart. Bending the column into a ring changes these helices into great circle hexagons. The ring has two sets of three great hexagons, each on three Clifford parallel great circles. The great hexagons in each parallel set of three do not intersect, but each intersects the other three great hexagons (to which it is not Clifford parallel) at two antipodal vertices.
A
simple rotation in any of the great hexagon planes by a multiple of 60° rotates only that hexagon invariantly, taking each vertex in that hexagon to a vertex in the same hexagon. An
isoclinic rotation by 60° in any of the six great hexagon planes rotates all three Clifford parallel great hexagons invariantly, and takes each octahedron in the ring to a ''non-adjacent'' octahedron in the ring.
Each isoclinically displaced octahedron is also rotated itself. After a 360° isoclinic rotation each octahedron is back in the same position, but in a different orientation. In a 720° isoclinic rotation, its vertices are returned to their original
orientation
Orientation may refer to:
Positioning in physical space
* Map orientation, the relationship between directions on a map and compass directions
* Orientation (housing), the position of a building with respect to the sun, a concept in building des ...
.
Four Clifford parallel great hexagons comprise a discrete fiber bundle covering all 24 vertices in a
Hopf fibration. The 24-cell has four such
discrete hexagonal fibrations . Each great hexagon belongs to just one fibration, and the four fibrations are defined by disjoint sets of four great hexagons each. Each fibration is the domain (container) of a unique left-right pair of isoclinic rotations (left and right Hopf fiber bundles).
Four cell-disjoint 6-cell rings also comprise each discrete fibration defined by four Clifford parallel great hexagons. Each 6-cell ring contains only 18 of the 24 vertices, and only 6 of the 16 great hexagons, which we see illustrated above running along the cell ring's edges: 3 spiraling clockwise and 3 counterclockwise. Those 6 hexagons running along the cell ring's edges are not among the set of four parallel hexagons which define the fibration. For example, one of the four 6-cell rings in fibration
contains 3 parallel hexagons running clockwise along the cell ring's edges from fibration
, and 3 parallel hexagons running counterclockwise along the cell ring's edges from fibration
, but that cell ring contains no great hexagons from fibration
or fibration
.
The 24-cell contains 16 great hexagons, divided into four disjoint sets of four hexagons, each disjoint set uniquely defining a fibration. Each fibration is also a distinct set of four cell-disjoint 6-cell rings. The 24-cell has exactly 16 distinct 6-cell rings. Each 6-cell ring belongs to just one of the four fibrations.
Helical hexagrams and their isoclines
Another kind of geodesic fiber, the
helical hexagram isoclines, can be found within a 6-cell ring of octahedra. Each of these geodesics runs through every ''second'' vertex of a skew
hexagram
, can be seen as a compound polygon, compound composed of an upwards (blue here) and downwards (pink) facing equilateral triangle, with their intersection as a regular hexagon (in green).
A hexagram (Greek language, Greek) or sexagram (Latin l ...
2, which in the unit-radius, unit-edge-length 24-cell has six edges. The hexagram does not lie in a single central plane, but is composed of six linked chords from the six different hexagon great circles in the 6-cell ring. The isocline geodesic fiber is the path of an isoclinic rotation, a helical rather than simply circular path around the 24-cell which links vertices two edge lengths apart and consequently must wrap twice around the 24-cell before completing its six-vertex loop. Rather than a flat hexagon, it forms a
skew hexagram out of two three-sided 360 degree half-loops: open triangles joined end-to-end to each other in a six-sided Möbius loop.
Each 6-cell ring contains six such hexagram isoclines, three black and three white, that connect even and odd vertices respectively. Each of the three black-white pairs of isoclines belongs to one of the three fibrations in which the 6-cell ring occurs. Each fibration's right (or left) rotation traverses two black isoclines and two white isoclines in parallel, rotating all 24 vertices.
Beginning at any vertex at one end of the column of six octahedra, we can follow an isoclinic path of chords of an isocline from octahedron to octahedron. In the 24-cell the edges are
great hexagon edges (and octahedron edges); in the column of six octahedra we see six great hexagons running along the octahedra's edges. The chords are great hexagon diagonals, joining great hexagon vertices two edges apart. We find them in the ring of six octahedra running from a vertex in one octahedron to a vertex in the next octahedron, passing through the face shared by the two octahedra (but not touching any of the face's 3 vertices). Each chord is a chord of just one great hexagon (an edge of a
great triangle inscribed in that great hexagon), but successive chords belong to different great hexagons. At each vertex the isoclinic path of chords bends 60 degrees in two central planes at once: 60 degrees around the great hexagon that the chord before the vertex belongs to, and 60 degrees into the plane of a different great hexagon entirely, that the chord after the vertex belongs to. Thus the path follows one great hexagon from each octahedron to the next, but switches to another of the six great hexagons in the next link of the hexagram
2 path. Followed along the column of six octahedra (and "around the end" where the column is bent into a ring) the path may at first appear to be zig-zagging between three adjacent parallel hexagonal central planes (like a
Petrie polygon
In geometry, a Petrie polygon for a regular polytope of dimensions is a skew polygon in which every consecutive sides (but no ) belongs to one of the facets. The Petrie polygon of a regular polygon is the regular polygon itself; that of a reg ...
), but it is not: any isoclinic path we can pick out always zig-zags between ''two sets'' of three adjacent parallel hexagonal central planes, intersecting only every even (or odd) vertex and never changing its inherent even/odd parity, as it visits all six of the great hexagons in the 6-cell ring in rotation. When it has traversed one chord from each of the six great hexagons, after 720 degrees of isoclinic rotation (either left or right), it closes its skew hexagram and begins to repeat itself, circling again through the black (or white) vertices and cells.
At each vertex, there are four great hexagons and four hexagram isoclines (all black or all white) that cross at the vertex. Four hexagram isoclines (two black and two white) comprise a unique (left or right) fiber bundle of isoclines covering all 24 vertices in each distinct (left or right) isoclinic rotation. Each fibration has a unique left and right isoclinic rotation, and corresponding unique left and right fiber bundles of isoclines. There are 16 distinct hexagram isoclines in the 24-cell (8 black and 8 white). Each isocline is a skew ''Clifford polygon'' of no inherent chirality, but acts as a left (or right) isocline when traversed by a left (or right) rotation in different fibrations.
Helical octagrams and their isoclines
The 24-cell contains 18 helical
octagram
In geometry, an octagram is an eight-angled star polygon.
The name ''octagram'' combine a Greek numeral prefix, ''wikt:octa-, octa-'', with the Greek language, Greek suffix ''wikt:-gram, -gram''. The ''-gram'' suffix derives from γραμμή ...
isoclines (9 black and 9 white). Three pairs of octagram edge-helices are found in each of the three inscribed 16-cells, described elsewhere as the
helical construction of the 16-cell. In summary, each 16-cell can be decomposed (three different ways) into a left-right pair of 8-cell rings of -edged tetrahedral cells. Each 8-cell ring twists either left or right around an axial octagram helix of eight chords. In each 16-cell there are exactly 6 distinct helices, identical octagrams which each circle through all eight vertices. Each acts as either a left helix or a right helix or a Petrie polygon in each of the six distinct isoclinic rotations (three left and three right), and has no inherent chirality except in respect to a particular rotation. Adjacent vertices on the octagram isoclines are = 90° apart, so the circumference of the isocline is 4𝝅. An ''isoclinic'' rotation by 90° in great square invariant planes takes each vertex to its antipodal vertex, four vertices away in either direction along the isocline, and = 180° distant across the diameter of the isocline.
Each of the 3 fibrations of the 24-cell's 18 great squares corresponds to a distinct left (and right) isoclinic rotation in great square invariant planes. Each 60° step of the rotation takes 6 disjoint great squares (2 from each 16-cell) to great squares in a neighboring 16-cell, on
8-chord helical isoclines characteristic of the 16-cell.
In the 24-cell, these 18 helical octagram isoclines can be found within the six orthogonal
4-cell rings of octahedra. Each 4-cell ring has cells bonded vertex-to-vertex around a great square axis, and we find antipodal vertices at opposite vertices of the great square. A chord (the diameter of the great square and of the isocline) connects them.
Boundary cells describes how the axes of the 24-cell's octahedral cells are the edges of the 16-cell's tetrahedral cells, each tetrahedron is inscribed in a (tesseract) cube, and each octahedron is inscribed in a pair of cubes (from different tesseracts), bridging them. The vertex-bonded octahedra of the 4-cell ring also lie in different tesseracts. The isocline's four diameter chords form an
octagram8=4 with edges that each run from the vertex of one cube and octahedron and tetrahedron, to the vertex of another cube and octahedron and tetrahedron (in a different tesseract), straight through the center of the 24-cell on one of the 12 axes.
The octahedra in the 4-cell rings are vertex-bonded to more than two other octahedra, because three 4-cell rings (and their three axial great squares, which belong to different 16-cells) cross at 90° at each bonding vertex. At that vertex the octagram makes two right-angled turns at once: 90° around the great square, and 90° orthogonally into a different 4-cell ring entirely. The 180° four-edge arc joining two ends of each diameter chord of the octagram runs through the volumes and opposite vertices of two face-bonded tetrahedra (in the same 16-cell), which are also the opposite vertices of two vertex-bonded octahedra in different 4-cell rings (and different tesseracts). The
720° octagram isocline runs through 8 vertices of the four-cell ring and through the volumes of 16 tetrahedra. At each vertex, there are three great squares and six octagram isoclines (three black-white pairs) that cross at the vertex.
This is the characteristic rotation of the 16-cell, ''not'' the 24-cell's characteristic rotation, and it does not take whole 16-cells ''of the 24-cell'' to each other the way the
24-cell's rotation in great hexagon planes does.
Characteristic orthoscheme
Every regular 4-polytope has its
characteristic 4-orthoscheme, an
irregular 5-cell. The characteristic 5-cell of the regular 24-cell is represented by the
Coxeter-Dynkin diagram , which can be read as a list of the dihedral angles between its mirror facets. It is an irregular
tetrahedral pyramid based on the
characteristic tetrahedron of the regular octahedron. The regular 24-cell is subdivided by its symmetry hyperplanes into 1152 instances of its characteristic 5-cell that all meet at its center.
The characteristic 5-cell (4-orthoscheme) has four more edges than its base characteristic tetrahedron (3-orthoscheme), joining the four vertices of the base to its apex (the fifth vertex of the 4-orthoscheme, at the center of the regular 24-cell). If the regular 24-cell has radius and edge length 𝒍 = 1, its characteristic 5-cell's ten edges have lengths
,
,
around its exterior right-triangle face (the edges opposite the ''characteristic angles'' 𝟀, 𝝉, 𝟁), plus
,
,
(the other three edges of the exterior 3-orthoscheme facet the characteristic tetrahedron, which are the ''characteristic radii'' of the octahedron), plus
,
,
,
(edges which are the characteristic radii of the 24-cell). The 4-edge path along orthogonal edges of the orthoscheme is
,
,
,
, first from a 24-cell vertex to a 24-cell edge center, then turning 90° to a 24-cell face center, then turning 90° to a 24-cell octahedral cell center, then turning 90° to the 24-cell center.
Reflections
The 24-cell can be
constructed by the reflections of its characteristic 5-cell in its own facets (its tetrahedral mirror walls). Reflections and rotations are related: a reflection in an ''even'' number of ''intersecting'' mirrors is a rotation. Consequently, regular polytopes can be generated by reflections or by rotations. For example, any
720° isoclinic rotation of the 24-cell in a hexagonal invariant plane takes ''each'' of the 24 vertices to and through 5 other vertices and back to itself, on a skew
hexagram2 geodesic isocline that winds twice around the 3-sphere on every ''second'' vertex of the hexagram. Any set of
four orthogonal pairs of antipodal vertices (the 8 vertices of one of the
three inscribed 16-cells) performing ''half'' such an orbit visits 3 * 8 = 24 distinct vertices and
generates the 24-cell sequentially in 3 steps of a single 360° isoclinic rotation, just as any single characteristic 5-cell reflecting itself in its own mirror walls generates the 24 vertices simultaneously by reflection.
Tracing the orbit of ''one'' such 16-cell vertex during the 360° isoclinic rotation reveals more about the relationship between reflections and rotations as generative operations. The vertex follows an
isocline (a doubly curved geodesic circle) rather than an ordinary great circle. The isocline connects vertices two edge lengths apart, but curves away from the great circle path over the two edges connecting those vertices, missing the vertex in between. Although the isocline does not follow any one great circle, it is contained within a ring of another kind: in the 24-cell it stays within a
6-cell ring of spherical octahedral cells, intersecting one vertex in each cell, and passing through the volume of two adjacent cells near the missed vertex.
Chiral symmetry operations
A
symmetry operation
In mathematics, a symmetry operation is a geometric transformation of an object that leaves the object looking the same after it has been carried out. For example, a turn rotation of a regular triangle about its center (geometry), center, a refle ...
is a rotation or reflection which leaves the object indistinguishable from itself before the transformation. The 24-cell has 1152 distinct symmetry operations (576 rotations and 576 reflections). Each rotation is equivalent to two
reflections, in a distinct pair of non-parallel mirror planes.
Pictured are sets of disjoint
great circle polygons, each in a distinct central plane of the 24-cell. For example, =4 is an orthogonal projection of the 24-cell picturing 4 of its
6great hexagon planes. The 4 planes lie Clifford parallel to the projection plane and to each other, and their great polygons collectively constitute a discrete
Hopf fibration of 4 non-intersecting great circles which visit all 24 vertices just once.
Each row of the table describes a class of distinct rotations. Each rotation class takes the left planes pictured to the corresponding right planes pictured. The vertices of the moving planes move in parallel along the polygonal isocline paths pictured. For example, the
rotation class consists of
2distinct rotational displacements by an arc-distance of = 120° between 16 great hexagon planes represented by quaternion group
and a corresponding set of 16 great hexagon planes represented by quaternion group
. One of the
2distinct rotations of this class moves the representative
vertex coordinate to the vertex coordinate
.
}, name=lines of symmetry
, rowspan=2,
=6 82𝝅
, colspan=4,
, - style="background: white;",
, 2𝝅
, 360°
,
, 0
,
, 90°
,
, 1.414~
,
, 90°
,
, 1.414~
, - style="background: white;",
, rowspan=2,
=12 84𝝅
, colspan=4,
, rowspan=2,
=6 82𝝅
, colspan=4,
, rowspan=2,
=6 82𝝅
, colspan=4,
, - style="background: white;",
, 𝝅
, 180°
,
, 2
,
, 90°
,
, 1.414~
,
, 90°
,
, 1.414~
, - style="background: white;",
, rowspan=2,
=3 24𝝅
, colspan=4,
, rowspan=2,
=6 22𝝅
, colspan=4,
, rowspan=2,
=6 22𝝅
, colspan=4,
, - style="background: white;",
,
, 90°
,
, 1.414~
,
, 90°
,
, 1.414~
, 𝝅
, 180°
,
, 2
, - style="background: white;",
, rowspan=2,
= 6
64𝝅
, colspan=4,
, rowspan=2,
=6 62𝝅
, colspan=4,
, rowspan=2,
=6 62𝝅
, colspan=4,
, - style="background: white;",
, 2𝝅
, 360°
,
, 0
,
, 90°
,
, 1.414~
,
, 90°
,
, 1.414~
, - style="background: #E6FFEE;",
, rowspan=2,
=2 84𝝅
, colspan=4,
, rowspan=2,
=6 82𝝅
, colspan=4,
, rowspan=2,
=4 82𝝅
, colspan=4,
, - style="background: #E6FFEE;",
,
, 60°
,
, 1
,
, 90°
,
, 1.414~
,
, 60°
,
, 1
, - style="background: white;",
, rowspan=2,
=12 4𝝅
, colspan=4,
, rowspan=2,
=6 2𝝅
, colspan=4,
, rowspan=2,
=6 2𝝅
, colspan=4,
, - style="background: white;",
, 𝝅
, 180°
,
, 2
,
, 90°
,
, 1.414~
,
, 90°
,
, 1.414~
, - style="background: white;",
, rowspan=2,
=12 24𝝅
, colspan=4,
, rowspan=2,
=12 22𝝅
, colspan=4,
, rowspan=2,
=12 22𝝅
, colspan=4,
, - style="background: white;",
,
, 90°
,
, 1.414~
,
, 90°
,
, 1.414~
,
, 90°
,
, 1.414~
, - style="background: white;",
, rowspan=2,
=
0𝝅
, colspan=4,
, rowspan=2,
=12 2𝝅
, colspan=4,
, rowspan=2,
=12 2𝝅
, colspan=4,
, - style="background: white;",
, 0
, 0°
,
, 0
,
, 90°
,
, 1.414~
,
, 90°
,
, 1.414~
, - style="background: white;",
, rowspan=2,
=12 22𝝅
, colspan=4,
, rowspan=2,
=12 22𝝅
, colspan=4,
, rowspan=2,
=12 22𝝅
, colspan=4,
, - style="background: white;",
, 𝝅
, 180°
,
, 2
,
, 90°
,
, 1.414~
,
, 90°
,
, 1.414~
In a rotation class
 In
In  The 24 vertices of the 24-cell are distributed at four different chord lengths from each other: , , and . The chords (the 24-cell edges) are the edges of central hexagons, and the chords are the diagonals of central hexagons. The chords are the edges of central squares, and the chords are the diagonals of central squares.
Each vertex is joined to 8 others by an edge of length 1, spanning 60° = of arc. Next nearest are 6 vertices located 90° = away, along an interior chord of length . Another 8 vertices lie 120° = away, along an interior chord of length . The opposite vertex is 180° = away along a diameter of length 2. Finally, as the 24-cell is radially equilateral, its center is 1 edge length away from all vertices.
To visualize how the interior polytopes of the 24-cell fit together (as described
The 24 vertices of the 24-cell are distributed at four different chord lengths from each other: , , and . The chords (the 24-cell edges) are the edges of central hexagons, and the chords are the diagonals of central hexagons. The chords are the edges of central squares, and the chords are the diagonals of central squares.
Each vertex is joined to 8 others by an edge of length 1, spanning 60° = of arc. Next nearest are 6 vertices located 90° = away, along an interior chord of length . Another 8 vertices lie 120° = away, along an interior chord of length . The opposite vertex is 180° = away along a diameter of length 2. Finally, as the 24-cell is radially equilateral, its center is 1 edge length away from all vertices.
To visualize how the interior polytopes of the 24-cell fit together (as described  When interpreted as the
When interpreted as the  The regular convex 4-polytopes are an expression of their underlying
The regular convex 4-polytopes are an expression of their underlying  Six regular octahedra can be connected face-to-face along a common axis that passes through their centers of volume, forming a stack or column with only triangular faces. In a space of four dimensions, the axis can then be bent 60° in the fourth dimension at each of the six octahedron centers, in a plane orthogonal to all three orthogonal central planes of each octahedron, such that the top and bottom triangular faces of the column become coincident. The column becomes a ring around a hexagonal axis. The 24-cell can be partitioned into 4 such rings (four different ways), mutually interlinked. Because the hexagonal axis joins cell centers (not vertices), it is not a great hexagon of the 24-cell. However, six great hexagons can be found in the ring of six octahedra, running along the edges of the octahedra. In the column of six octahedra (before it is bent into a ring) there are six spiral paths along edges running up the column: three parallel helices spiraling clockwise, and three parallel helices spiraling counterclockwise. Each clockwise helix intersects each counterclockwise helix at two vertices three edge lengths apart. Bending the column into a ring changes these helices into great circle hexagons. The ring has two sets of three great hexagons, each on three Clifford parallel great circles. The great hexagons in each parallel set of three do not intersect, but each intersects the other three great hexagons (to which it is not Clifford parallel) at two antipodal vertices.
A simple rotation in any of the great hexagon planes by a multiple of 60° rotates only that hexagon invariantly, taking each vertex in that hexagon to a vertex in the same hexagon. An isoclinic rotation by 60° in any of the six great hexagon planes rotates all three Clifford parallel great hexagons invariantly, and takes each octahedron in the ring to a ''non-adjacent'' octahedron in the ring.
Each isoclinically displaced octahedron is also rotated itself. After a 360° isoclinic rotation each octahedron is back in the same position, but in a different orientation. In a 720° isoclinic rotation, its vertices are returned to their original
Six regular octahedra can be connected face-to-face along a common axis that passes through their centers of volume, forming a stack or column with only triangular faces. In a space of four dimensions, the axis can then be bent 60° in the fourth dimension at each of the six octahedron centers, in a plane orthogonal to all three orthogonal central planes of each octahedron, such that the top and bottom triangular faces of the column become coincident. The column becomes a ring around a hexagonal axis. The 24-cell can be partitioned into 4 such rings (four different ways), mutually interlinked. Because the hexagonal axis joins cell centers (not vertices), it is not a great hexagon of the 24-cell. However, six great hexagons can be found in the ring of six octahedra, running along the edges of the octahedra. In the column of six octahedra (before it is bent into a ring) there are six spiral paths along edges running up the column: three parallel helices spiraling clockwise, and three parallel helices spiraling counterclockwise. Each clockwise helix intersects each counterclockwise helix at two vertices three edge lengths apart. Bending the column into a ring changes these helices into great circle hexagons. The ring has two sets of three great hexagons, each on three Clifford parallel great circles. The great hexagons in each parallel set of three do not intersect, but each intersects the other three great hexagons (to which it is not Clifford parallel) at two antipodal vertices.
A simple rotation in any of the great hexagon planes by a multiple of 60° rotates only that hexagon invariantly, taking each vertex in that hexagon to a vertex in the same hexagon. An isoclinic rotation by 60° in any of the six great hexagon planes rotates all three Clifford parallel great hexagons invariantly, and takes each octahedron in the ring to a ''non-adjacent'' octahedron in the ring.
Each isoclinically displaced octahedron is also rotated itself. After a 360° isoclinic rotation each octahedron is back in the same position, but in a different orientation. In a 720° isoclinic rotation, its vertices are returned to their original