Étendue on:
[Wikipedia]
[Google]
[Amazon]
Etendue or Ă©tendue (; ) is a property of
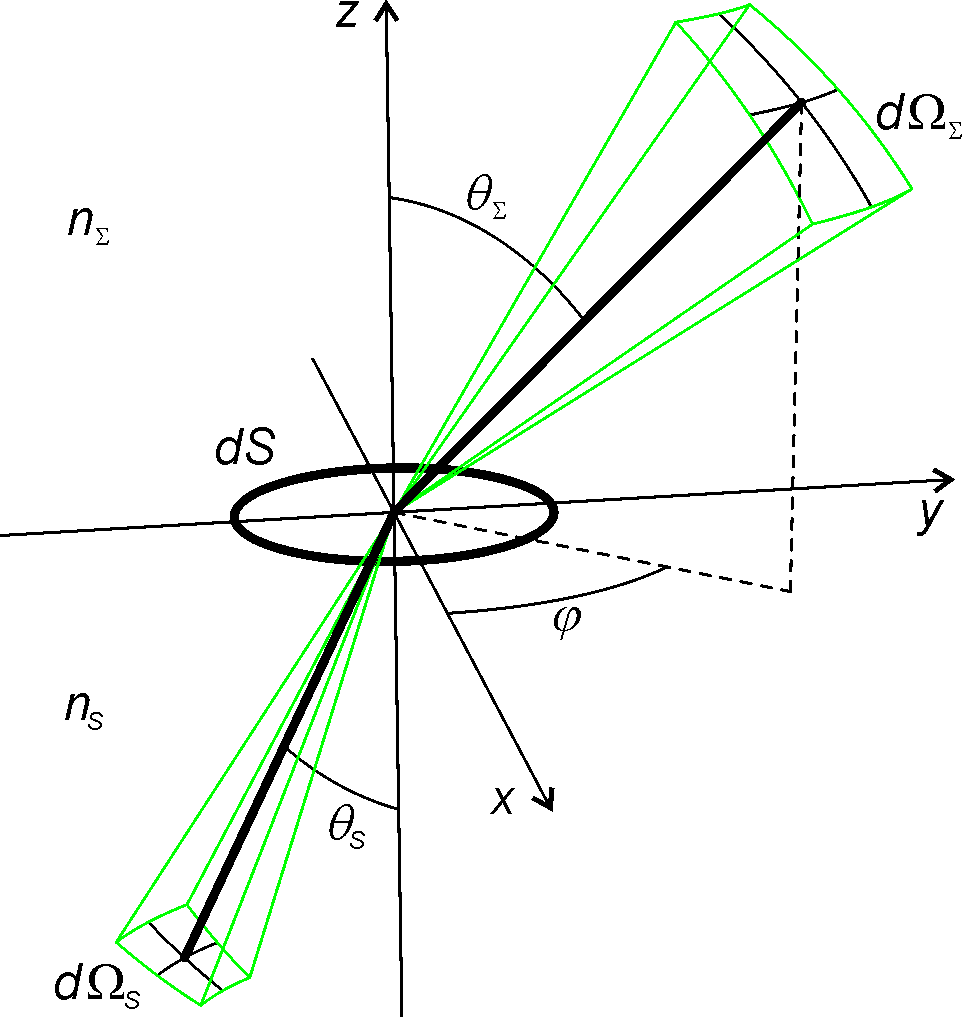
 An infinitesimal surface element, , with normal is immersed in a medium of
An infinitesimal surface element, , with normal is immersed in a medium of
 The conservation of etendue discussed above applies to the case of light propagation in free space, or more generally, in a medium of any
The conservation of etendue discussed above applies to the case of light propagation in free space, or more generally, in a medium of any
 In the context of Hamiltonian optics, at a point in space, a light ray may be completely defined by a point , a unit
In the context of Hamiltonian optics, at a point in space, a light ray may be completely defined by a point , a unit
 Consider an infinitesimal surface , immersed in a medium of refractive index crossed by (or emitting) light inside a cone of angle . The etendue of this light is given by
Noting that is the
Consider an infinitesimal surface , immersed in a medium of refractive index crossed by (or emitting) light inside a cone of angle . The etendue of this light is given by
Noting that is the  The limit on maximum concentration (shown) is an optic with an entrance aperture , in air () collecting light within a solid angle of angle (its acceptance angle) and sending it to a smaller area receiver immersed in a medium of refractive index , whose points are illuminated within a solid angle of angle . From the above expression, the etendue of the incoming light is
and the etendue of the light reaching the receiver is
Conservation of etendue then gives
where is the concentration of the optic. For a given angular aperture , of the incoming light, this concentration will be maximum for the maximum value of , that is . The maximum possible concentration is then
In the case that the incident index is not unity, we have
and so
and in the best-case limit of , this becomes
If the optic were a collimator instead of a concentrator, the light direction is reversed and conservation of etendue gives us the minimum aperture, , for a given output full angle .
The limit on maximum concentration (shown) is an optic with an entrance aperture , in air () collecting light within a solid angle of angle (its acceptance angle) and sending it to a smaller area receiver immersed in a medium of refractive index , whose points are illuminated within a solid angle of angle . From the above expression, the etendue of the incoming light is
and the etendue of the light reaching the receiver is
Conservation of etendue then gives
where is the concentration of the optic. For a given angular aperture , of the incoming light, this concentration will be maximum for the maximum value of , that is . The maximum possible concentration is then
In the case that the incident index is not unity, we have
and so
and in the best-case limit of , this becomes
If the optic were a collimator instead of a concentrator, the light direction is reversed and conservation of etendue gives us the minimum aperture, , for a given output full angle .
light
Light, visible light, or visible radiation is electromagnetic radiation that can be visual perception, perceived by the human eye. Visible light spans the visible spectrum and is usually defined as having wavelengths in the range of 400– ...
in an optical system, which characterizes how "spread out" the light is in area and angle. It corresponds to the beam parameter product (BPP) in Gaussian beam
In optics, a Gaussian beam is an idealized beam of electromagnetic radiation whose amplitude envelope in the transverse plane is given by a Gaussian function; this also implies a Gaussian intensity (irradiance) profile. This fundamental (or ...
optics. Other names for etendue include acceptance, throughput, light grasp, light-gathering power, optical extent, and the AΩ product. ''Throughput'' and ''AΩ product'' are especially used in radiometry
Radiometry is a set of techniques for measurement, measuring electromagnetic radiation, including visible light. Radiometric techniques in optics characterize the distribution of the radiation's power (physics), power in space, as opposed to phot ...
and radiative transfer where it is related to the view factor (or shape factor). It is a central concept in nonimaging optics.
From the source point of view, etendue is the product of the area of the source and the solid angle that the system's entrance pupil subtends as seen from the source. Equivalently, from the system point of view, the etendue equals the area of the entrance pupil times the solid angle the source subtends as seen from the pupil. These definitions must be applied for infinitesimally small "elements" of area and solid angle, which must then be summed over both the source and the diaphragm as shown below. Etendue may be considered to be a volume in phase space
The phase space of a physical system is the set of all possible physical states of the system when described by a given parameterization. Each possible state corresponds uniquely to a point in the phase space. For mechanical systems, the p ...
.
Etendue never decreases in any optical system where optical power is conserved. A perfect optical system produces an image with the same etendue as the source. The etendue is related to the Lagrange invariant and the optical invariant, which also share the property of being constant in an ideal optical system. The radiance of an optical system is equal to the derivative of the radiant flux
In radiometry, radiant flux or radiant power is the radiant energy emitted, reflected, transmitted, or received per unit time, and spectral flux or spectral power is the radiant flux per unit frequency or wavelength, depending on whether the ...
with respect to the etendue.
Definition
 An infinitesimal surface element, , with normal is immersed in a medium of
An infinitesimal surface element, , with normal is immersed in a medium of refractive index
In optics, the refractive index (or refraction index) of an optical medium is the ratio of the apparent speed of light in the air or vacuum to the speed in the medium. The refractive index determines how much the path of light is bent, or refrac ...
. The surface is crossed by (or emits) light confined to a solid angle, , at an angle with the normal . The area of projected in the direction of the light propagation is . The etendue of an infinitesimal bundle of light crossing is defined as
Etendue is the product of geometric extent and the squared refractive index of a medium through which the beam propagates. Because angles, solid angles, and refractive indices are dimensionless quantities, etendue is often expressed in units of area (given by ). However, it can alternatively be expressed in units of area (square meters) multiplied by solid angle (steradians).
In free space
Consider a light source , and a light detector , both of which are extended surfaces (rather than differential elements), and which are separated by a medium of refractive index that is perfectly transparent (shown). To compute the etendue of the system, one must consider the contribution of each point on the surface of the light source as they cast rays to each point on the receiver. According to the definition above, the etendue of the light crossing towards is given by: where is the solid angle defined by area at area , and is the distance between the two areas. Similarly, the etendue of the light crossing coming from is given by: where is the solid angle defined by area . These expressions result in showing that etendue is conserved as light propagates in free space. The etendue of the whole system is then: If both surfaces and are immersed in air (or in vacuum), and the expression above for the etendue may be written as where is the view factor between differential surfaces and . Integration on and results in which allows the etendue between two surfaces to be obtained from the view factors between those surfaces.Conservation
The etendue of a given bundle of light is conserved: etendue can be increased, but not decreased in any optical system. This means that any system that concentrates light from some source onto a smaller area must always increase the solid angle of incidence (that is, the area of the sky that the source subtends). For example, a magnifying glass can increase the intensity of sunlight onto a small spot, but does so because, viewed from the spot that the light is concentrated onto, the apparent size of the sun is increased proportional to the concentration. As shown below, etendue is conserved as light travels through free space and at refractions or reflections. It is then also conserved as light travels through optical systems where it undergoes perfect reflections or refractions. However, if light was to hit, say, a diffuser, its solid angle would increase, increasing the etendue. Etendue can then remain constant or it can increase as light propagates through an optic, but it cannot decrease. This is a direct result of the fact thatentropy
Entropy is a scientific concept, most commonly associated with states of disorder, randomness, or uncertainty. The term and the concept are used in diverse fields, from classical thermodynamics, where it was first recognized, to the micros ...
must be constant or increasing.
Conservation of etendue can be derived in different contexts, such as from optical first principles, from Hamiltonian optics or from the second law of thermodynamics
The second law of thermodynamics is a physical law based on Universal (metaphysics), universal empirical observation concerning heat and Energy transformation, energy interconversions. A simple statement of the law is that heat always flows spont ...
.
From the perspective of thermodynamics, etendue is a form of entropy. Specifically, the etendue of a bundle of light contributes to the entropy of it by . Etendue may be exponentially decreased by an increase in entropy elsewhere. For example, a material might absorb photons and emit lower-frequency photons, and emit the difference in energy as heat. This increases entropy due to heat, allowing a corresponding decrease in etendue.
The conservation of etendue in free space is related to the reciprocity theorem for view factors.
In refractions and reflections
 The conservation of etendue discussed above applies to the case of light propagation in free space, or more generally, in a medium of any
The conservation of etendue discussed above applies to the case of light propagation in free space, or more generally, in a medium of any refractive index
In optics, the refractive index (or refraction index) of an optical medium is the ratio of the apparent speed of light in the air or vacuum to the speed in the medium. The refractive index determines how much the path of light is bent, or refrac ...
. In particular, etendue is conserved in refractions and reflections. Figure "etendue in refraction" shows an infinitesimal surface on the plane separating two media of refractive indices and .
The normal to points in the direction of the -axis. Incoming light is confined to a solid angle and reaches at an angle to its normal. Refracted light is confined to a solid angle and leaves at an angle to its normal. The directions of the incoming and refracted light are contained in a plane making an angle to the -axis, defining these directions in a spherical coordinate system
In mathematics, a spherical coordinate system specifies a given point in three-dimensional space by using a distance and two angles as its three coordinates. These are
* the radial distance along the line connecting the point to a fixed point ...
. With these definitions, Snell's law of refraction can be written as
and its derivative relative to
multiplied by each other result in
where both sides of the equation were also multiplied by which does not change on refraction. This expression can now be written as
Multiplying both sides by we get
that is
showing that the etendue of the light refracted at is conserved. The same result is also valid for the case of a reflection at a surface , in which case and .
Brightness theorem
A consequence of the conservation of etendue is the ''brightness theorem'', which states that no linear optical system can increase the brightness of the light emitted from a source to a higher value than the brightness of the surface of that source (where "brightness" is defined as the optical power emitted per unit solid angle per unit emitting or receiving area).Conservation of basic radiance
Radiance of a surface is related to etendue by: where * is theradiant flux
In radiometry, radiant flux or radiant power is the radiant energy emitted, reflected, transmitted, or received per unit time, and spectral flux or spectral power is the radiant flux per unit frequency or wavelength, depending on whether the ...
emitted, reflected, transmitted or received;
* is the refractive index in which that surface is immersed;
* is the Ă©tendue of the light beam.
As the light travels through an ideal optical system, both the etendue and the radiant flux are conserved. Therefore, ''basic radiance'' defined as:
is also conserved. In real systems, the etendue may increase (for example due to scattering) or the radiant flux may decrease (for example due to absorption) and, therefore, basic radiance may decrease. However, etendue may not decrease and radiant flux may not increase and, therefore, basic radiance may not increase.
As a volume in phase space
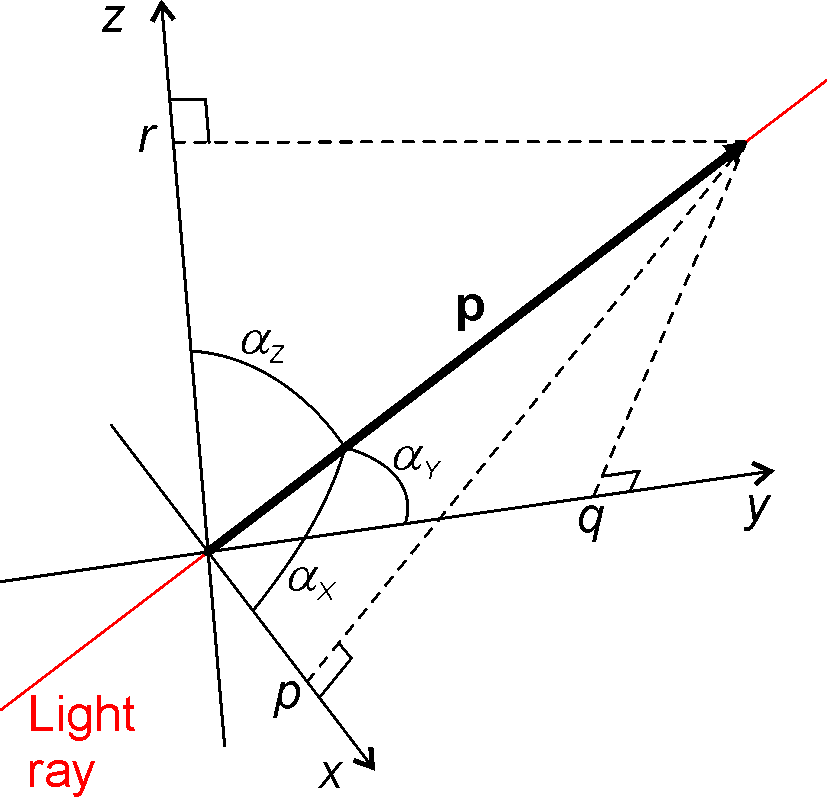
 In the context of Hamiltonian optics, at a point in space, a light ray may be completely defined by a point , a unit
In the context of Hamiltonian optics, at a point in space, a light ray may be completely defined by a point , a unit Euclidean vector
In mathematics, physics, and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector or spatial vector) is a geometric object that has magnitude (or length) and direction. Euclidean vectors can be added and scal ...
indicating its direction and the refractive index at point . The optical momentum of the ray at that point is defined by
where . The geometry of the optical momentum vector is illustrated in figure "optical momentum".
In a spherical coordinate system
In mathematics, a spherical coordinate system specifies a given point in three-dimensional space by using a distance and two angles as its three coordinates. These are
* the radial distance along the line connecting the point to a fixed point ...
may be written as
from which
and therefore, for an infinitesimal area on the -plane immersed in a medium of refractive index , the etendue is given by
which is an infinitesimal volume in phase space . Conservation of etendue in phase space is the equivalent in optics to Liouville's theorem in classical mechanics. Etendue as volume in phase space is commonly used in nonimaging optics.
Maximum concentration
 Consider an infinitesimal surface , immersed in a medium of refractive index crossed by (or emitting) light inside a cone of angle . The etendue of this light is given by
Noting that is the
Consider an infinitesimal surface , immersed in a medium of refractive index crossed by (or emitting) light inside a cone of angle . The etendue of this light is given by
Noting that is the numerical aperture
In optics, the numerical aperture (NA) of an optical system is a dimensionless number that characterizes the range of angles over which the system can accept or emit light. By incorporating index of refraction in its definition, has the property ...
''NA'', of the beam of light, this can also be expressed as
Note that is expressed in a spherical coordinate system
In mathematics, a spherical coordinate system specifies a given point in three-dimensional space by using a distance and two angles as its three coordinates. These are
* the radial distance along the line connecting the point to a fixed point ...
. Now, if a large surface is crossed by (or emits) light also confined to a cone of angle , the etendue of the light crossing is
 The limit on maximum concentration (shown) is an optic with an entrance aperture , in air () collecting light within a solid angle of angle (its acceptance angle) and sending it to a smaller area receiver immersed in a medium of refractive index , whose points are illuminated within a solid angle of angle . From the above expression, the etendue of the incoming light is
and the etendue of the light reaching the receiver is
Conservation of etendue then gives
where is the concentration of the optic. For a given angular aperture , of the incoming light, this concentration will be maximum for the maximum value of , that is . The maximum possible concentration is then
In the case that the incident index is not unity, we have
and so
and in the best-case limit of , this becomes
If the optic were a collimator instead of a concentrator, the light direction is reversed and conservation of etendue gives us the minimum aperture, , for a given output full angle .
The limit on maximum concentration (shown) is an optic with an entrance aperture , in air () collecting light within a solid angle of angle (its acceptance angle) and sending it to a smaller area receiver immersed in a medium of refractive index , whose points are illuminated within a solid angle of angle . From the above expression, the etendue of the incoming light is
and the etendue of the light reaching the receiver is
Conservation of etendue then gives
where is the concentration of the optic. For a given angular aperture , of the incoming light, this concentration will be maximum for the maximum value of , that is . The maximum possible concentration is then
In the case that the incident index is not unity, we have
and so
and in the best-case limit of , this becomes
If the optic were a collimator instead of a concentrator, the light direction is reversed and conservation of etendue gives us the minimum aperture, , for a given output full angle .
See also
* Beam emittance * Beam parameter product *Light field
A light field, or lightfield, is a vector-valued function, vector function that describes the amount of light flowing in every direction through every point in a space. The space of all possible ''light rays'' is given by the Five-dimensional space ...
*Noether's theorem
Noether's theorem states that every continuous symmetry of the action of a physical system with conservative forces has a corresponding conservation law. This is the first of two theorems (see Noether's second theorem) published by the mat ...
* Symplectic geometry
References
Further reading
* *xkcd
''xkcd'' is a serial webcomic created in 2005 by American author Randall Munroe. Sometimes styled ''XKCD'', the comic's tagline describes it as "a webcomic of romance, sarcasm, math, and language". Munroe states on the comic's website that the ...
–author Randall Munroe explains why it's impossible to light a fire with concentrated moonlight using an etendue-conservation argument.
* {{cite journal , last1= Sun , first1= Xutao , last2= Zheng , first2= Zhenrong , last3= Liu , first3= Xu , last4= Gu , first4= Peifu , date= March 2006 , title= Etendue Analysis and Measurement of Light Source with Elliptical Reflector , journal= Displays , volume= 27 , issue= 2 , pages= 56–61
Optical quantities