|
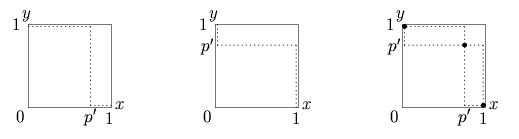
War Of Attrition (game)
In game theory, the war of attrition is a dynamic timing game in which players choose a time to stop, and fundamentally trade off the strategic gains from outlasting other players and the real costs expended with the passage of time. Its precise opposite is the ''pre-emption game'', in which players elect a time to stop, and fundamentally trade off the strategic costs from outlasting other players and the real gains occasioned by the passage of time. The model was originally formulated by John Maynard Smith; a mixed evolutionarily stable strategy (ESS) was determined by Bishop & Cannings. An example is a second price ''all-pay'' auction, in which the prize goes to the player with the highest bid and each player pays the loser's low bid (making it an all-pay sealed-bid second-price auction). Examining the game To see how a war of attrition works, consider the all pay auction: Assume that each player makes a bid on an item, and the one who bids the highest wins a resource of value ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Game Theory
Game theory is the study of mathematical models of strategic interactions. It has applications in many fields of social science, and is used extensively in economics, logic, systems science and computer science. Initially, game theory addressed two-person zero-sum games, in which a participant's gains or losses are exactly balanced by the losses and gains of the other participant. In the 1950s, it was extended to the study of non zero-sum games, and was eventually applied to a wide range of Human behavior, behavioral relations. It is now an umbrella term for the science of rational Decision-making, decision making in humans, animals, and computers. Modern game theory began with the idea of mixed-strategy equilibria in two-person zero-sum games and its proof by John von Neumann. Von Neumann's original proof used the Brouwer fixed-point theorem on continuous mappings into compact convex sets, which became a standard method in game theory and mathematical economics. His paper was f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Symmetric Equilibrium
In game theory, a symmetric equilibrium is an equilibrium where all players use the same strategy (possibly mixed) in the equilibrium. In the Prisoner's Dilemma game pictured to the right, the only Nash equilibrium is (''D'', ''D''). Since both players use the same strategy, the equilibrium is symmetric. Symmetric equilibria have important properties. Only symmetric equilibria can be evolutionarily stable states in single population models. See also *Symmetric game In game theory, a symmetric game is a game where the payoffs for playing a particular strategy depend only on the other strategies employed, not on who is playing them. If one can change the identities of the players without changing the payoff t ... References {{DEFAULTSORT:Symmetric Equilibrium Game theory equilibrium concepts ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dollar Auction
The dollar auction is a non-zero sum sequential game explored by economist Martin Shubik to illustrate how a short-sighted approach to rational choice can lead to decisions that are, in the long-run, irrational. Shubik: 1971. Page 109 Play The setup involves an auctioneer who volunteers to auction off a dollar bill with the following rule: the bill goes to the winner; however, the second-highest bidder also loses the amount that they bid, making them the biggest loser in the auction. The winner can get a dollar for a mere 5 cents (the minimum bid), but only if no one else enters into the bidding war. However, entering the auction with a low bid may result in a problematic outcome. For instance, a player might begin by bidding 5 cents, hoping to make a 95-cent profit. They can be outbid by another player bidding 10 cents, as a 90-cent profit is still desirable. Similarly, another bidder may bid 15 cents, making an 85-cent profit. Meanwhile, the second bidder may attempt to conve ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hawk-dove Game
The game of chicken, also known as the hawk-dove game or snowdrift game, is a model of conflict for two players in game theory. The principle of the game is that while the ideal outcome is for one player to yield (to avoid the worst outcome if neither yields), individuals try to avoid it out of pride, not wanting to look like "chickens". Each player taunts the other to increase the risk of shame in yielding. However, when one player yields, the conflict is avoided, and the game essentially ends. The name "chicken" has its origins in a game in which two drivers drive toward each other on a collision course: one must swerve, or both may die in the crash, but if one driver swerves and the other does not, the one who swerved will be called a "chicken", meaning a coward; this terminology is most prevalent in political science and economics. The name "hawk–dove" refers to a situation in which there is a competition for a shared resource and the contestants can choose either conciliat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rubinstein Bargaining Model
Rubinstein bargaining model refers to a class of bargaining games in game theory featuring alternating offers between two players over an infinite time horizon. The model addresses how rational agents divide a surplus when they have conflicting interests but mutual incentives to reach an agreement. The original solution concept was introduced by Ariel Rubinstein in his seminal 1982 paper. Prior to Rubinstein's work, cooperative game theory approaches like the Nash bargaining solution provided normative benchmarks for surplus division based on axiomatic principles but did not model the strategic process of negotiation. Rubinstein's key innovation was to incorporate time preference (discounting) and the threat of perpetual disagreement into a non-cooperative framework, yielding a unique subgame perfect equilibrium that reflects the strategic behavior of agents over time. In the model, the player who makes the first offer generally receives a larger share of the surplus, with the ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Evolutionary Game Theory
Evolutionary game theory (EGT) is the application of game theory to evolving populations in biology. It defines a framework of contests, strategies, and analytics into which Darwinism, Darwinian competition can be modelled. It originated in 1973 with John Maynard Smith and George R. Price's formalisation of contests, analysed as strategies, and the mathematical criteria that can be used to predict the results of competing strategies. Evolutionary game theory differs from classical game theory in focusing more on the dynamics of strategy change. This is influenced by the frequency of the competing strategies in the population. Evolutionary game theory has helped to explain the basis of altruism (biology), altruistic behaviours in Darwinian evolution. It has in turn become of interest to economists, sociologists, anthropologists, and philosophers. History Classical game theory Classical non-cooperative game theory was conceived by John von Neumann to determine optimal strategies i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Survival Function
The survival function is a function that gives the probability that a patient, device, or other object of interest will survive past a certain time. The survival function is also known as the survivor function or reliability function. The term ''reliability function'' is common in engineering while the term ''survival function'' is used in a broader range of applications, including human mortality. The survival function is the complementary cumulative distribution function of the lifetime. Sometimes complementary cumulative distribution functions are called survival functions in general. Definition Let the lifetime T be a continuous random variable describing the time to failure. If T has cumulative distribution function F(t) and probability density function f(t) on the interval [0,\infty), then the ''survival function'' or ''reliability function'' is: S(t) = P(T > t) = 1-F(t) = 1 - \int_0^t f(u)\,du Examples of survival functions The graphs below show examples of hypot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mixed Strategies
In game theory, a move, action, or play is any one of the options which a player can choose in a setting where the optimal outcome depends ''not only'' on their own actions ''but'' on the actions of others. The discipline mainly concerns the action of a player in a game affecting the behavior or actions of other players. Some examples of "games" include chess, bridge, poker, monopoly, diplomacy or battleship. The term strategy is typically used to mean a complete algorithm for playing a game, telling a player what to do for every possible situation. A player's strategy determines the action the player will take at any stage of the game. However, the idea of a strategy is often confused or conflated with that of a move or action, because of the correspondence between moves and pure strategies in most games: for any move ''X'', "always play move ''X''" is an example of a valid strategy, and as a result every move can also be considered to be a strategy. Other authors treat strateg ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subgame Perfect
In game theory, a subgame perfect equilibrium (SPE), or subgame perfect Nash equilibrium (SPNE), is a refinement of the Nash equilibrium concept, specifically designed for dynamic games where players make sequential decisions. A strategy profile is an SPE if it represents a Nash equilibrium in every possible subgame of the original game. Informally, this means that at any point in the game, the players' behavior from that point onward should represent a Nash equilibrium of the continuation game (i.e. of the subgame), no matter what happened before. This ensures that strategies are credible and rational throughout the entire game, eliminating non-credible threats. Every finite extensive game with complete information (all players know the complete state of the game) and perfect recall (each player remembers all their previous actions and knowledge throughout the game) has a subgame perfect equilibrium. A common method for finding SPE in finite games is backward induction, wher ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Maynard Smith
John Maynard Smith (6 January 1920 – 19 April 2004) was a British mathematical and theoretical biology, theoretical and mathematical evolutionary biologist and geneticist. Originally an aeronautical engineer during the Second World War, he took a second degree in genetics under the biologist J. B. S. Haldane. Maynard Smith was instrumental in the application of game theory to evolution with George R. Price, and theorised on other problems such as the evolution of sex and signalling theory. Biography Early years John Maynard Smith was born in London, the son of the surgeon Sidney Maynard Smith, but following his father's death in 1928, the family moved to Exmoor, where he became interested in natural history. Quite unhappy with the lack of formal science education at Eton College, Maynard Smith took it upon himself to develop an interest in Darwinism, Darwinian evolutionary theory and mathematics, after having read the work of old Etonian J. B. S. Haldane, whose books were ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nash Equilibria
In game theory, the Nash equilibrium is the most commonly used solution concept for non-cooperative games. A Nash equilibrium is a situation where no player could gain by changing their own strategy (holding all other players' strategies fixed). The idea of Nash equilibrium dates back to the time of Cournot, who in 1838 applied it to his model of competition in an oligopoly. If each player has chosen a strategy an action plan based on what has happened so far in the game and no one can increase one's own expected payoff by changing one's strategy while the other players keep theirs unchanged, then the current set of strategy choices constitutes a Nash equilibrium. If two players Alice and Bob choose strategies A and B, (A, B) is a Nash equilibrium if Alice has no other strategy available that does better than A at maximizing her payoff in response to Bob choosing B, and Bob has no other strategy available that does better than B at maximizing his payoff in response to Alice ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |