|
Vorticity Equation
The vorticity equation of fluid dynamics describes the evolution of the vorticity of a particle of a fluid dynamics, fluid as it moves with its flow (fluid), flow; that is, the local rotation of the fluid (in terms of vector calculus this is the curl (mathematics), curl of the flow velocity). The governing equation is:where is the material derivative operator, is the flow velocity, is the local fluid density, is the local pressure, is the viscous stress tensor and represents the sum of the external body forces. The first source term on the right hand side represents vortex stretching. The equation is valid in the absence of any concentrated torques and line forces for a Compressibility, compressible, Newtonian fluid. In the case of incompressible flow (i.e., low Mach number) and isotropic fluids, with conservative force, conservative body forces, the equation simplifies to the vorticity transport equation: :\frac = \left(\boldsymbol \cdot \nabla\right) \mathbf + \nu \nabla^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Dynamics
In physics, physical chemistry and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids – liquids and gases. It has several subdisciplines, including (the study of air and other gases in motion) and (the study of water and other liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moment (physics), moments on aircraft, determining the mass flow rate of petroleum through pipeline transport, pipelines, weather forecasting, predicting weather patterns, understanding nebulae in interstellar space, understanding large scale Geophysical fluid dynamics, geophysical flows involving oceans/atmosphere and Nuclear weapon design, modelling fission weapon detonation. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isotropic
In physics and geometry, isotropy () is uniformity in all orientations. Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence '' anisotropy''. ''Anisotropy'' is also used to describe situations where properties vary systematically, dependent on direction. Isotropic radiation has the same intensity regardless of the direction of measurement, and an isotropic field exerts the same action regardless of how the test particle is oriented. Mathematics Within mathematics, ''isotropy'' has a few different meanings: ; Isotropic manifolds: A manifold is isotropic if the geometry on the manifold is the same regardless of direction. A similar concept is homogeneity. ; Isotropic quadratic form: A quadratic form ''q'' is said to be isotropic if there is a non-zero vector ''v'' such that ; such a ''v'' is an isotropic vector or null vector. In complex geometry, a line through the origin in the direction of an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Surface Tension
Surface tension is the tendency of liquid surfaces at rest to shrink into the minimum surface area possible. Surface tension (physics), tension is what allows objects with a higher density than water such as razor blades and insects (e.g. Gerridae, water striders) to float on a water surface without becoming even partly submerged. At liquid–air interfaces, surface tension results from the greater attraction of liquid molecules to each other (due to Cohesion (chemistry), cohesion) than to the molecules in the air (due to adhesion). There are two primary mechanisms in play. One is an inward force on the surface molecules causing the liquid to contract. Second is a tangential force parallel to the surface of the liquid. This ''tangential'' force is generally referred to as the surface tension. The net effect is the liquid behaves as if its surface were covered with a stretched elastic membrane. But this analogy must not be taken too far as the tension in an elastic membrane i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electromagnetic Force
In physics, electromagnetism is an interaction that occurs between particles with electric charge via electromagnetic fields. The electromagnetic force is one of the four fundamental forces of nature. It is the dominant force in the interactions of atoms and molecules. Electromagnetism can be thought of as a combination of electrostatics and magnetism, which are distinct but closely intertwined phenomena. Electromagnetic forces occur between any two charged particles. Electric forces cause an attraction between particles with opposite charges and repulsion between particles with the same charge, while magnetism is an interaction that occurs between charged particles in relative motion. These two forces are described in terms of electromagnetic fields. Macroscopic charged objects are described in terms of Coulomb's law for electricity and Ampère's force law for magnetism; the Lorentz force describes microscopic charged particles. The electromagnetic force is responsible fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gravity
In physics, gravity (), also known as gravitation or a gravitational interaction, is a fundamental interaction, a mutual attraction between all massive particles. On Earth, gravity takes a slightly different meaning: the observed force between objects and the Earth. This force is dominated by the combined gravitational interactions of particles but also includes effect of the Earth's rotation. Gravity gives weight to physical objects and is essential to understanding the mechanisms responsible for surface water waves and lunar tides. Gravity also has many important biological functions, helping to guide the growth of plants through the process of gravitropism and influencing the circulation of fluids in multicellular organisms. The gravitational attraction between primordial hydrogen and clumps of dark matter in the early universe caused the hydrogen gas to coalesce, eventually condensing and fusing to form stars. At larger scales this results in galaxies and clust ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Baroclinity
In fluid dynamics, the baroclinity (often called baroclinicity) of a stratified fluid is a measure of how misaligned the gradient of pressure is from the gradient of density in a fluid. In meteorology, a baroclinic flow is one in which the density depends on both temperature and pressure (the fully general case). A simpler case, barotropic flow, allows for density dependence only on pressure, so that the Curl (mathematics), curl of the pressure-gradient force vanishes. Baroclinity is proportional to: :\nabla p \times \nabla \rho which is proportional to the sine of the angle between surfaces of constant pressure and surfaces of constant density. Thus, in a ''barotropic'' fluid (which is defined by zero baroclinity), these surfaces are parallel. In Earth's atmosphere, barotropic flow is a better approximation in the tropics, where density surfaces and pressure surfaces are both nearly level, whereas in higher latitudes the flow is more baroclinic. These midlatitude belts of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Specific Volume
In thermodynamics, the specific volume of a substance (symbol: , nu) is the quotient of the substance's volume () to its mass (): :\nu = \frac It is a mass-specific intrinsic property of the substance. It is the reciprocal of density (rho) and it is also related to the molar volume and molar mass: :\nu = \rho^ = \frac The standard unit of specific volume is cubic meters per kilogram (m3/kg), but other units include ft3/lb, ft3/slug, or mL/g. Specific volume for an ideal gas is related to the molar gas constant () and the gas's temperature (), pressure (), and molar mass (): : \nu = \frac It's based on the ideal gas law, PV = , and the amount of substance In chemistry, the amount of substance (symbol ) in a given sample of matter is defined as a ratio () between the particle number, number of elementary entities () and the Avogadro constant (). The unit of amount of substance in the International ..., n = m/M Applications Specific volume is commonly applied to: * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuity Equation
A continuity equation or transport equation is an equation that describes the transport of some quantity. It is particularly simple and powerful when applied to a conserved quantity, but it can be generalized to apply to any extensive quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described using continuity equations. Continuity equations are a stronger, local form of conservation laws. For example, a weak version of the law of conservation of energy states that energy can neither be created nor destroyed—i.e., the total amount of energy in the universe is fixed. This statement does not rule out the possibility that a quantity of energy could disappear from one point while simultaneously appearing at another point. A stronger statement is that energy is ''locally'' conserved: energy can neither be created nor destroyed, ''nor'' can it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
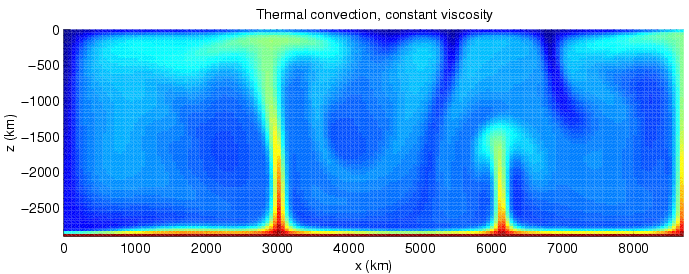
Convection
Convection is single or Multiphase flow, multiphase fluid flow that occurs Spontaneous process, spontaneously through the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoyancy). When the cause of the convection is unspecified, convection due to the effects of thermal expansion and buoyancy can be assumed. Convection may also take place in soft solids or mixtures where particles can flow. Convective flow may be Transient state, transient (such as when a Multiphasic liquid, multiphase mixture of oil and water separates) or steady state (see convection cell). The convection may be due to Gravity, gravitational, Electromagnetism, electromagnetic or Fictitious force, fictitious body forces. Convection (heat transfer), Heat transfer by natural convection plays a role in the structure of Earth's atmosphere, its oceans, and its Earth's mantle, mantle. Discrete convective cells in the atmosphere can be identified by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steady State Flow
Steady may refer to: * Steady state, a concept used in math and sciences where variables are time-constant * Steady flow, a condition of flow that does not change with time * ''Steady'', a 2006 album by Jim Bianco * ''Steady'' (album), a 2022 album by Sloan * "Steady", a 2018 song by Bebe Rexha featuring Tory Lanez from the album '' Expectations'' * Steady web and mobile app See also * Steady state (other) Steady state may refer to: *Steady state (systems) an operating condition in thermodynamic and other systems or processes when variables stay constant as time passes. **Steady-state economy, an economy made up of a constant population size and a con ... * Unsteady (other) {{disambiguation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Substantive Derivative
In continuum mechanics, the material derivative describes the time rate of change of some physical quantity (like heat or momentum) of a material element that is subjected to a space-and-time-dependent macroscopic velocity field. The material derivative can serve as a link between Eulerian and Lagrangian descriptions of continuum deformation. For example, in fluid dynamics, the velocity field is the flow velocity, and the quantity of interest might be the temperature of the fluid. In this case, the material derivative then describes the temperature change of a certain fluid parcel with time, as it flows along its pathline (trajectory). Other names There are many other names for the material derivative, including: *advective derivative *convective derivative *derivative following the motion *hydrodynamic derivative *Lagrangian derivative *particle derivative *substantial derivative *substantive derivative *Stokes derivative *total derivative, although the material derivati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |