|
Vorticity Confinement
Vorticity confinement (VC), a physics-based computational fluid dynamics model analogous to shock capturing methods, was invented by Dr. John Steinhoff, professor at the University of Tennessee Space Institute, in the late 1980s to solve vortex dominated flows. It was first formulated to capture concentrated vortices shed from the wings, and later became popular in a wide range of research areas. During the 1990s and 2000s, it became widely used in the field of engineering. The method VC has a basic familiarity to soliton, solitary wave approach which is extensively used in many condensed matter physics applications. The effect of VC is to capture the small scale features over as few as 2 grid cells as they convect through the flow. The basic idea is similar to that of compression discontinuity (mathematics), discontinuity in Eulerian shock capturing methods. The internal structure is maintained thin and so the details of the internal structure may not be important. Example Conside ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Fluid Dynamics
Computational fluid dynamics (CFD) is a branch of fluid mechanics that uses numerical analysis and data structures to analyze and solve problems that involve fluid flows. Computers are used to perform the calculations required to simulate the free-stream flow of the fluid, and the interaction of the fluid ( liquids and gases) with surfaces defined by boundary conditions. With high-speed supercomputers, better solutions can be achieved, and are often required to solve the largest and most complex problems. Ongoing research yields software that improves the accuracy and speed of complex simulation scenarios such as transonic or turbulent flows. Initial validation of such software is typically performed using experimental apparatus such as wind tunnels. In addition, previously performed analytical or empirical analysis of a particular problem can be used for comparison. A final validation is often performed using full-scale testing, such as flight tests. CFD is appli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dissipation
In thermodynamics, dissipation is the result of an irreversible process that takes place in homogeneous thermodynamic systems. In a dissipative process, energy (internal, bulk flow kinetic, or system potential) transforms from an initial form to a final form, where the capacity of the final form to do thermodynamic work is less than that of the initial form. For example, heat transfer is dissipative because it is a transfer of internal energy from a hotter body to a colder one. Following the second law of thermodynamics, the entropy varies with temperature (reduces the capacity of the combination of the two bodies to do work), but never decreases in an isolated system. These processes produce entropy at a certain rate. The entropy production rate times ambient temperature gives the dissipated power. Important examples of irreversible processes are: heat flow through a thermal resistance, fluid flow through a flow resistance, diffusion (mixing), chemical reactions, and elec ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Without VC '', 2021
{{disambiguation ...
Without may refer to: * "Without" (''The X-Files''), an episode in the eighth season of ''The X-Files'' * "without", an English preposition * "Without", a film that premiered at the 2011 Slamdance Film Festival * "Without", a song by Jack Savoretti from the album ''Between the Minds'', 2007 * "Without", a song by Brett Kissel from the album ''What Is Life? ''What Is Life? The Physical Aspect of the Living Cell'' is a 1944 science book written for the lay reader by physicist Erwin Schrödinger. The book was based on a course of public lectures delivered by Schrödinger in February 1943, under the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
With VC , a ...
With or WITH may refer to: * With, a preposition in English * Carl Johannes With (1877–1923), Danish doctor and arachnologist * With (character), a character in ''D. N. Angel'' * ''With'' (novel), a novel by Donald Harrington * ''With'' (album), a 2014 album by TVXQ * ''With'' (EP), a 2021 EP by Nam Woo-hyun Radio stations * WITH (FM), a radio station (90.1 FM) licensed to Ithaca, New York, United States * WRBS (AM), a radio station (1230 AM) licensed to Baltimore, Maryland, United States, which used the call sign WITH from 1941 until 2006 * WZFT, a radio station (104.3 FM) licensed to Baltimore, Maryland, United States, which used the call sign WITH-FM from 1949 until 1974 Places * Woodlands Integrated Transport Hub Woodlands Bus Interchange (formerly Woodlands Regional Bus Interchange) is a bus interchange in Singapore. Located at Woodlands, the interchange is linked to Woodlands MRT station and adjacent to Causeway Point shopping mall. It is the largest ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Confinement
In physics, mathematics, and related fields, a wave is a propagating dynamic disturbance (change from equilibrium) of one or more quantities. Waves can be periodic, in which case those quantities oscillate repeatedly about an equilibrium (resting) value at some frequency. When the entire waveform moves in one direction, it is said to be a ''traveling wave''; by contrast, a pair of superimposed periodic waves traveling in opposite directions makes a ''standing wave''. In a standing wave, the amplitude of vibration has nulls at some positions where the wave amplitude appears smaller or even zero. Waves are often described by a ''wave equation'' (standing wave field of two opposite waves) or a one-way wave equation for single wave propagation in a defined direction. Two types of waves are most commonly studied in classical physics. In a ''mechanical wave'', stress and strain fields oscillate about a mechanical equilibrium. A mechanical wave is a local deformation (strain) in so ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wave Equation
The (two-way) wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields — as they occur in classical physics — such as mechanical waves (e.g. water waves, sound waves and seismic waves) or electromagnetic waves (including light waves). It arises in fields like acoustics, electromagnetism, and fluid dynamics. Single mechanical or electromagnetic waves propagating in a pre-defined direction can also be described with the first-order one-way wave equation which is much easier to solve and also valid for inhomogenious media. Introduction The (two-way) wave equation is a second-order partial differential equation describing waves, including traveling and standing waves; the latter can be considered as linear superpositions of waves traveling in opposite directions. This article mostly focuses on the scalar wave equation describing waves in scalars by scalar functions of a time variable (a variable repres ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vorticity
In continuum mechanics, vorticity is a pseudovector field that describes the local spinning motion of a continuum near some point (the tendency of something to rotate), as would be seen by an observer located at that point and traveling along with the flow. It is an important quantity in the dynamical theory of fluids and provides a convenient framework for understanding a variety of complex flow phenomena, such as the formation and motion of vortex rings. Mathematically, the vorticity \vec is the curl of the flow velocity \vec: :\vec \equiv \nabla \times \vec\,, where \nabla is the nabla operator. Conceptually, \vec could be determined by marking parts of a continuum in a small neighborhood of the point in question, and watching their ''relative'' displacements as they move along the flow. The vorticity \vec would be twice the mean angular velocity vector of those particles relative to their center of mass, oriented according to the right-hand rule. In a two-dimensiona ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Velocity
Velocity is the directional speed of an object in motion as an indication of its rate of change in position as observed from a particular frame of reference and as measured by a particular standard of time (e.g. northbound). Velocity is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of bodies. Velocity is a physical vector quantity; both magnitude and direction are needed to define it. The scalar absolute value ( magnitude) of velocity is called , being a coherent derived unit whose quantity is measured in the SI ( metric system) as metres per second (m/s or m⋅s−1). For example, "5 metres per second" is a scalar, whereas "5 metres per second east" is a vector. If there is a change in speed, direction or both, then the object is said to be undergoing an ''acceleration''. Constant velocity vs acceleration To have a ''constant velocity'', an object must have a constant speed in a constant direction. Constant dire ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
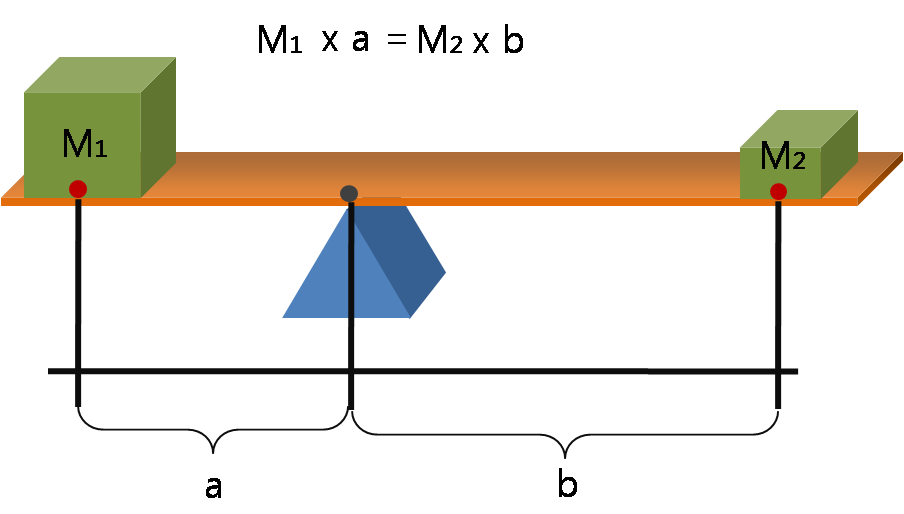
Moment (physics)
In physics, a moment is a mathematical expression involving the product of a distance and physical quantity. Moments are usually defined with respect to a fixed reference point and refer to physical quantities located some distance from the reference point. In this way, the moment accounts for the quantity's location or arrangement. For example, the moment of force, often called torque, is the product of a force on an object and the distance from the reference point to the object. In principle, any physical quantity can be multiplied by a distance to produce a moment. Commonly used quantities include forces, masses, and electric charge distributions. Elaboration In its most basic form, a moment is the product of the distance to a point, raised to a power, and a physical quantity (such as force or electrical charge) at that point: : \mu_n = r^n\,Q, where Q is the physical quantity such as a force applied at a point, or a point charge, or a point mass, etc. If the quantity ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equation
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function. The function is often thought of as an "unknown" to be solved for, similarly to how is thought of as an unknown number to be solved for in an algebraic equation like . However, it is usually impossible to write down explicit formulas for solutions of partial differential equations. There is, correspondingly, a vast amount of modern mathematical and scientific research on methods to numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such as existence, uniqueness, regularity, and stability. Among the many open questions are the e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shock Capturing Methods
In computational fluid dynamics, shock-capturing methods are a class of techniques for computing inviscid flows with shock waves. The computation of flow containing shock waves is an extremely difficult task because such flows result in sharp, discontinuous changes in flow variables such as pressure, temperature, density, and velocity across the shock. Method In shock-capturing methods, the governing equations of inviscid flows (i.e. Euler equations) are cast in conservation form and any shock waves or discontinuities are computed as part of the solution. Here, no special treatment is employed to take care of the shocks themselves, which is in contrast to the shock-fitting method, where shock waves are explicitly introduced in the solution using appropriate shock relations ( Rankine–Hugoniot relations). The shock waves predicted by shock-capturing methods are generally not sharp and may be smeared over several grid elements. Also, classical shock-capturing methods have the disadvan ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler Equations
200px, Leonhard Euler (1707–1783) In mathematics and physics, many topics are named in honor of Swiss mathematician Leonhard Euler (1707–1783), who made many important discoveries and innovations. Many of these items named after Euler include their own unique function, equation, formula, identity, number (single or sequence), or other mathematical entity. Many of these entities have been given simple and ambiguous names such as Euler's function, Euler's equation, and Euler's formula. Euler's work touched upon so many fields that he is often the earliest written reference on a given matter. In an effort to avoid naming everything after Euler, some discoveries and theorems are attributed to the first person to have proved them ''after'' Euler. Conjectures * Euler's conjecture (Waring's problem) *Euler's sum of powers conjecture * Euler's Graeco-Latin square conjecture Equations Usually, ''Euler's equation'' refers to one of (or a set of) differential equations (DEs). It is c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |