|
Vigesimal
vigesimal () or base-20 (base-score) numeral system is based on twenty (in the same way in which the decimal numeral system is based on ten). '' Vigesimal'' is derived from the Latin adjective '' vicesimus'', meaning 'twentieth'. Places In a vigesimal place system, twenty individual numerals (or digit symbols) are used, ten more than in the usual decimal system. One modern method of finding the extra needed symbols is to write ten as the letter (the 20 means base ), to write nineteen as , and the numbers between with the corresponding letters of the alphabet. This is similar to the common computer-science practice of writing hexadecimal numerals over 9 with the letters "A–F". Another less common method skips over the letter "I", in order to avoid confusion between I20 as eighteen and one, so that the number eighteen is written as J20, and nineteen is written as K20. The number twenty is written as . According to this notation: : is equivalent to forty in decimal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
20 (number)
20 (twenty; Roman numeral XX) is the natural number following 19 (number), 19 and preceding 21 (number), 21. A group of twenty units may also be referred to as a score. In mathematics *20 is a pronic number. *20 is a tetrahedral number as 1, 4, 10, 20. *20 is the basis for vigesimal number systems. *20 is the third composite number to be the product of a squared prime and a prime, and also the second member of the (''2''2)''q'' family in this form. *20 is the smallest primitive abundant number. *An icosahedron has 20 faces. A dodecahedron has 20 vertices. *20 can be written as the sum of three Fibonacci numbers uniquely, i.e. 20 = 13 + 5 + 2. *20 is the number of moves (quarter or half turns) required to optimally solve a Rubik's Cube in the worst case. (e.g. the newspaper headline "Scores of Typhoon Survivors Flown to Manila")."CBS News"''Scores of Typhoon Survivors Flown to Manila'' (November 2013) In sports * Twenty20 is a form of limited overs cricket where each team ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radix
In a positional numeral system, the radix or base is the number of unique digits, including the digit zero, used to represent numbers. For example, for the decimal/denary system (the most common system in use today) the radix (base number) is ten, because it uses the ten digits from 0 through 9. In any standard positional numeral system, a number is conventionally written as with ''x'' as the string of digits and ''y'' as its base, although for base ten the subscript is usually assumed (and omitted, together with the pair of parentheses), as it is the most common way to express value. For example, (the decimal system is implied in the latter) and represents the number one hundred, while (100)2 (in the binary system with base 2) represents the number four. Etymology ''Radix'' is a Latin word for "root". ''Root'' can be considered a synonym for ''base,'' in the arithmetical sense. In numeral systems In the system with radix 13, for example, a string of digits such as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Root Of 3
The square root of 3 is the positive real number that, when multiplied by itself, gives the number 3. It is denoted mathematically as \sqrt or 3^. It is more precisely called the principal square root of 3 to distinguish it from the negative number with the same property. The square root of 3 is an irrational number. It is also known as Theodorus' constant, after Theodorus of Cyrene, who proved its irrationality. , its numerical value in decimal notation had been computed to at least ten billion digits. Its decimal expansion, written here to 65 decimal places, is given by : : The fraction \frac (...) can be used as a good approximation. Despite having a denominator of only 56, it differs from the correct value by less than \frac (approximately 9.2\times 10^, with a relative error of 5\times 10^). The rounded value of is correct to within 0.01% of the actual value. The fraction \frac (...) is accurate to 1\times 10^. Archimedes reported a range for its value: (\frac)^> ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Artin's Conjecture On Primitive Roots
In number theory, Artin's conjecture on primitive roots states that a given integer ''a'' that is neither a square number nor −1 is a primitive root modulo infinitely many primes ''p''. The conjecture also ascribes an asymptotic density to these primes. This conjectural density equals Artin's constant or a rational multiple thereof. The conjecture was made by Emil Artin to Helmut Hasse on September 27, 1927, according to the latter's diary. The conjecture is still unresolved as of 2022. In fact, there is no single value of ''a'' for which Artin's conjecture is proved. Formulation Let ''a'' be an integer that is not a square number and not −1. Write ''a'' = ''a''0''b''2 with ''a''0 square-free. Denote by ''S''(''a'') the set of prime numbers ''p'' such that ''a'' is a primitive root modulo ''p''. Then the conjecture states # ''S''(''a'') has a positive asymptotic density inside the set of primes. In particular, ''S''(''a'') is infinite. # Under the conditions ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cyclic Number
A cyclic number is an integer for which cyclic permutations of the digits are successive integer multiples of the number. The most widely known is the six-digit number 142857, whose first six integer multiples are :142857 × 1 = 142857 :142857 × 2 = 285714 :142857 × 3 = 428571 :142857 × 4 = 571428 :142857 × 5 = 714285 :142857 × 6 = 857142 Details To qualify as a cyclic number, it is required that consecutive multiples be cyclic permutations. Thus, the number 076923 would not be considered a cyclic number, because even though all cyclic permutations are multiples, they are not consecutive integer multiples: :076923 × 1 = 076923 :076923 × 3 = 230769 :076923 × 4 = 307692 :076923 × 9 = 692307 :076923 × 10 = 769230 :076923 × 12 = 923076 The following trivial cases are typically excluded: #single digits, e.g.: 5 #repeated digits, e.g.: 555 #repeated cyclic numbers, e.g.: 142857142857 If leading zeros are not ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Root Of 2
The square root of 2 (approximately 1.4142) is a positive real number that, when multiplied by itself, equals the number 2. It may be written in mathematics as \sqrt or 2^, and is an algebraic number. Technically, it should be called the principal square root of 2, to distinguish it from the negative number with the same property. Geometrically, the square root of 2 is the length of a diagonal across a square with sides of one unit of length; this follows from the Pythagorean theorem. It was probably the first number known to be irrational. The fraction (≈ 1.4142857) is sometimes used as a good rational approximation with a reasonably small denominator. Sequence in the On-Line Encyclopedia of Integer Sequences consists of the digits in the decimal expansion of the square root of 2, here truncated to 65 decimal places: : History The Babylonian clay tablet YBC 7289 (c. 1800–1600 BC) gives an approximation of in four sexagesimal figures, , which is accurate to a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diagonal
In geometry, a diagonal is a line segment joining two vertices of a polygon or polyhedron, when those vertices are not on the same edge. Informally, any sloping line is called diagonal. The word ''diagonal'' derives from the ancient Greek διαγώνιος ''diagonios'', "from angle to angle" (from διά- ''dia-'', "through", "across" and γωνία ''gonia'', "angle", related to ''gony'' "knee"); it was used by both Strabo and Euclid to refer to a line connecting two vertices of a rhombus or cuboid, and later adopted into Latin as ''diagonus'' ("slanting line"). In matrix algebra, the diagonal of a square matrix consists of the entries on the line from the top left corner to the bottom right corner. There are also other, non-mathematical uses. Non-mathematical uses In engineering, a diagonal brace is a beam used to brace a rectangular structure (such as scaffolding) to withstand strong forces pushing into it; although called a diagonal, due to practical consid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square (geometry)
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adjacent sides. It is the only regular polygon whose internal angle, central angle, and external angle are all equal (90°), and whose diagonals are all equal in length. A square with vertices ''ABCD'' would be denoted . Characterizations A convex quadrilateral is a square if and only if it is any one of the following: * A rectangle with two adjacent equal sides * A rhombus with a right vertex angle * A rhombus with all angles equal * A parallelogram with one right vertex angle and two adjacent equal sides * A quadrilateral with four equal sides and four right angles * A quadrilateral where the diagonals are equal, and are the perpendicular bisectors of each other (i.e., a rhombus with equal diagonals) * A convex quadrilateral w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Maya
Maya may refer to: Civilizations * Maya peoples, of southern Mexico and northern Central America ** Maya civilization, the historical civilization of the Maya peoples ** Maya language, the languages of the Maya peoples * Maya (Ethiopia), a population native to the old Wej province in Ethiopia Places * Maya (river), a river in Yakutia, Russia * Maya (Uda), a river in Khabarovsk Krai, Russia * Maya, Uganda, a town * Maya, Western Australia, a town * Maya Karimata, an island in West Borneo, Indonesia * Maya Mountains, a mountain range in Guatemala and Belize ** Maya Biosphere Reserve, a nature reservation in Guatemala * Mount Maya, a mountain in Kobe, Japan ** Maya Station, a railway station in Kobe, Japan * La Maya (mountain), an alp in Switzerland * Al Maya or Maya, a town in Libya Religion and mythology * Maya religion, the religious practices of the Maya peoples of parts of Mexico and Central America ** Maya mythology, the myths and legends of the Maya civilizatio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only regular hexahedron and is one of the five Platonic solids. It has 6 faces, 12 edges, and 8 vertices. The cube is also a square parallelepiped, an equilateral cuboid and a right rhombohedron a 3- zonohedron. It is a regular square prism in three orientations, and a trigonal trapezohedron in four orientations. The cube is dual to the octahedron. It has cubical or octahedral symmetry. The cube is the only convex polyhedron whose faces are all squares. Orthogonal projections The ''cube'' has four special orthogonal projections, centered, on a vertex, edges, face and normal to its vertex figure. The first and third correspond to the A2 and B2 Coxeter planes. Spherical tiling The cube can also be represented as a spheric ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
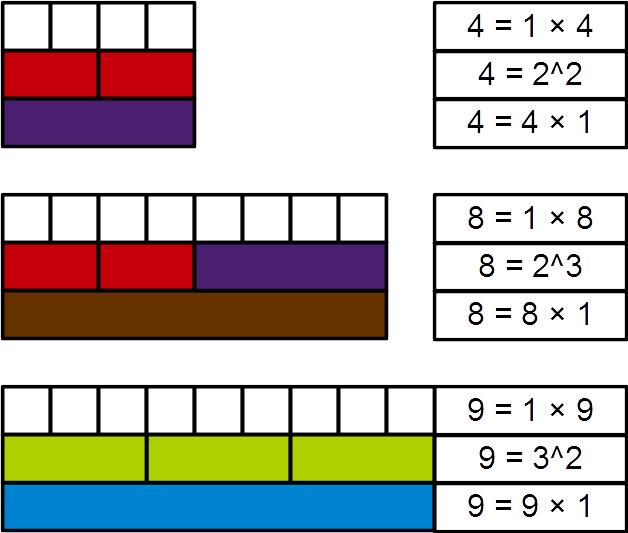
Perfect Power
In mathematics, a perfect power is a natural number that is a product of equal natural factors, or, in other words, an integer that can be expressed as a square or a higher integer power of another integer greater than one. More formally, ''n'' is a perfect power if there exist natural numbers ''m'' > 1, and ''k'' > 1 such that ''mk'' = ''n''. In this case, ''n'' may be called a perfect ''k''th power. If ''k'' = 2 or ''k'' = 3, then ''n'' is called a perfect square or perfect cube, respectively. Sometimes 0 and 1 are also considered perfect powers (0''k'' = 0 for any ''k'' > 0, 1''k'' = 1 for any ''k''). Examples and sums A sequence of perfect powers can be generated by iterating through the possible values for ''m'' and ''k''. The first few ascending perfect powers in numerical order (showing duplicate powers) are : : 2^2 = 4,\ 2^3 = 8,\ 3^2 = 9,\ 2^4 = 16,\ 4^2 = 16,\ 5^2 = 25,\ 3^3 = 27, 2^5 = 32,\ 6^2 = 36,\ 7^2 = 49,\ 2^6 = 64,\ 4^3 = 64,\ 8^2 = 64, \dots The sum of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |