|
Vibration Of Plates
The vibration of plates is a special case of the more general problem of mechanical vibrations. The equations governing the motion of plates are simpler than those for general three-dimensional objects because one of the dimensions of a plate is much smaller than the other two. This permits a two-dimensional plate theory to give an excellent approximation to the actual three-dimensional motion of a plate-like object.Reddy, J. N., 2007, Theory and analysis of elastic plates and shells, CRC Press, Taylor and Francis. There are several theories that have been developed to describe the motion of plates. The most commonly used are the Kirchhoff-Love theory and the Uflyand-Mindlin. The latter theory is discussed in detail by Elishakoff. Solutions to the governing equations predicted by these theories can give us insight into the behavior of plate-like objects both under free and forced conditions. This includes the propagation of waves and the study of standing waves and vibration ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamilton's Principle
In physics, Hamilton's principle is William Rowan Hamilton's formulation of the principle of stationary action. It states that the dynamics of a physical system are determined by a variational problem for a functional based on a single function, the Lagrangian, which may contain all physical information concerning the system and the forces acting on it. The variational problem is equivalent to and allows for the derivation of the '' differential'' equations of motion of the physical system. Although formulated originally for classical mechanics, Hamilton's principle also applies to classical fields such as the electromagnetic and gravitational fields, and plays an important role in quantum mechanics, quantum field theory and criticality theories. Mathematical formulation Hamilton's principle states that the true evolution of a system described by generalized coordinates between two specified states and at two specified times and is a stationary point (a point where ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mindlin–Reissner Plate Theory
The Reissner–Mindlin theory of plates is an extension of Kirchhoff–Love plate theory that takes into account shear deformations through-the-thickness of a plate. The theory was proposed in 1951 by Raymond Mindlin. A similar, but not identical, theory in static setting, had been proposed earlier by Eric Reissner in 1945. Both theories are intended for thick plates in which the normal to the mid-surface remains straight but not necessarily perpendicular to the mid-surface. The Reissner-Mindlin theory is used to calculate the deformations and stresses in a plate whose thickness is of the order of one tenth the planar dimensions while the Kirchhoff–Love theory is applicable to thinner plates. The form of Reissner-Mindlin plate theory that is most commonly used is actually due to Mindlin and is more properly called ''Mindlin plate theory''. The Reissner theory is slightly different. Both theories include in-plane shear strains and both are extensions of Kirchhoff–Love ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Elasticity
Linear elasticity is a mathematical model of how solid objects deform and become internally stressed by prescribed loading conditions. It is a simplification of the more general nonlinear theory of elasticity and a branch of continuum mechanics. The fundamental assumptions of linear elasticity are infinitesimal strains — meaning, "small" deformations — and linear relationships between the components of stress and strain — hence the "linear" in its name. Linear elasticity is valid only for stress states that do not produce yielding. Its assumptions are reasonable for many engineering materials and engineering design scenarios. Linear elasticity is therefore used extensively in structural analysis and engineering design, often with the aid of finite element analysis. Mathematical formulation Equations governing a linear elastic boundary value problem are based on three tensor partial differential equations for the balance of linear momentum and six in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infinitesimal Strain Theory
In continuum mechanics, the infinitesimal strain theory is a mathematical approach to the description of the deformation of a solid body in which the displacements of the material particles are assumed to be much smaller (indeed, infinitesimally smaller) than any relevant dimension of the body; so that its geometry and the constitutive properties of the material (such as density and stiffness) at each point of space can be assumed to be unchanged by the deformation. With this assumption, the equations of continuum mechanics are considerably simplified. This approach may also be called small deformation theory, small displacement theory, or small displacement-gradient theory. It is contrasted with the finite strain theory where the opposite assumption is made. The infinitesimal strain theory is commonly adopted in civil and mechanical engineering for the stress analysis of structures built from relatively stiff elastic materials like concrete and steel, since a common goal in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ernst Chladni
Ernst Florens Friedrich Chladni (, , ; 30 November 1756 – 3 April 1827) was a German physicist and musician. His most important work, for which he is sometimes labeled the father of acoustics, included research on vibrating plates and the calculation of the speed of sound for different gases. He also undertook pioneering work in the study of meteorites and is regarded by some as the father of meteoritics. Early life Although Chladni was born in Wittenberg in Saxony, his family originated from Kremnica, then part of the Kingdom of Hungary and today a mining town in central Slovakia. Chladni has therefore been identified as German, Hungarian and Slovak. Chladni came from an educated family of academics and learned men. Chladni's great-grandfather, the Lutheran clergyman Georg Chladni (1637–1692), had left Kremnica in 1673 during the Counter Reformation. Chladni's grandfather, Martin Chladni (1669–1725), was also a Lutheran theologian and, in 1710, became profess ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bending Of Plates
Bending of plates, or plate bending, refers to the deflection of a plate perpendicular to the plane of the plate under the action of external forces and moments. The amount of deflection can be determined by solving the differential equations of an appropriate plate theory. The stresses in the plate can be calculated from these deflections. Once the stresses are known, failure theories can be used to determine whether a plate will fail under a given load. Bending of Kirchhoff-Love plates Definitions For a thin rectangular plate of thickness H, Young's modulus E, and Poisson's ratio \nu, we can define parameters in terms of the plate deflection, w. The flexural rigidity is given by : D = \frac Moments The bending moments per unit length are given by : M_ = -D \left( \frac + \nu \frac \right) : M_ = -D \left( \nu \frac + \frac \right) The twisting moment per unit length is given by : M_ = -D \left( 1 - \nu \right) \frac Forces The shear fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bending
In applied mechanics, bending (also known as flexure) characterizes the behavior of a slender structural element subjected to an external Structural load, load applied perpendicularly to a longitudinal axis of the element. The structural element is assumed to be such that at least one of its dimensions is a small fraction, typically 1/10 or less, of the other two.Boresi, A. P. and Schmidt, R. J. and Sidebottom, O. M., 1993, Advanced mechanics of materials, John Wiley and Sons, New York. When the length is considerably longer than the width and the thickness, the element is called a Beam (structure), beam. For example, a closet rod Deflection (engineering), sagging under the weight of clothes on clothes hangers is an example of a beam experiencing bending. On the other hand, a wikt:shell, shell is a structure of any geometric form where the length and the width are of the same order of magnitude but the thickness of the structure (known as the 'wall') is considerably smaller. A l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Biharmonic
In mathematics, the biharmonic equation is a fourth-order partial differential equation which arises in areas of continuum mechanics, including linear elasticity theory and the solution of Stokes flows. Specifically, it is used in the modeling of thin structures that react elastically to external forces. Notation It is written as \nabla^4 \varphi = 0 or \nabla^2 \nabla^2 \varphi = 0 or \Delta^2 \varphi = 0 where \nabla^4, which is the fourth power of the del operator and the square of the Laplacian operator \nabla^2 (or \Delta), is known as the biharmonic operator or the bilaplacian operator. In Cartesian coordinates, it can be written in n dimensions as: \nabla^4 \varphi = \sum_^n\sum_^n \partial_i\partial_i\partial_j\partial_j \varphi = \left(\sum_^n \partial_i\partial_i\right) \left(\sum_^n \partial_j\partial_j\right) \varphi. Because the formula here contains a summation of indices, many mathematicians prefer the notation \Delta^2 over \nabla^4 because the former makes cle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
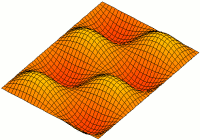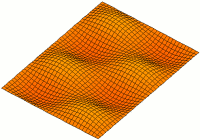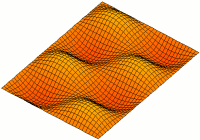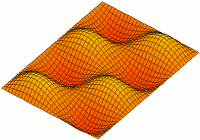
Two Dim Standing Wave
2 (two) is a number, numeral and digit. It is the natural number following 1 and preceding 3. It is the smallest and the only even prime number. Because it forms the basis of a duality, it has religious and spiritual significance in many cultures. Mathematics The number 2 is the second natural number after 1. Each natural number, including 2, is constructed by succession, that is, by adding 1 to the previous natural number. 2 is the smallest and the only even prime number, and the first Ramanujan prime. It is also the first superior highly composite number, and the first colossally abundant number. An integer is determined to be even if it is divisible by two. When written in base 10, all multiples of 2 will end in 0, 2, 4, 6, or 8; more generally, in any even base, even numbers will end with an even digit. A digon is a polygon with two sides (or edges) and two vertices. Two distinct points in a plane are always sufficient to define a unique line in a nontrivial ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Modified Bessel Function
Bessel functions, named after Friedrich Bessel who was the first to systematically study them in 1824, are canonical solutions of Bessel's differential equation x^2 \frac + x \frac + \left(x^2 - \alpha^2 \right)y = 0 for an arbitrary complex number \alpha, which represents the ''order'' of the Bessel function. Although \alpha and -\alpha produce the same differential equation, it is conventional to define different Bessel functions for these two values in such a way that the Bessel functions are mostly smooth functions of \alpha. The most important cases are when \alpha is an integer or half-integer. Bessel functions for integer \alpha are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to Laplace's equation in cylindrical coordinates. #Spherical Bessel functions, Spherical Bessel functions with half-integer \alpha are obtained when solving the Helmholtz equation in spherical coordinates. Applications Bessel's equation arise ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bessel Function
Bessel functions, named after Friedrich Bessel who was the first to systematically study them in 1824, are canonical solutions of Bessel's differential equation x^2 \frac + x \frac + \left(x^2 - \alpha^2 \right)y = 0 for an arbitrary complex number \alpha, which represents the ''order'' of the Bessel function. Although \alpha and -\alpha produce the same differential equation, it is conventional to define different Bessel functions for these two values in such a way that the Bessel functions are mostly smooth functions of \alpha. The most important cases are when \alpha is an integer or half-integer. Bessel functions for integer \alpha are also known as cylinder functions or the cylindrical harmonics because they appear in the solution to Laplace's equation in cylindrical coordinates. Spherical Bessel functions with half-integer \alpha are obtained when solving the Helmholtz equation in spherical coordinates. Applications Bessel's equation arises when finding separa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |