|
Variation (astronomy)
In astronomy, the variation of the Moon is one of the principal perturbation (astronomy), perturbations in the motion of the Moon. Discovery The variation was discovered by Tycho Brahe, who noticed that, starting from a lunar eclipse in December 1590, at the times of Syzygy (astronomy), syzygy (new or full moon), the apparent velocity of motion of the Moon (along its orbit as seen against the background of stars) was faster than expected. On the other hand, at the times of first and last quarter, its velocity was correspondingly slower than expected. (Those expectations were based on the lunar tables widely used up to Tycho's time. They took some account of the two largest irregularities in the Moon's motion, i.e. those now known as the equation of the center and the evection, see also Lunar theory#History, Lunar theory - History.) Variation The main visible effect (in longitude) of the variation of the Moon is that during the course of every month, at the octants of the Moon's p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astronomy
Astronomy is a natural science that studies celestial objects and the phenomena that occur in the cosmos. It uses mathematics, physics, and chemistry in order to explain their origin and their overall evolution. Objects of interest include planets, natural satellite, moons, stars, nebulae, galaxy, galaxies, meteoroids, asteroids, and comets. Relevant phenomena include supernova explosions, gamma ray bursts, quasars, blazars, pulsars, and cosmic microwave background radiation. More generally, astronomy studies everything that originates beyond atmosphere of Earth, Earth's atmosphere. Cosmology is a branch of astronomy that studies the universe as a whole. Astronomy is one of the oldest natural sciences. The early civilizations in recorded history made methodical observations of the night sky. These include the Egyptian astronomy, Egyptians, Babylonian astronomy, Babylonians, Greek astronomy, Greeks, Indian astronomy, Indians, Chinese astronomy, Chinese, Maya civilization, M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ecliptic Longitude
In astronomy, the ecliptic coordinate system is a celestial coordinate system commonly used for representing the apparent positions, orbits, and pole orientations of Solar System objects. Because most planets (except Mercury) and many small Solar System bodies have orbits with only slight inclinations to the ecliptic, using it as the fundamental plane is convenient. The system's origin can be the center of either the Sun or Earth, its primary direction is towards the March equinox, and it has a right-hand convention. It may be implemented in spherical or rectangular coordinates. Primary direction The celestial equator and the ecliptic are slowly moving due to perturbing forces on the Earth, therefore the orientation of the primary direction, their intersection at the March equinox, is not quite fixed. A slow motion of Earth's axis, precession, causes a slow, continuous turning of the coordinate system westward about the poles of the ecliptic, completing one circuit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Celestial Mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of objects in outer space. Historically, celestial mechanics applies principles of physics (classical mechanics) to astronomical objects, such as stars and planets, to produce ephemeris data. History Modern analytic celestial mechanics started with Isaac Newton's ''Principia'' (1687). The name celestial mechanics is more recent than that. Newton wrote that the field should be called "rational mechanics". The term "dynamics" came in a little later with Gottfried Leibniz, and over a century after Newton, Pierre-Simon Laplace introduced the term ''celestial mechanics''. Prior to Kepler, there was little connection between exact, quantitative prediction of planetary positions, using geometrical or numerical techniques, and contemporary discussions of the physical causes of the planets' motion. Laws of planetary motion Johannes Kepler was the first to closely integrate the predictive geometrical a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ernest William Brown
Ernest William Brown FRS (29 November 1866 – 22 July 1938) was an English mathematician and astronomer, who spent the majority of his career working in the United States and became a naturalised American citizen in 1923. His life's work was the study of the Moon's motion (lunar theory) and the compilation of extremely accurate lunar tables. He also studied the motion of the planets and calculated the orbits of Trojan asteroids. Life and career Brown was born in Hull, England, the second of four children of William and Emma Brown (née Martin). His father was originally a farmer and later became a timber merchant. His mother and younger brother died of scarlet fever in 1870, when Brown was not quite 4 years old. He and his two sisters were then looked after by a maiden aunt, until his father remarried five years later. Education and early career Brown was educated at Totteridge Park School, Hertfordshire (now part of Dorset House School) anHull and East Riding College ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Evection
{{Main, Lunar theory In astronomy, evection (Latin for "carrying away") is the largest inequality produced by the action of the Sun in the monthly revolution of the Moon around the Earth. The evection, formerly called the moon's second anomaly, was approximately known in ancient times, and its discovery is attributed to Ptolemy. The current name itself dates much more recently, from the 17th century: it was coined by Bullialdus in connection with his own theory of the Moon's motion. Evection causes the Moon's ecliptic longitude to vary by approximately ± 1.274° ( degrees), with a period of about 31.8 days. The evection in longitude is given by the expression +4586.45''\sin (2D-\ell), where D is the mean angular distance of the Moon from the Sun (its ''elongation''), and \ell is the mean angular distance of the Moon from its perigee (''mean anomaly''). It arises from an approximately six-monthly periodic variation of the eccentricity of the Moon's orbit and a libration of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equation Of The Centre
In two-body, Keplerian orbital mechanics, the equation of the center is the angular difference between the actual position of a body in its elliptical orbit and the position it would occupy if its motion were uniform, in a circular orbit of the same period. It is defined as the difference true anomaly, , minus mean anomaly, , and is typically expressed a function of mean anomaly, , and orbital eccentricity, . Discussion Since antiquity, the problem of predicting the motions of the heavenly bodies has been simplified by reducing it to one of a single body in orbit about another. In calculating the position of the body around its orbit, it is often convenient to begin by assuming circular motion. This first approximation is then simply a constant angular rate multiplied by an amount of time. However, the actual solution, assuming Newtonian physics, is an elliptical orbit (a Keplerian orbit). For these, it is easy to find the mean anomaly (and hence the time) for a given true anom ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kepler Orbit
In celestial mechanics, a Kepler orbit (or Keplerian orbit, named after the German astronomer Johannes Kepler) is the motion of one body relative to another, as an ellipse, parabola, or hyperbola, which forms a two-dimensional orbital plane in three-dimensional space. A Kepler orbit can also form a straight line. It considers only the point-like gravitational attraction of two bodies, neglecting perturbations due to gravitational interactions with other objects, atmospheric drag, solar radiation pressure, a non- spherical central body, and so on. It is thus said to be a solution of a special case of the two-body problem, known as the Kepler problem. As a theory in classical mechanics, it also does not take into account the effects of general relativity. Keplerian orbits can be parametrized into six orbital elements in various ways. In most applications, there is a large central body, the center of mass of which is assumed to be the center of mass of the entire system. B ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circle
A circle is a shape consisting of all point (geometry), points in a plane (mathematics), plane that are at a given distance from a given point, the Centre (geometry), centre. The distance between any point of the circle and the centre is called the radius. The length of a line segment connecting two points on the circle and passing through the centre is called the diameter. A circle bounds a region of the plane called a Disk (mathematics), disc. The circle has been known since before the beginning of recorded history. Natural circles are common, such as the full moon or a slice of round fruit. The circle is the basis for the wheel, which, with related inventions such as gears, makes much of modern machinery possible. In mathematics, the study of the circle has helped inspire the development of geometry, astronomy and calculus. Terminology * Annulus (mathematics), Annulus: a ring-shaped object, the region bounded by two concentric circles. * Circular arc, Arc: any Connected ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
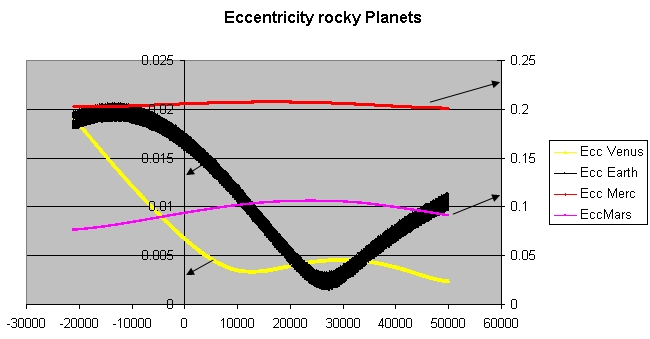
Eccentricity (orbit)
In astrodynamics, the orbital eccentricity of an astronomical object is a dimensionless parameter that determines the amount by which its orbit around another body deviates from a perfect circle. A value of 0 is a circular orbit, values between 0 and 1 form an elliptic orbit, 1 is a parabolic escape orbit (or capture orbit), and greater than 1 is a hyperbola. The term derives its name from the parameters of conic sections, as every Kepler orbit is a conic section. It is normally used for the isolated two-body problem, but extensions exist for objects following a rosette orbit through the Galaxy. Definition In a two-body problem with inverse-square-law force, every orbit is a Kepler orbit. The eccentricity of this Kepler orbit is a non-negative number that defines its shape. The eccentricity may take the following values: * Circular orbit: * Elliptic orbit: * Parabolic trajectory: * Hyperbolic trajectory: The eccentricity is given by e = \sqrt where is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree (angle)
A degree (in full, a degree of arc, arc degree, or arcdegree), usually denoted by ° (the degree symbol), is a measurement of a plane (mathematics), plane angle in which one Turn (geometry), full rotation is 360 degrees. It is not an SI unit—the SI unit of angular measure is the radian—but it is mentioned in the SI Brochure, SI brochure as an Non-SI units mentioned in the SI, accepted unit. Because a full rotation equals 2 radians, one degree is equivalent to radians. History The original motivation for choosing the degree as a unit of rotations and angles is unknown. One theory states that it is related to the fact that 360 is approximately the number of days in a year. Ancient astronomers noticed that the sun, which follows through the ecliptic path over the course of the year, seems to advance in its path by approximately one degree each day. Some ancient calendars, such as the Iranian calendar, Persian calendar and the Babylonian calendar, used 360 days for a year. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Synodic Month
In lunar calendars, a lunar month is the time between two successive Syzygy (astronomy), syzygies of the same type: new moons or full moons. The precise definition varies, especially for the beginning of the month. Variations In Shona people, Shona, Middle Eastern, and European traditions, the month starts when the new moon, young crescent moon first becomes visible, at evening, after Astronomical conjunction, conjunction with the Sun one or two days before that evening (e.g., in the Islamic calendar). In Egyptian calendar, ancient Egypt, the lunar month began on the day when the waning moon could no longer be seen just before sunrise. Others run from full moon to full moon. Yet others use calculation, of varying degrees of sophistication, for example, the Hebrew calendar, the Chinese calendar, or the Computus, ecclesiastical lunar calendar. Calendars count integer days, so months may be 29 or 30 days in length, in some regular or irregular sequence. Lunar Cycles, Lunar cycles ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Perturbation (astronomy)
In astronomy, perturbation is the complex motion of a massive body subjected to forces other than the gravitational attraction of a single other massive body. The other forces can include a third (fourth, fifth, etc.) body, resistance, as from an atmosphere, and the off-center attraction of an oblate or otherwise misshapen body. Introduction The study of perturbations began with the first attempts to predict planetary motions in the sky. In ancient times the causes were unknown. Isaac Newton, at the time he formulated his laws of motion and of gravitation, applied them to the first analysis of perturbations, recognizing the complex difficulties of their calculation. Many of the great mathematicians since then have given attention to the various problems involved; throughout the 18th and 19th centuries there was demand for accurate tables of the position of the Moon and planets for marine navigation. The complex motions of gravitational perturbations can be broken down. Th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |